湖南省益阳市沅江市2023-2024学年八年级下学期月考数学试题
试卷更新日期:2024-04-30 类型:月考试卷
一、选择题(共10小题,每小题3分,共30分,每小题只有一个选项是符合题意的)
-
1. 若式子在实数范围内有意义,则的取值范围是( )A、 B、 C、 D、2. 下列计算结果正确的是( )A、 B、 C、 D、3. 估算的值在( )A、0和1之间 B、1和2之间 C、2和3之间 D、3和4之间4. 104的绝对值是( )A、 B、 C、 D、1045. 2018年我市财政计划安排社会保障和公共卫生等支出约1800000000元支持民生幸福工程,数1800000000用科学记数法表示为A、 B、 C、 D、6. 下列图形既是轴对称图形,又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 7. 下列各式中,计算正确的是( )A、 B、 C、 D、8. 如图,已知 , 交于点 , , , 则的度数是( )
7. 下列各式中,计算正确的是( )A、 B、 C、 D、8. 如图,已知 , 交于点 , , , 则的度数是( ) A、 B、 C、 D、9. 沅江某中学足球队24名队员年龄情况如下:
A、 B、 C、 D、9. 沅江某中学足球队24名队员年龄情况如下:年龄(岁)
12
11
10
9
人数
4
10
8
2
则这个队队员年龄的众数和中位数分别是( )
A、11,10 B、11,11 C、10,9 D、10,1110. 对于反比例函数 ,下列说法不正确的是A、图象分布在第二、四象限 B、当 时, 随 的增大而增大 C、图象经过点(1,-2) D、若点 , 都在图象上,且 ,则二、填空题(共5小题,每小题3分,共15分)
-
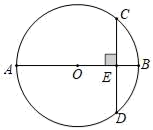
11. 计算: .12. 在一个不透明布袋里装有3个白球、2个红球和 个黄球,这些球除颜色不同其它没有任何区别.若从该布袋里任意摸出1个球,该球是黄球的概率为 ,则 等于 .13. 已知圆的半径是6,则圆内接正三角形的边长是 .14. 如图,AB为⊙O的直径,弦CD⊥AB于点E , 已知CD=8,EB=2,则⊙O的半径为 .
 15. 在平面直角坐标系中,抛物线的图象如图所示.已知A点坐标为 , 过点A作轴交抛物线于点 , 过点作交抛物线于点 , 过点作轴交抛物线于点 , 过点作交抛物线于点 , 依次进行下去,则点的坐标为 .
15. 在平面直角坐标系中,抛物线的图象如图所示.已知A点坐标为 , 过点A作轴交抛物线于点 , 过点作交抛物线于点 , 过点作轴交抛物线于点 , 过点作交抛物线于点 , 依次进行下去,则点的坐标为 .
三、解答题(共8小题,共75分.解答应写出过程)
-
16. 先化简,再求值: ,其中 .17. 如图,在由边长为1个单位长度的小正方形组成的网格中,有一条以格点(网格线的交点)为端点的线段 .
 (1)、线段的长为;(2)、请以线段为边在下图中作一个面积为26的矩形 , 要求点C,D均在格点上.18. 如图,在等腰中, , , 以斜边为一条直角边,向外作另一直角边长为1的 , 依次作下去,记的面积为 , 的面积为 , 的面积为 , …,回答下列问题:
(1)、线段的长为;(2)、请以线段为边在下图中作一个面积为26的矩形 , 要求点C,D均在格点上.18. 如图,在等腰中, , , 以斜边为一条直角边,向外作另一直角边长为1的 , 依次作下去,记的面积为 , 的面积为 , 的面积为 , …,回答下列问题: (1)、 , ;(2)、求的值.19. 某校为检测师生体温,在校门安装了某型号测温门.如图为该测温门截面示意图,已知测温门AD的顶部A处距地面高为2.2m,为了解自己的有效测温区间.身高1.6m的小聪做了如下实验:当他在地面N处时测温门开始显示额头温度,此时在额头B处测得A的仰角为18°;在地面M处时,测温门停止显示额头温度,此时在额头C处测得A的仰角为60°.求小聪在地面的有效测温区间MN的长度.(额头到地面的距离以身高计,计算精确到0.1m,sin18°≈0.31,cos18°≈0.95,tan18°≈0.32)
(1)、 , ;(2)、求的值.19. 某校为检测师生体温,在校门安装了某型号测温门.如图为该测温门截面示意图,已知测温门AD的顶部A处距地面高为2.2m,为了解自己的有效测温区间.身高1.6m的小聪做了如下实验:当他在地面N处时测温门开始显示额头温度,此时在额头B处测得A的仰角为18°;在地面M处时,测温门停止显示额头温度,此时在额头C处测得A的仰角为60°.求小聪在地面的有效测温区间MN的长度.(额头到地面的距离以身高计,计算精确到0.1m,sin18°≈0.31,cos18°≈0.95,tan18°≈0.32)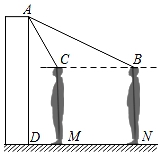 20. 如图,快递员小李从点出发,负责给三个菜鸟驿站派送包裹,站点位于点的北偏西方向上,站点位于点的南偏东方向上,站点位于点的北偏东方向上,且站点到点的距离与站点到点的距离相等.已知小李在派送包裹时,从点到站点所需要的时间分别为和 , 配送速度均为 .
20. 如图,快递员小李从点出发,负责给三个菜鸟驿站派送包裹,站点位于点的北偏西方向上,站点位于点的南偏东方向上,站点位于点的北偏东方向上,且站点到点的距离与站点到点的距离相等.已知小李在派送包裹时,从点到站点所需要的时间分别为和 , 配送速度均为 . (1)、试计算的度数;(2)、求站点与站点之间的距离.21. 如图,在中, , 分别是的中点,是线段上的点(不与重合),连接交于点 , 连接 .
(1)、试计算的度数;(2)、求站点与站点之间的距离.21. 如图,在中, , 分别是的中点,是线段上的点(不与重合),连接交于点 , 连接 . (1)、求证:四边形是菱形;(2)、求证:;(3)、当时,求的长.22. 已知两个全等的和 , a,b为直角边长(),为斜边长.
(1)、求证:四边形是菱形;(2)、求证:;(3)、当时,求的长.22. 已知两个全等的和 , a,b为直角边长(),为斜边长. (1)、将两个三角形按如图① 所示的位置(此时B,F重合)摆放,能够得到结论 . 下面是证明该结论的部分过程,请画出解图,并补充完整;
(1)、将两个三角形按如图① 所示的位置(此时B,F重合)摆放,能够得到结论 . 下面是证明该结论的部分过程,请画出解图,并补充完整;证明:如解图①,连接 , , 则 , …
(2)、利用如图②所示的和重新构造一个图形,并写出证明的过程.23. 已知四边形是菱形,直线经过点 , 且点右侧的部分在的下方,过点作于点 , 点是直线上一点且在点的右侧,连接 , . (1)、数学思考:
(1)、数学思考:如图①,当的边都在的右侧时,线段之间的数量关系为;
(2)、猜想证明:如图②,当的边分别在的两侧时,(1)中的结论是否依然成立?若成立,请给出证明;若不成立,请说明理由;
(3)、拓展延伸:若菱形的边长为13, , , 请直接写出线段的长.