四川省内江市隆昌市第一初级中学2023-2024学年九年级下学期第一次月考数学试题
试卷更新日期:2024-04-30 类型:月考试卷
一、选择题(本大题共12个小题,每小题3分,共36分。)
-
1. 的绝对值是( )A、 B、2024 C、 D、2. 据生物学可知,卵细胞是人体细胞中最大的细胞,其直径约为0.0002米.将数0.0002用科学记数法表示为( )A、 B、 C、 D、3. 下列图形中,既是中心对称图形又是轴对称图形的是( )A、等边三角形 B、平行四边形 C、矩形 D、正五边形4. 下列各式计算正确的是( )A、 B、 C、 D、5. 下列立体图形中,俯视图是三角形的是( )A、
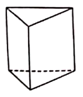 B、
B、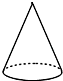 C、
C、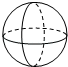 D、
D、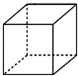 6. 在函数中,自变量的取值范围是( )A、且 B、且 C、 D、7. 已知一组数据5,4, ,3,9的平均数为5,则这组数据的中位数是( )A、3 B、4 C、5 D、68. 如图,在中,为上一点,连接 , 且交于点 , , 则( )
6. 在函数中,自变量的取值范围是( )A、且 B、且 C、 D、7. 已知一组数据5,4, ,3,9的平均数为5,则这组数据的中位数是( )A、3 B、4 C、5 D、68. 如图,在中,为上一点,连接 , 且交于点 , , 则( ) A、2:5 B、2:3 C、3:5 D、9. 某品牌服装折扣店将某件衣服按进价提高后标价,再打8折(标价的)销售,售价为240元。设这件衣服的进价为元,根据题意,下面所列的方程正确的是( )A、 B、 C、 D、10. 如图,AB是 的直径,弦 , , ,则阴影部分的面积为( )
A、2:5 B、2:3 C、3:5 D、9. 某品牌服装折扣店将某件衣服按进价提高后标价,再打8折(标价的)销售,售价为240元。设这件衣服的进价为元,根据题意,下面所列的方程正确的是( )A、 B、 C、 D、10. 如图,AB是 的直径,弦 , , ,则阴影部分的面积为( ) A、 B、 C、 D、11. 如图,反比例函数的图象经过矩形对角线的交点 , 分别于交于点 , 若四边形的面积为12,则的值为( )
A、 B、 C、 D、11. 如图,反比例函数的图象经过矩形对角线的交点 , 分别于交于点 , 若四边形的面积为12,则的值为( ) A、2 B、3 C、4 D、512. 如图,抛物线的对称轴为直线 , 与轴的一个交点坐标为 , 其部分图象如图所示,下列结论:
A、2 B、3 C、4 D、512. 如图,抛物线的对称轴为直线 , 与轴的一个交点坐标为 , 其部分图象如图所示,下列结论:
;方程的两个根是 , ;;
当时,的取值范围是;当时,随增大而增大.
其中结论正确的个数是( )
A、4个 B、3个 C、2个 D、1个二、填空题(本大题共4小题,每小题5分,共20分、请将最后答案直接填在题中横线上。)
-
13. 分解因式: =14. 在如图所示的四边形中,若去掉一个的角得到一个五边形,则;
 15. 若关于的一元二次方程有不相等实数根,则的取值范围是;16. 如图,在等边中,为边上一点,为边上一点,且 , , , 则等边的边长为 .
15. 若关于的一元二次方程有不相等实数根,则的取值范围是;16. 如图,在等边中,为边上一点,为边上一点,且 , , , 则等边的边长为 .
三、解答题(本大题共5个小题,共44分、解答题必须写出必要的文字说明、证明过程或推演步骤。)
-
17. 计算:18. 在中,点在对角线上,且 ,

求证:
(1)、;(2)、四边形是平行四边形。19. 为推广阳光体育“大课间”活动,我市某中学决定在学生中开设A:实心球,B:立定跳远,C:跳绳,D:跑步四种活动项目.为了了解学生对四种项目的喜欢情况,随机抽取了部分学生进行调查,并将调查结果绘制成如图①②的统计图.请结合图中的信息解答下列问题: (1)、在这项调查中,共调查了多少名学生?(2)、请计算本项调查中喜欢“立定跳远”的学生人数和所占百分比,并将两个统计图补充完整;(3)、若调查到喜欢“跳绳”的5名学生中有3名男生,2名女生.现从这5名学生中任意抽取2名学生.请用画树状图或列表的方法,求出刚好抽到同性别学生的概率.20. 为建设“宜居宜业宜游”山水园林式城市,内江市正在对城区沱江河段进行区域性景观打造。如图,某施工单位为测得某河段的宽度,测量员先在河对岸边取一点 , 再在河这边沿河边取两点 , 在点处测得点在北偏东方向上,在点处测得点在西北方向上,量得长为200米。请你求出该河段的宽度(结果保留根号)。
(1)、在这项调查中,共调查了多少名学生?(2)、请计算本项调查中喜欢“立定跳远”的学生人数和所占百分比,并将两个统计图补充完整;(3)、若调查到喜欢“跳绳”的5名学生中有3名男生,2名女生.现从这5名学生中任意抽取2名学生.请用画树状图或列表的方法,求出刚好抽到同性别学生的概率.20. 为建设“宜居宜业宜游”山水园林式城市,内江市正在对城区沱江河段进行区域性景观打造。如图,某施工单位为测得某河段的宽度,测量员先在河对岸边取一点 , 再在河这边沿河边取两点 , 在点处测得点在北偏东方向上,在点处测得点在西北方向上,量得长为200米。请你求出该河段的宽度(结果保留根号)。 21. 如图,一次函数与反比例函数的图象交于 , 两点。
21. 如图,一次函数与反比例函数的图象交于 , 两点。 (1)、求反比例函数和一次函数的解析式;(2)、连接 , 求的面积(3)、点是轴上的一动点,要使最小,试求出点的坐标。
(1)、求反比例函数和一次函数的解析式;(2)、连接 , 求的面积(3)、点是轴上的一动点,要使最小,试求出点的坐标。四、填空题(本大题共4小题,每小题6分,共24分。)
-
22. 已知 + =3,则代数式 的值为 .23. 如图,已知直线 , 过点作轴的垂线交直线于点 , 过点作直线的垂线交轴于点;过点作轴的垂线交直线于 , 过点作直线的垂线交轴于点;按此作法继续下去,则点的坐标为;
 24. 关于的不等式组恰好有3个整数解,则的取值范围是;25. 如图,在等腰中, , , 点在边上, , 点在边上, , 垂足为 , 则的长为 .
24. 关于的不等式组恰好有3个整数解,则的取值范围是;25. 如图,在等腰中, , , 点在边上, , 点在边上, , 垂足为 , 则的长为 .
五、解答题(本大题共3个小题,每小题12分,共36分。解答题必须写出必要的文字说明、证明过程或推演步骤。)
-
26. 如图,在中,点在斜边上,以为直径的与相切于点
 (1)、求证:平分(2)、若①求的值;②求图中阴影部分的面积.27. 一家蔬菜公司收购到某种绿色蔬菜140吨,准备加工后进行销售,销售后获利的情况如下表所示:
(1)、求证:平分(2)、若①求的值;②求图中阴影部分的面积.27. 一家蔬菜公司收购到某种绿色蔬菜140吨,准备加工后进行销售,销售后获利的情况如下表所示:销售方式
粗加工后销售
精加工后销售
每吨获利(元)
1000
2000
已知该公司的加工能力是:每天能精加工5吨或粗加工15吨,但两种加工不能同时进行。受季节等条件的限制,公司必须在一定时间内将这批蔬菜全部加工后销售完。
(1)、如果要求12天刚好加工完140吨蔬菜,则公司应安排几天精加工,几天粗加工?(2)、如果先进行精加工,然后进行粗加工。①试求出销售利润元与精加工的蔬菜吨数之间的函数关系式;
②若要求在不超过10天的时间内,将140吨蔬菜全部加工完后进行销售,则加工这批蔬菜最多获得多少利润?此时如何分配加工时间?
28. 如图,已知抛物线的对称轴为 , 且抛物线经过两点,与轴交于点 (1)、求抛物线的解析式;(2)、在第二象限抛物线上找一点 , 的面积最大,求出此点的坐标;(3)、设点为抛物线的对称轴上的一个动点,求使为直角三角形的点的坐标。
(1)、求抛物线的解析式;(2)、在第二象限抛物线上找一点 , 的面积最大,求出此点的坐标;(3)、设点为抛物线的对称轴上的一个动点,求使为直角三角形的点的坐标。