四川省雅安市2024年中考一诊数学模拟试题

试卷更新日期：2024-04-30 类型：中考模拟

进入出卷网下载

一、选择题（每小题3分，共36分）

1. $- 2024$ 的绝对值是（）

A、2024 B、 $- 2024$ C、 $\frac{1}{2024}$ D、 $- \frac{1}{2024}$

查看试题解析
2. 风云二号是我国自行研制的第一代地球静止气象卫星，它在地球赤道上空距地面约35800公里的轨道上运行．将35800用科学记数法表示应为（）

A、 $0.358 \times 1 0^{5}$ B、 $35.8 \times 1 0^{3}$ C、 $3.58 \times 1 0^{5}$ D、 $3.58 \times 1 0^{4}$

查看试题解析
3. 在平面直角坐标系中，点 $A (2, - 8)$ 和点 $B$ 关于 $y$ 轴对称，则点 $B$ 的坐标是（）

A、 $(- 2, - 8)$ B、 $(2, 8)$ C、 $(- 2, 8)$ D、 $(8, 2)$

查看试题解析
4. 下列计算正确的是（）

A、 $a^{5} + a^{3} = a^{8}$ B、 $2 a^{2} + 3 a^{2} = 5 a^{4}$ C、 $(a b)^{2} = a^{2} b^{2}$ D、 $a^{6} \div a^{2} = a^{3}$

查看试题解析
5. 若分式 $\frac{x^{2} - 1}{x - 1}$ 的值为0，则x的值为（）

A、1 B、 $- 1$ C、0 D、 $\pm 1$

查看试题解析
6. 如图，在四边形ABCD中， $∠ A B C = 90 °$ ，点E、F分别是AC、AD的中点，且 $B E = E F$ ，若 $A B = 8$ ， $B C = 4$ ，则CD的长为（）

A、 $4 \sqrt{5}$ B、 $4 \sqrt{3}$ C、 $2 \sqrt{5}$ D、8

查看试题解析
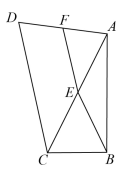7. 某立方体的主视图如图所示，它的左视图不可能是（）

A、 B、 C、 D、

查看试题解析
8. 下列说法中，正确的是（）

A、对载人航天器零部件的检查适合采用抽样调查 B、某种彩票中奖的概率是 $\frac{1}{10}$ ，则购买10张这种彩票一定会中奖 C、为了了解一批洗衣粉的质量情况，从仓库中随机抽取100袋洗衣粉进行检验，这个问题中的样本是100 D、甲．乙两人各进行了10次射击测试，他们的平均成绩相同，方差分别是 $S_{甲}^{2} = 3.2, S_{乙}^{2} = 1$ ，则乙的射击成绩较稳定

查看试题解析
9. 已知直角三角形的两条边长分别是方程 $x^{2} - 9 x + 20 = 0$ 的两个根，则此三角形的第三边是（）

A、4或5 B、3 C、 $\sqrt{41}$ D、3或 $\sqrt{41}$

查看试题解析
10. 杭州第19届亚运会会徽名为“潮涌”，会徽主体图形由扇面、钱塘江、钱江潮头、赛道、互联网符号及象征亚奥理事会的太阳图形六个元素组成，下方是主办城市名称与举办年份的印鉴，两者共同构成了完整的杭州亚运会会徽．小王同学在制作亚运会手抄报时，绘制了如图的扇面示意图，扇面弧所对的圆心角为 $120 °$ ，大扇形半径为 $10 c m$ ，小扇形半径为 $3 c m$ ，则此扇面中阴影部分的面积是（）

A、 $\frac{91}{3} π c m^{2}$ B、 $\frac{86}{3} π c m^{2}$ C、 $\frac{70}{3} π c m^{2}$ D、 $\frac{65}{3} π c m^{2}$

查看试题解析
11. 如图，四边形ABCD内接于 $⊙ O$ ，若四边形ABCO是菱形，则 $∠ D$ 的度数为（）

A、45° B、60° C、90° D、120°

查看试题解析
12. 如图是二次函数 $y = a x^{2} + b x + c$ （ $a, b, c$ 是常数， $a \neq 0$ ）图象的一部分，与 $x$ 轴的交点 $A$ 在点 $(2, 0)$ 和 $(3, 0)$ 之间，对称轴是直线 $x = 1$ ．对于下列说法：① $a b < 0$ ；② $2 a + b = 0$ ；③ $3 a + c > 0$ ；④ $a + b \geq m (a m + b)$ （ $m$ 为实数），其中正确的是（）

A、①②④ B、①② C、②③④ D、③④

查看试题解析

二、填空题（每小题3分，共15分）

13. 一组数据1，6，7，4，7，5，2的中位数是．

查看试题解析
14. 若 $x_{1}, x_{2}$ 是方程 $x^{2} - x - 2023 = 0$ 的两个实数根，则代数式 $x_{1}^{2} + x_{2}$ 的值为．

查看试题解析
15. 若正 $n$ 边形的一个内角是 $140 °$ ，那么它的边数 $n =$ ．

查看试题解析
16. 如图，在 $△ A B C$ 中， $∠ C = 90 ° ， A C = B C = 6$ ． P为边 $A B$ 上一动点，作 $P D ⊥ B C$ 于点D， $P E ⊥ A C$ 于点E，则 $D E$ 的最小值为．

查看试题解析
17. 如图，正方形 $A B C D$ ，点 $F$ 在边 $A B$ 上，且 $A F : F B = 1 : 2$ ， $C E ⊥ D F$ ，垂足为 $M$ ，且交 $A D$ 于点 $E, A C$ 与 $D F$ 交于点 $N$ ，延长 $C B$ 至 $G$ ，使 $B G = \frac{1}{2} B C$ ，连接 $G M$ ，有如下结论：① $D E = A F$ ；② $A N = \frac{\sqrt{2}}{4} A B$ ；③ $∠ A D F = ∠ G M F$ ；④ $S_{△ A N F} : \cdot S_{四边形 C N F B} = 1 : 8$ ．
上述结论中，所有正确结论的序号是．

查看试题解析

三、解答题（本大题共7个小题，共69分）

18.

(1)、计算： ${(\frac{1}{2})}^{- 2} - (π - 3)^{0} + | \sqrt{3} - 2 | + 2 s i n 60 °$ ；

(2)、先化简，再求值： $(\frac{x + 1}{x - 2} - 1) \div \frac{x^{2} - 2 x}{x^{2} - 4 x + 4}$ ，其中整数 $x$ 与2，3构成 $△ A B C$ 的三条边长，请求出所有满足条件的代数式的值．

查看试题解析
19. 为了倡导“节约用水，从我做起”，某社区决定对该辖区200户家庭用水情况进行调查，调查小组随机抽查了其中部分家庭一年的月平均用水量（单位：吨），调查中发现，每户家庭月平均用水量在3~7吨范围内，并将调查结果制成了如下尚不完整的统计表：
月平均用水量（吨）
3
4
5
6
7
频数（户数）
4
$a$
9
10
7
频率
0.08
0.40
$b$
$c$
0.14
请根据统计表中提供的信息解答下列问题：

(1)、填空： $a =$ ， $b =$ ， $c =$ ．

(2)、根据样本数据，估计该辖区200户家庭中月平均用水量不超过5吨的约有多少户？

(3)、该社区决定从月平均用水量最省的甲、乙、丙、丁四户家庭中，选取两户进行“节水”经验分享．请用列表或画树状图的方法，求出恰好选到甲、丙两户的概率．

查看试题解析
20. 某超市销售一种商品，成本价为30元/千克，经市场调查，每天销售量 $y$ （千克）与销售单价 $x$ （元/千克）之间的关系如图所示，规定每千克售价不能低于30元，且不高于80元．

(1)、直接写出 $y$ 与 $x$ 之间的函数关系式；

(2)、如果该超市销售这种商品每天获得3600元的利润，那么该商品的销售单价为多少元？

(3)、设每天的总利润为 $w$ 元，当销售单价定为多少元时，该超市每天的利润最大？最大利润是多少元？

查看试题解析
21. 如图，在 $▱ A B C D$ 中， $O$ 是对角线 $A C 、 B D$ 的交点， $B E ⊥ A C, D F ⊥ A C$ ，垂足分别为点 $E 、 F$ ．

(1)、求证： $A F = C E$ ．

(2)、若 $D B = 20, O E = 6$ ，求 $t a n ∠ O D F$ 的值．

查看试题解析
22. 如图，平面直角坐标系中，函数 $y = \frac{k}{x}$ 的图象上 $A 、 B$ 两点的坐标分别为 $A (n, n + 1), B (n - 5, - 2 n)$ ．

(1)、求反比例函数 $y = \frac{k}{x}$ 和直线 $A B$ 的表达式；

(2)、连接 $A O 、 B O$ ，求 $△ A O B$ 的面积．

查看试题解析
23. 如图， $A B$ 是 $⊙ O$ 的直径，点 $C, D$ 在 $⊙ O$ 上， $A D$ 平分 $∠ C A B$ ，过点 $D$ 作 $A C$ 的垂线交 $A C$ 的延长线于点 $E$ ，交 $A B$ 的延长线于点 $F$ ，连接 $B D$ ．

(1)、求证： $E F$ 是 $⊙ O$ 的切线；

(2)、求证： $A B \cdot (A B - A E) = A C \cdot B F$

(3)、若 $A B = 10, A C = 6$ ，求 $A D$ 的长．

查看试题解析
24. 已知二次函数 $y = x^{2} + b x + c$ 图象 $C_{1}$ 交 $x$ 轴于点 $(- 1, 0)$ 和 $(3, 0)$ 两点；

(1)、求抛物线的解析式；

(2)、将抛物线 $C_{1}$ 向上平移 $n$ 个单位得抛物线 $C_{2}$ ，点 $P$ 为抛物线 $C_{2}$ 的顶点， $C (0, 4)$ ，过 $C$ 点作 $x$ 轴的平行线交抛物线 $C_{2}$ 于点 $A$ ，点 $B$ 为 $y$ 轴上的一动点，若存在 $∠ A B P = 90 °$ 有且只有一种情况，求此时 $n$ 的值；

(3)、如图2，恒过定点 $(1, 1)$ 的直线 $Q N$ 交抛物线 $C_{1}$ 于点 $Q, N$ 两点，过 $Q$ 点的直线 $y = - 2 x + t$ 的直线交抛物线 $C_{1}$ 于 $M$ 点，作直线 $M N$ ，求 $M N$ 恒过的定点坐标．

查看试题解析

月平均用水量（吨）	3	4	5	6	7
频数（户数）	4	$a$	9	10	7
频率	0.08	0.40	$b$	$c$	0.14