四川省内江市隆昌市知行中学2023-2024学年九年级下学期第一次月考数学试题
试卷更新日期:2024-04-30 类型:月考试卷
一、选择题(本大题共12个小题,每小题3分,共36分。)
-
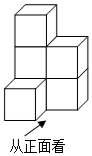
1. 的相反数是( )A、 B、2024 C、 D、2. 已知某细菌直径长约0.0000152米,那么该细菌的直径长用科学记数法可表示为( )A、米 B、米 C、米 D、米3. 如图,几何体由6个大小相同的正方体组成,其左视图是( )
 A、
A、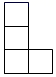 B、
B、 C、
C、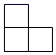 D、
D、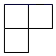 4. 下列计算正确的是( )A、 B、 C、 D、5. 函数的自变量取值范围是( )A、 B、 C、 D、6. 如图,四个图标中是轴对称图形的是( )A、
4. 下列计算正确的是( )A、 B、 C、 D、5. 函数的自变量取值范围是( )A、 B、 C、 D、6. 如图,四个图标中是轴对称图形的是( )A、 B、
B、 C、
C、 D、
D、 7. 甲,乙两人练习跑步,若乙先跑10米,则甲跑5秒就可以追上乙;若乙先跑2秒,则甲跑4秒就可追上乙.若设甲的速度为x米/秒,乙的速度为y米/秒,则下列方程组中正确的是( )A、 B、 C、 D、8. 若与相似且对应中线之比为 , 则周长之比和面积比分别是( )A、 , B、 , C、 , D、 ,9. 今年我市有近9600名考生参加中考,为了解这些考生的数学成绩,从中抽取600名考生的数学成绩进行统计分析,这个问题中样本是( )A、每位考生的数学成绩 B、9600名考生的数学成绩 C、被抽取的600名考生的数学成绩 D、被抽取的600名学生10. 如图,是某供水管道的截面图,里面尚有一些水,若液面宽度 , 半径于D,液面深度 , 则该管道的半径长为( )
7. 甲,乙两人练习跑步,若乙先跑10米,则甲跑5秒就可以追上乙;若乙先跑2秒,则甲跑4秒就可追上乙.若设甲的速度为x米/秒,乙的速度为y米/秒,则下列方程组中正确的是( )A、 B、 C、 D、8. 若与相似且对应中线之比为 , 则周长之比和面积比分别是( )A、 , B、 , C、 , D、 ,9. 今年我市有近9600名考生参加中考,为了解这些考生的数学成绩,从中抽取600名考生的数学成绩进行统计分析,这个问题中样本是( )A、每位考生的数学成绩 B、9600名考生的数学成绩 C、被抽取的600名考生的数学成绩 D、被抽取的600名学生10. 如图,是某供水管道的截面图,里面尚有一些水,若液面宽度 , 半径于D,液面深度 , 则该管道的半径长为( ) A、6Cm B、5.5Cm C、5Cm D、4Cm11. 如图,若 , 则、、之间关系是( )
A、6Cm B、5.5Cm C、5Cm D、4Cm11. 如图,若 , 则、、之间关系是( ) A、 B、 C、 D、12. 如图,在正方形ABCD中,是等边三角形,BP、CP的延长线分别交AD于点E、F , 连接BD、DP , BD与CF相交于点H , 给出下列结论:①;②∽;③∽;④ , 其中正确的是( )
A、 B、 C、 D、12. 如图,在正方形ABCD中,是等边三角形,BP、CP的延长线分别交AD于点E、F , 连接BD、DP , BD与CF相交于点H , 给出下列结论:①;②∽;③∽;④ , 其中正确的是( ) A、①②③④ B、②③ C、①②④ D、①③④
A、①②③④ B、②③ C、①②④ D、①③④二、填空题(本大题共4小题,每小题5分,共20分。)
-
13. 分解因式:;14. 关于x的方程有实数根,则偶数m的最大值为;15. 将一矩形纸条按下图所示折叠,若 , 则∠2=°;
 16. 如图矩形ABCD中, , , 连接AC , 将线段AC、AB分别绕点A顺时针旋转90°至AE、AF , 线段AE与弧BF交于点G , 连接CG , 则图中阴影部分面积为 .
16. 如图矩形ABCD中, , , 连接AC , 将线段AC、AB分别绕点A顺时针旋转90°至AE、AF , 线段AE与弧BF交于点G , 连接CG , 则图中阴影部分面积为 .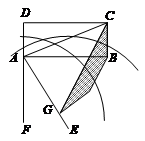
三、解答题(本大题共5小题,共44分。解答应写出必要的文字说明或推演步骤)
-
17. 计算:18. 如图,分别以的直角边AC及斜边AB向外作等边及等边 , 已知: , , 垂足为F , 连接DF
 (1)、试说明;(2)、求证:四边形ADFE是平行四边形。19. 在大课间活动中,同学们积极参加体育锻炼,小明就本班同学“我最喜爱的体育项目”进行了一次调查统计,下面是他通过收集数据后,绘制的两幅不完整的统计图.请你根据图中提供的信息,解答以下问题:
(1)、试说明;(2)、求证:四边形ADFE是平行四边形。19. 在大课间活动中,同学们积极参加体育锻炼,小明就本班同学“我最喜爱的体育项目”进行了一次调查统计,下面是他通过收集数据后,绘制的两幅不完整的统计图.请你根据图中提供的信息,解答以下问题: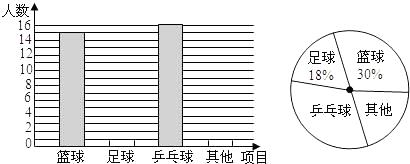 (1)、该班共有名学生;(2)、补全条形统计图;(3)、在扇形统计图中,“乒乓球”部分所对应的圆心角度数为;(4)、学校将举办体育节,该班将推选5位同学参加乒乓球活动,有3位男同学(A,B,C)和2位女同学(D,E),现准备从中选取两名同学组成双打组合,用树状图或列表法求恰好选出一男一女组成混合双打组合的概率.20. 小明同学在综合实践活动中对本地的一座古塔进行了测量.如图,他在山坡坡脚P处测得古塔顶端M的仰角为 ,沿山坡向上走25m到达D处,测得古塔顶端M的仰角为 .已知山坡坡度 ,即 ,请你帮助小明计算古塔的高度ME.(结果精确到0.1m,参考数据: )
(1)、该班共有名学生;(2)、补全条形统计图;(3)、在扇形统计图中,“乒乓球”部分所对应的圆心角度数为;(4)、学校将举办体育节,该班将推选5位同学参加乒乓球活动,有3位男同学(A,B,C)和2位女同学(D,E),现准备从中选取两名同学组成双打组合,用树状图或列表法求恰好选出一男一女组成混合双打组合的概率.20. 小明同学在综合实践活动中对本地的一座古塔进行了测量.如图,他在山坡坡脚P处测得古塔顶端M的仰角为 ,沿山坡向上走25m到达D处,测得古塔顶端M的仰角为 .已知山坡坡度 ,即 ,请你帮助小明计算古塔的高度ME.(结果精确到0.1m,参考数据: ) 21. 如图,反比例函数的图像与一次函数的图像在第一象限内相交于点A(4,n)
21. 如图,反比例函数的图像与一次函数的图像在第一象限内相交于点A(4,n)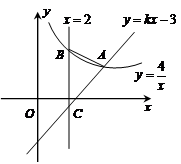 (1)、求n的值及一次函数的解析式;(2)、直线与反比例函数和一次函数的图象分别交于点B、C , 求的面积。
(1)、求n的值及一次函数的解析式;(2)、直线与反比例函数和一次函数的图象分别交于点B、C , 求的面积。四、填空题(本大题共4小题,每小题6分,共24分。)
-
22. 已知 , 则;23. 在梯形ABCD中, , E , F分别是边AB , CD的中点,如果 , , 那么;24. 对于实数 , 规定 , 例如 , , 那么计算
的结果是;
25. 如图,四条直线 , , , , , 过点作轴交于点 , 再过点作 , 交于点 , 再过点作交y轴于点 , ……,则点的坐标为.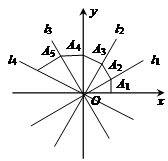
五、解答题(本大题共3个小题,每小题12分,共36分。解答题必须写出必要的文字说明、证明过程或推演步骤)
-
26. 为支持国家南水北调工程建设,小王家由原来养殖户变为种植户,经市场调查得知,当种植樱桃的面积x不超过15亩时,每亩可获得利润y=1900元;超过15亩时,每亩获得利润y(元)与种植面积x(亩)之间的函数关系如下表(为所学过的一次函数,反比例函数或二次函数中的一种)
x(亩)
20
25
30
35
y(元)
1800
1700
1600
1500
(1)、请求出种植樱桃的面积超过15亩时每亩获得利润y与x的函数关系式;(2)、如果小王家计划承包荒山种植樱桃,受条件限制种植樱桃面积x不超过50亩,设小王家种植x亩樱桃所获得的总利润为W元,求小王家承包多少亩荒山获得的总利润最大,并求总利润W(元)的最大值.27. 如图,AB是⊙O的直径,C是⊙O上一点,过点O作OD⊥AB,交BC的延长线于D,交AC于点E,F是DE的中点,连接CF.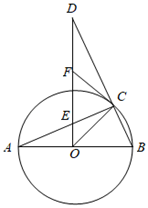 (1)、求证:CF是⊙O的切线.(2)、若∠A=22.5°,求证:AC=DC.28. 如图,抛物线与x轴交于点A( , 0)和点B(4,0),与y轴交于点C , 顶点为D , 连接AC , BC , BC与抛物线的对称轴l交于点E
(1)、求证:CF是⊙O的切线.(2)、若∠A=22.5°,求证:AC=DC.28. 如图,抛物线与x轴交于点A( , 0)和点B(4,0),与y轴交于点C , 顶点为D , 连接AC , BC , BC与抛物线的对称轴l交于点E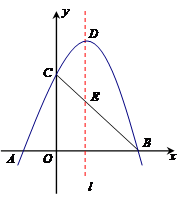 (1)、求抛物线的表达式;(2)、点P是第一象限内抛物线上的动点,连接PB , PC , 若 , 求点P的坐标;(3)、点N是对称轴l右侧抛物线上的动点,在射线ED上是否存在点M , 使得以点M , N , E为顶点的三角形与相似?若存在,直接写出点M的坐标;若不存在,说明理由。
(1)、求抛物线的表达式;(2)、点P是第一象限内抛物线上的动点,连接PB , PC , 若 , 求点P的坐标;(3)、点N是对称轴l右侧抛物线上的动点,在射线ED上是否存在点M , 使得以点M , N , E为顶点的三角形与相似?若存在,直接写出点M的坐标;若不存在,说明理由。