四川省攀枝花市仁和区2024年中考一模数学模拟试题
试卷更新日期:2024-04-30 类型:中考模拟
一、选择题:(本大题共12个小题,每小题5分,共60分.)
-
1. 的平方根是( )A、 B、 C、 D、2. 下列计算正确的是( )A、 B、 C、 D、3. 如图所示的几何体,该几何体的俯视图是( )
 A、
A、 B、
B、 C、
C、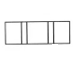 D、
D、 4. 清代诗人袁枚创作了一首诗《苔》:“白日不到处,青春恰自来.苔花如米小,也学牡丹开.”歌颂了苔在恶劣环境下仍有自己的生命意向.若苔花的花粉粒的直径约为米,将用科学记数法表示为( )A、 B、 C、 D、5. 下列说法错误的是( )A、矩形是轴对称图形 B、一个菱形的内角和为 C、调查乘坐飞机的旅客是否携带了违禁物品,应采用全面调查的方式 D、如果某彩票的中奖概率是 , 那么一次购买张这种彩票一定会中奖6. 已知点A的坐标为 , 直线轴,且 , 则点B的坐标为( )A、或 B、或 C、或 D、或7. 在锐角中, , 则( )A、30° B、45° C、60° D、75°8. 如图,正方形网格中,点A , O , B , E均在格点上.过点A , E且与交于点C , 点D是上一点,则( ).
4. 清代诗人袁枚创作了一首诗《苔》:“白日不到处,青春恰自来.苔花如米小,也学牡丹开.”歌颂了苔在恶劣环境下仍有自己的生命意向.若苔花的花粉粒的直径约为米,将用科学记数法表示为( )A、 B、 C、 D、5. 下列说法错误的是( )A、矩形是轴对称图形 B、一个菱形的内角和为 C、调查乘坐飞机的旅客是否携带了违禁物品,应采用全面调查的方式 D、如果某彩票的中奖概率是 , 那么一次购买张这种彩票一定会中奖6. 已知点A的坐标为 , 直线轴,且 , 则点B的坐标为( )A、或 B、或 C、或 D、或7. 在锐角中, , 则( )A、30° B、45° C、60° D、75°8. 如图,正方形网格中,点A , O , B , E均在格点上.过点A , E且与交于点C , 点D是上一点,则( ). A、 B、2 C、 D、9. 随着5G网络技术的发展,市场对5G产品的需求越来越大,为满足市场需求,某大型5G产品生产厂家更新技术后,加快了生产速度,现在平均每天比更新技术前多生产30万件产品,现在生产500万件产品所需的时间与更新技术前生产400万件产品所需时间相同,设更新技术前每天生产x万件,依据题意得( )A、 B、 C、 D、10. 如图,将半径为的圆形纸片沿折叠后,圆弧恰好能经过圆心 , 用图中阴影部分的扇形围成一个圆锥的侧面,则这个圆锥的高为( )
A、 B、2 C、 D、9. 随着5G网络技术的发展,市场对5G产品的需求越来越大,为满足市场需求,某大型5G产品生产厂家更新技术后,加快了生产速度,现在平均每天比更新技术前多生产30万件产品,现在生产500万件产品所需的时间与更新技术前生产400万件产品所需时间相同,设更新技术前每天生产x万件,依据题意得( )A、 B、 C、 D、10. 如图,将半径为的圆形纸片沿折叠后,圆弧恰好能经过圆心 , 用图中阴影部分的扇形围成一个圆锥的侧面,则这个圆锥的高为( ) A、 B、 C、 D、11. 如图,在中, , . ①分别以点、为圆心,大于的长为半径作弧,两弧相交于点、 , 作直线 , 交于点 , 连接;②以点为圆心,任意长为半径作弧,分别交、于点、 , 再分别以点、为圆心,大于的长为半径作弧,两弧相交于点 , 作射线 , 交线段于点 . 根据以上信息推断,下列结论错误的是( )
A、 B、 C、 D、11. 如图,在中, , . ①分别以点、为圆心,大于的长为半径作弧,两弧相交于点、 , 作直线 , 交于点 , 连接;②以点为圆心,任意长为半径作弧,分别交、于点、 , 再分别以点、为圆心,大于的长为半径作弧,两弧相交于点 , 作射线 , 交线段于点 . 根据以上信息推断,下列结论错误的是( ) A、 B、 C、 D、12. 如图,在中, , , , 点P从点A出发沿的路径运动到点C停止,点Q以相同的速度沿的路径运动到点C停止,连接 , 设点P的运动路程为x,的面积为y,则下列图象能大致反映y与x之间的函数关系的是( )
A、 B、 C、 D、12. 如图,在中, , , , 点P从点A出发沿的路径运动到点C停止,点Q以相同的速度沿的路径运动到点C停止,连接 , 设点P的运动路程为x,的面积为y,则下列图象能大致反映y与x之间的函数关系的是( )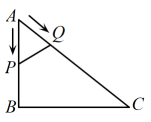 A、
A、 B、
B、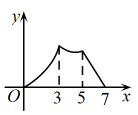 C、
C、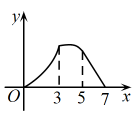 D、
D、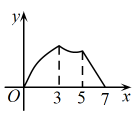
二、填空题:(本大题共4小题,每小题5分,共20分)
-
13. 因式分解: .14. 如图,在中,点、、分别在、、上,且 , , , 若 , 则的长为 .
 15. 如图,我海军舰艇在某海域C岛附近巡航,计划从A岛向北偏东方向的B岛直线行驶.测得C岛在A岛的北偏东方向,在B岛的北偏西方向.A , B之间的距离为海里,则C岛到航线的最短距离是海里.
15. 如图,我海军舰艇在某海域C岛附近巡航,计划从A岛向北偏东方向的B岛直线行驶.测得C岛在A岛的北偏东方向,在B岛的北偏西方向.A , B之间的距离为海里,则C岛到航线的最短距离是海里. 16. 如图,在正方形 中,点E是边 的中点,连接 、 ,分别交 、 于点P、Q , 过点P作 交 的延长线于F , 下列结论:
16. 如图,在正方形 中,点E是边 的中点,连接 、 ,分别交 、 于点P、Q , 过点P作 交 的延长线于F , 下列结论:① ,② ,③ ,④若四边形 的面积为4,则该正方形 的面积为36,⑤ .
其中正确的结论有 .

三、解答题:(本大题共8小题,共70分.解答应写出文字说明、证明过程或演算步骤.)
-
17. 解不等式组: , 并把解集在数轴上表示出来.18. 已知:如图,在中, , 点D是的中点,点E是的中点,过点C作交的延长线于点F .
 (1)、求证:四边形是平行四边形;(2)、若 , , 求的长.19. 某校为加强书法教学,了解学生现有的书写能力,随机抽取了部分学生进行测试,测试结果分为优秀、良好、及格、不及格四个等级,分别用A , B , C , D表示,并将测试结果绘制成两幅不完整的统计图.
(1)、求证:四边形是平行四边形;(2)、若 , , 求的长.19. 某校为加强书法教学,了解学生现有的书写能力,随机抽取了部分学生进行测试,测试结果分为优秀、良好、及格、不及格四个等级,分别用A , B , C , D表示,并将测试结果绘制成两幅不完整的统计图.
请根据统计图中的信息解答以下问题;
(1)、本次抽取的学生共有 ▲ 人,扇形统计图中A所对应扇形的圆心角是 ▲ , 并把条形统计图补充完整;(2)、依次将优秀、良好、及格、不及格记为90分、80分、70分、50分,则抽取的这部分学生书写成绩的众数是分,中位数是分,平均数是分;(3)、A等级的4名学生中有3名女生和1名男生,现在需要从这4人中随机抽取2人参加电视台举办的“中学生书法比赛”,请用列表或画树状图的方法,求被抽取的2人恰好是1名男生1名女生的概率.20. 暖暖花城攀枝花,不仅阳光充沛,特色水果更是闻名全国,某经销商计划购进A、B两种水果.已知购进A种水果2件,B种水果3件,共需690元;购进A种水果1件,B种水果4件,共需720元.(1)、A、B两种水果每件的价格分别是多少元?(2)、该经销商计划用不超过5400元购进A、B两种水果共40件,且A种水果的件数不超过B种水果件数的3倍,共有多少种进货方案?如果该经销商将购进的水果按照A种每件160元,B种每件200元的价格全部售出,那么哪种进货方案获利最多?21. 如图,一次函数的图象与反比例函数的图象交于点 , 与y轴交于点B . (1)、求a , k的值;(2)、直线过点A , 与反比例函数图象交于点C , 与x轴交于点D , , 连接 .
(1)、求a , k的值;(2)、直线过点A , 与反比例函数图象交于点C , 与x轴交于点D , , 连接 .①求的面积;
②直接写出不等式的解集.
22. 如图,AB为⊙O的直径,D、E是⊙O上的两点,延长AB至点C,连接CD,∠BDC=∠BAD. (1)、求证:CD是⊙O的切线.(2)、若tan∠BED= , AC=9,求⊙O的半径.23. 如图,已知抛物线()与x轴交于点和点B , 与y轴交于点C , 对称轴为 .
(1)、求证:CD是⊙O的切线.(2)、若tan∠BED= , AC=9,求⊙O的半径.23. 如图,已知抛物线()与x轴交于点和点B , 与y轴交于点C , 对称轴为 . (1)、求抛物线的解析式;(2)、如图1,若点P是线段上的一个动点(不与点B , C重合),过点P作y轴的平行线交抛物线于点Q , 连接 . 当线段长度最大时,判断四边形的形状并说明理由;(3)、如图2,在(2)的条件下,D是的中点,过点Q的直线与抛物线交于点E , 且 . 在y轴上是否存在点F , 使得为等腰三角形?若存在,求点F的坐标;若不存在,请说明理由.24. 综合与实践
(1)、求抛物线的解析式;(2)、如图1,若点P是线段上的一个动点(不与点B , C重合),过点P作y轴的平行线交抛物线于点Q , 连接 . 当线段长度最大时,判断四边形的形状并说明理由;(3)、如图2,在(2)的条件下,D是的中点,过点Q的直线与抛物线交于点E , 且 . 在y轴上是否存在点F , 使得为等腰三角形?若存在,求点F的坐标;若不存在,请说明理由.24. 综合与实践问题情境:图形的旋转是图形上的每一点在平面上绕着某个固定点旋转固定角度的位置移动.数学实践体验课上,张老师利用几何画板将两个大小不同的正方形进行旋转变换,并提出以下问题:如图①,四边形和四边形均为正方形,且点G在上,连接 , , 则与怎样的数量关系和位置关系.
 (1)、猜想定论:
(1)、猜想定论:猜想题目中的问题:与的数量关系是 , 位置关系是;
(2)、探索验证:如图②,将正方形以点A为旋转中心,按顺时针方向旋转一定角度,使得过点B(即点B在上),此时(1)中的结论是否成立,请说明理由;
(3)、拓展深入:如图③,在图②的基础上,过点A作于点H , 若 , , 请直接写出线段的长度.