黑龙江省大庆市肇源县东部五校联考2023-2024学年八年级下学期开学考试数学试题
试卷更新日期:2024-04-28 类型:开学考试
一、选择题(本大题共10小题,共30分。)
-
1. 若 , 则下列变形正确的是( )A、 B、 C、 D、2. 下列各式从左到右的变形中,是因式分解的为( ).A、 B、 C、 D、3. 下列说法正确的是( )A、平行四边形是轴对称图形 B、平行四边形的邻边相等 C、平行四边形的对角线互相垂直 D、平行四边形的对角线互相平分4. 如果9x2+kx+25是一个完全平方式,那么k的值是( )A、±30 B、30 C、15 D、±55. 下列图形中,既是轴对称图形,又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 6. 如图,已知函数y1=3x和y2=kx+b的图象相交于点A(1,3),则关于x的不等式kx+b<3x的解集为( )
6. 如图,已知函数y1=3x和y2=kx+b的图象相交于点A(1,3),则关于x的不等式kx+b<3x的解集为( ) A、x<3 B、x>3 C、x<1 D、x>17. 如图,△ABC中,AB=AC,点D在AC边上,且BD=BC=AD,则∠A的度数为( )
A、x<3 B、x>3 C、x<1 D、x>17. 如图,△ABC中,AB=AC,点D在AC边上,且BD=BC=AD,则∠A的度数为( ) A、30° B、36° C、45° D、70°8. 如图,在□ABCD中,AB=3,BC=5,AC的垂直平分线交AD于点E,则△CDE的周长是( )
A、30° B、36° C、45° D、70°8. 如图,在□ABCD中,AB=3,BC=5,AC的垂直平分线交AD于点E,则△CDE的周长是( ) A、6 B、8 C、9 D、109. 某口琴社团为练习口琴,第一次用1200元买了若干把口琴,第二次在同一家商店用2200元买同一款的口琴,这次商家每把口琴优惠5元,结果比第一次多买了20把.求第一次每把口琴的售价为多少元?若设第一次买的口琴为每把x元,列方程正确的是( )A、 B、 C、 D、10. 已知a、b、c是△ABC的三边长,且满足 , 则△ABC的形状是 ( )A、直角三角形 B、等腰三角形 C、等边三角形 D、不能确定
A、6 B、8 C、9 D、109. 某口琴社团为练习口琴,第一次用1200元买了若干把口琴,第二次在同一家商店用2200元买同一款的口琴,这次商家每把口琴优惠5元,结果比第一次多买了20把.求第一次每把口琴的售价为多少元?若设第一次买的口琴为每把x元,列方程正确的是( )A、 B、 C、 D、10. 已知a、b、c是△ABC的三边长,且满足 , 则△ABC的形状是 ( )A、直角三角形 B、等腰三角形 C、等边三角形 D、不能确定二、填空题(本大题共8小题,共24分)
-
11. 如果一个三角形是轴对称图形,且有一个角是60度,那么这个三角形的形状是。12. 已知△ABC中,∠A = , 角平分线BE、CF交于点O,则∠BOC = °13. 若分式 的值为零,则 =。14. 三条公路两两相交,要在该平面内修建一个加油站,使加油站到三条公路的距离都相等,则满足条件的加油站可以建 处。15. 若一个多边形的内角和是外角和的3倍,则这个多边形是边形.16. 要使代数式有意义,则的取值范围是 。17. 如图,在Rt△ABC 中,∠ACB=90°,∠A=32°,将△ABC绕点C按顺时针方向旋转后得到△EDC,此时点D在AB边上,则旋转角的大小为度。
 18. 如图,平行四边形ABCD的对角线AC,BD相交于点O,点E,F分别是线段AO,BO的中点.若AC+BD=24cm,△OAB的周长是18cm,则EF的长为 cm.
18. 如图,平行四边形ABCD的对角线AC,BD相交于点O,点E,F分别是线段AO,BO的中点.若AC+BD=24cm,△OAB的周长是18cm,则EF的长为 cm.
三、解答题(本大题共10小题,共66分)
-
19. 因式分解:(1)、﹣3x3+6x2y﹣3xy2;(2)、(x+y)(x﹣y)﹣(y﹣x)2 .20. 解不等式组:21. 解分式方程:(1)、(2)、22. 先化简,再求值: 其中x=2。23. 如图,正方形网格中,每个小正方形的边长都是一个单位长度,在平面直角坐标系中,△ABC的三个顶点A(5,5),B(6,3),C(2,1)均在格点上.在平面直角坐标系中,△ABC的位置如图所示.(每个小方格都是边长1个单位长度的正方形)
 (1)、画出将△ABC向左平移8个单位长度得到的△A1B1C1 , 并写出点A1的坐标;(2)、画出△ABC绕点C顺时针旋转90°后得到的△A2B2C2 , 并写出点A2的坐标.24. 如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB,如果DE=5cm,∠CAD=32°,求CD的长度及∠B的度数.
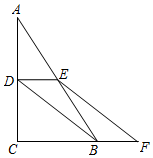
(1)、画出将△ABC向左平移8个单位长度得到的△A1B1C1 , 并写出点A1的坐标;(2)、画出△ABC绕点C顺时针旋转90°后得到的△A2B2C2 , 并写出点A2的坐标.24. 如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB,如果DE=5cm,∠CAD=32°,求CD的长度及∠B的度数. 25. 如图,已知在□ABCD中,点E、F分别是边AD、CD的中点,过点E、F的直线交BA、BC的延长线于点G、H,连接AC.
25. 如图,已知在□ABCD中,点E、F分别是边AD、CD的中点,过点E、F的直线交BA、BC的延长线于点G、H,连接AC.求证:四边形ACHE是平行四边形;
 26. 2022年冬奥会吉祥物冰墩墩一夜之间火遍全球,各种冰墩墩的玩偶,挂件,灯饰等应运而生.某学校决定购买A,B两种型号的冰墩墩饰品作为纪念品,已知A种比B种每件多25元,预算资金为1700元:其中800元购买A种商品,其余资金购买B种商品,且购买B种的数量是A种的3倍.(1)、求A,B两种饰品的单价.(2)、购买当日,正逢开学季搞促销,所有商品均按原价八折销售,学校调整了购买方案:不超过预算资金且购买A种饰品的资金不少于720元,A,B两种饰品共100件:问购买A,B两种饰品有哪几种方案?
26. 2022年冬奥会吉祥物冰墩墩一夜之间火遍全球,各种冰墩墩的玩偶,挂件,灯饰等应运而生.某学校决定购买A,B两种型号的冰墩墩饰品作为纪念品,已知A种比B种每件多25元,预算资金为1700元:其中800元购买A种商品,其余资金购买B种商品,且购买B种的数量是A种的3倍.(1)、求A,B两种饰品的单价.(2)、购买当日,正逢开学季搞促销,所有商品均按原价八折销售,学校调整了购买方案:不超过预算资金且购买A种饰品的资金不少于720元,A,B两种饰品共100件:问购买A,B两种饰品有哪几种方案?