浙江省杭州市西湖区公益中学2023-2024学年九年级下学期3月月考数学试卷

试卷更新日期：2024-04-28 类型：月考试卷

进入出卷网下载

一、选择题。本大题有10个小题，每小题3分，共30分。在每小题给出的四个选项中，只有一项是符合题目要求的.

1. $- \frac{1}{10}$ 的绝对值是（）

A、 $- \frac{1}{10}$ B、-10 C、 $\frac{1}{10}$ D、10

查看试题解析
2. 下列运算正碍的是（）

A、 $2 a^{2} - a^{2} = 2$ B、 ${(a b^{2})}^{2} = a b^{4}$ C、 $a^{2} \cdot a^{3} = a^{6}$ D、 $a^{8} \div a^{4} = a^{4}$

查看试题解析
3. 今冬，哈尔游旅游火了! “因为 “尔浣” 的真情实意款待，在 2024 年元旦小长假的旅游收入 59.14 亿元，将数据 “ 59.14 亿" 用科学记数法表示为（）

A、 $5.914 \times 1 0^{1}$ B、 $0.5914 \times 1 0^{10}$ C、 $5.914 \times 1 0^{10}$ D、 $5.914 \times 1 0^{9}$

查看试题解析
4. 围棋起源于中国，古代称之为 “㡣”，至今已有 4000 多年的历史. 一棋谱中四部分的截图由黑白棋子摆成的图案是中心对称的是（）

A、 B、 C、 D、

查看试题解析
5. 爬坡时坡面与水平面夹角为 $α$ ，则每爬 $1 m$ 耗能 $(1.025 - c o s α) J$ ，若某人爬了 $1000 m$ ，该坡角为 $30 °$ ，则他耗能 $($ 　　 $)$ （参考数据： $\sqrt{3} \approx 1.732$ ， $\sqrt{2} \approx 1.414)$

A、 $58 J$ B、 $159 J$ C、 $1025 J$ D、 $1732 J$

查看试题解析
6. 如图， $⊙ O$ 半径长 $2 c m$ ，点 $A$ 、 $B$ 、 $C$ 是 $⊙ O$ 三等分点，点 $D$ 为圆上一点，连接 $A D$ ，且 $A D = 2 \sqrt{2} c m$ ， $C D$ 交 $A B$ 于点 $E$ ，则 $∠ B E D = ($ $)$

A、 $75 °$ B、 $65 °$ C、 $60 °$ D、 $55 °$

查看试题解析
7. 如图，在矩形 $A B C D$ 中，对角线 $A C$ 与 $B D$ 相交于点 $O$ ， $∠ A B D = 60 °$ ， $A E ⊥ B D$ ，垂足为点 $E$ ， $F$ 是 $O C$ 的中点，连接 $E F$ ，若 $E F = 2 \sqrt{3}$ ，则矩形 $A B C D$ 的周长是（）

A、 $16 \sqrt{3}$ B、 $8 \sqrt{3} + 4$ C、 $4 \sqrt{3} + 8$ D、 $8 \sqrt{3} + 8$

查看试题解析
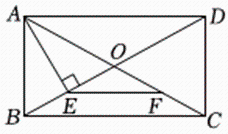8. 不透明的盒子放有三张大小、形状及质地相同的卡片，卡片上分别马有李白《峨眉山月歌》，李白《渡荆门送别》和王维《寄荆州张丞相》三首诗，小明从禽子中随机抽取两张卡片，卡片上诗的作者都是李白的概率是（）

A、 $\frac{1}{3}$ B、 $\frac{1}{4}$ C、 $\frac{1}{5}$ D、 $\frac{1}{6}$

查看试题解析
9. 关于x的二次函数y=mx²-（2m-1）x-2（m≠0），甲同学认为：若m＜0，则当x≤1时，y随x的增大而增大．乙同学认为：若该二次函数的图象在x轴上截得的线段长为3，则m的值是1或 $- \frac{1}{5}$ ，以下对两位同学的看法判断正确的是（　　）

A、甲、乙都错误 B、甲、乙都正确 C、甲正确、乙错误 D、甲错误、乙正确

查看试题解析
10. 如图，在正方形 A B C D 中，点 E， F 分别在 A D， B C 上，且保持 $A E = C F$ ，在 C D 上取一点 $G$ ，连结 G F，使 E F 恰好平分 $∠ B F G$ ，连结 E G. 若要求正方形ABCD的面积，则只需要知道（）

A、△EFG的面积 B、△EDG的面积 C、△CFG的周长 D、AEDG的周长

查看试题解析

二、填空题：本大题有6个小题，每小题4分。共24分.

11. 若代数式 $\sqrt{x + 1}$ 在实数范围内有意义，则实数x的取值范围是

查看试题解析
12. 分解因式： $2 x^{2} - 8$ = ．

查看试题解析
13. 如图所示，在菱形ABCD中，tanB=0.75，AE⊥BC，垂足为E，若CE=2，则菱形周长为

查看试题解析
14. 底面半径为 $10 c m$ ，高为 $10 \sqrt{3} c m$ 的圆雉的侧面展开图的面积为 $c m^{2}$ ，

查看试题解析
15. 已知 $a$ 、 $b$ 、 $c$ 均为实数，且 $a + b = 4$ ， $2 c^{2} - a b = 4 \sqrt{3} c - 10$ ，则 $a b c =$ ．

查看试题解析
16. 如图， $⊙ O$ 是 $△ A B C$ 的外接图， A B 是 $⊙ O$ 的直径， $∠ A C B$ 的平分线交 $⊙ O$ 于点 $D$ ，过点 $A$ 作 $A E ⊥ C D$ ，垂足为点 $E$ .① $A C = 1, B C = 2$ ，则 $A D =$ ②若∠DBE=2∠ABC，则 $\frac{D E}{C E} =$

查看试题解析

三、解答题。本大题有7个小题，共66分。解答应写出文字说明、证明过程或演算步骤.

17. 如图，在4×4的方格纸中，点A、B在格点上．请使用无刻度的直尺技要求画出格点线段（线段的端点在格点上），并写出结论.

(1)、在图1中画一条线段垂直AB.

(2)、在图2中画一条线段平分AB.

查看试题解析
18. 已知线段 $A B = 2$ ，点 $P$ 是线段 A B 的黄金分割点 $(A P > B P)$

(1)、求线段 A P的长

(2)、以A B 为三角形的一边作 $△ A B Q$ ，使得 $B Q = A P$ ，连接 Q P，若 Q P 平分 $∠ A Q B$ ，求 A Q 的长.

查看试题解析
19. 在一个不透明的盒子里装着除颜色外完全相同的黑、白两种小球共40个，小明做摸球试验，他将盒子里面的球搅匀后从中随机摸出一个球记下颜色，再把它放回盒子中，不断重复上述过程，如表是试验中的一组统计数据：
摸球的次数n
100
200
300
500
800
1000
3000
摸到白球的次数m
70
128
171
302
481
599
1806
摸到白球的频率 $\frac{m}{n}$
0.7
0.64
0.57
0.604
0.601
0.599
0.602

(1)、请估计当n很大时，摸到白球的概率为（精确到0.1） .

(2)、估算盒子里有白球多少个？

(3)、若向盒子里再放入x个除颜色以外其他完全相同的球，这x个球中白球只有1个。每次将球搅拌均匀后，任意摸出一个球记下颜色再放回，通过大量里复摸球试验后发现，摸到白球的频率稳定在0.5，那么可以推测出x最有可能是多少？

查看试题解析
20. 在等边三角形ABC中，点E在B边上，点D在 CB的延长线上，且DE=EC.

(1)、如图1，当E为AB中点时，求证。CB=2BD：

(2)、如图2，若AB=12，AE=2，求CD的长.

查看试题解析
21. 如图所示，双曲线 $y = \frac{k}{x} (k \neq 0)$ 的图象与一次函数 $y = - \frac{1}{2} x - 1$ 的图象交于 $A (m, 1), B (2, n)$ 两点.

(1)、求反比例函数的解析式：

(2)、设直线 A B 与 $x$ 轴交于点 $C$ ，若 $P$ 为 $y$ 轴正半轴上一点，当 $△ A P C$ 的面积为3时，求点P的坐标.

查看试题解析
22. 在平面直角坐标系 x O y 中，点 $A (- 1, m)$ ，点 $B (3, n)$ 在挞物线 $y = a x^{2} + b x + c (a > 0)$ 上. 设拋物线的对称轴为直线 $x = t$ .

(1)、当 $t = 2$ 时，
①直接马出 $b$ 与 $a$ 满足的等量关系
②比较m。n的大小，并说明理由；

(2)、已知点 $C (x_{0}, p)$ 在该抛物线上，若对于 $3 < x_{0} < 4$ ，都有 $m > p > n$ ，求 $t$ 的取值范围.

查看试题解析
23. 如图

(1)、问题提出
如图①，在 $Δ A B C$ 中，AB=AC=10，BC=12，点O是 $Δ A B C$ 的外接圆的圆心。求OB 的长，

(2)、问题探究
如图②，已知矩形ABCD，AB=4，AD=6，点E为AD的中.，以BC为直径作半圆O，点Р为半圆O上一动点，求E、P之间的最大距离

(3)、问题解决
某地有一块如图③所示的果园，果园是由四边形BCD和弦CB与其所对的劣场地组成的，果园主人现要从入口D到 $\overset{⌢}{B C}$ 的一点Р修建一条笔直的小路 DP、已知AD∥BC，∠ADB=45 °. BD= 120 $\sqrt{2}$ 米，BC=160米，过弦BC的中点E作 EF⊥BC交 $\overset{⌢}{B C}$ 于点F，又测得EF=40米．修建小路平均每米需要40元（小路宽度不计），不考虑其他因素，请你根据以上信息，帮助果园主人计算修建这条小路最多要花费多少元？

查看试题解析
24. 如图，在 $△ A B D$ 中， $A B = A D, ∠ B A D = α$ . 点 $C$ 昆 B D 延长线上一动点，连接 A C，将 A C 绕点 $A$ 轸时针旋转 $α$ 得到 A E，连接 D E 交 A C 于点 $F$ .

(1)、求证： $∠ C = ∠ E$ ；

(2)、如图1，若DE⊥AB，DF=2，FE=7，求BD的大小；

(3)、如图 2，若点F为 A C 中点， $\frac{S_{Δ A D F}}{S_{Δ A B C}} = \frac{1}{n + 2}$ ， CD=4，求 A B 的长（用含n的代数式表示

查看试题解析

摸球的次数n	100	200	300	500	800	1000	3000
摸到白球的次数m	70	128	171	302	481	599	1806
摸到白球的频率 $\frac{m}{n}$	0.7	0.64	0.57	0.604	0.601	0.599	0.602