【北师大版·数学】2024年中考二轮复习之图形认识初步
试卷更新日期:2024-04-28 类型:二轮复习
一、选择题
-
1. 下列图形是正方体展开图的个数为( )
 A、1个 B、2个 C、3个 D、4个2. 如图是一个正方体的展开图,把展开图折叠成小正方体后,和“建”字所在面相对的面上的字是( )
A、1个 B、2个 C、3个 D、4个2. 如图是一个正方体的展开图,把展开图折叠成小正方体后,和“建”字所在面相对的面上的字是( ) A、跟 B、百 C、走 D、年3. 下列哪个图形是正方体的展开图( )A、
A、跟 B、百 C、走 D、年3. 下列哪个图形是正方体的展开图( )A、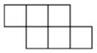 B、
B、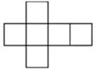 C、
C、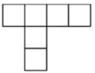 D、
D、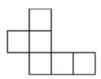 4. 下面图形经过折叠可以围成一个棱柱的是( )A、
4. 下面图形经过折叠可以围成一个棱柱的是( )A、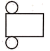 B、
B、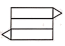 C、
C、 D、
D、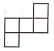 5. 如图是某几何体的展开图,该几何体是( )
5. 如图是某几何体的展开图,该几何体是( ) A、长方体 B、圆柱 C、圆锥 D、三棱柱6. 如图,是由个相同的小正方体组成的几何体,其左视图是( )
A、长方体 B、圆柱 C、圆锥 D、三棱柱6. 如图,是由个相同的小正方体组成的几何体,其左视图是( )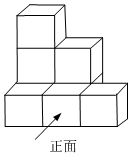 A、
A、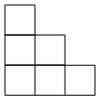 B、
B、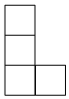 C、
C、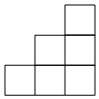 D、
D、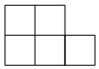 7. 下列图形中,主视图和左视图一样的是( )A、
7. 下列图形中,主视图和左视图一样的是( )A、 B、
B、 C、
C、 D、
D、 8. 把图中三棱柱沿表面展开,所得到的平面图形可以是( )
8. 把图中三棱柱沿表面展开,所得到的平面图形可以是( ) A、
A、 B、
B、 C、
C、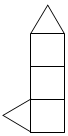 D、
D、 9. 下列四个几何体中,左视图为圆的是( )A、
9. 下列四个几何体中,左视图为圆的是( )A、 B、
B、 C、
C、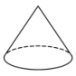 D、
D、 10. 如图是正方体的一种不完整的表面展开图.下面是四位同学补画的情况(图中的阴影部分),其中补画正确的是( )
10. 如图是正方体的一种不完整的表面展开图.下面是四位同学补画的情况(图中的阴影部分),其中补画正确的是( ) A、
A、 B、
B、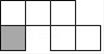 C、
C、 D、
D、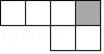
二、填空题
-
11. 如图,是一个正方体的展开图,那么写有“青”字面的对面上的字是 .
 12. 如图,是由10个完全相同的小正方体堆成的几何体.若现在你还有若干个相同的小正方体,在保证该几何体的从上面、从正面、从左面看到的图形都不变的情况下,最多还能放个小正方体.
12. 如图,是由10个完全相同的小正方体堆成的几何体.若现在你还有若干个相同的小正方体,在保证该几何体的从上面、从正面、从左面看到的图形都不变的情况下,最多还能放个小正方体. 13. 如图是一个几何体的三视图(图中尺寸单位:cm),根据图中所示数据计算这个几何体的表面积为 cm2 .
13. 如图是一个几何体的三视图(图中尺寸单位:cm),根据图中所示数据计算这个几何体的表面积为 cm2 . 14. 一个上下底密封的纸盒的三视图如图所示,请你根据图中的数据,计算这个密封纸盒的表面积为m2 . (结果保留π)
14. 一个上下底密封的纸盒的三视图如图所示,请你根据图中的数据,计算这个密封纸盒的表面积为m2 . (结果保留π) 15. 任意放置以下几何体:正方体、圆柱、圆锥,则三视图都完全相同的几何体是 .
15. 任意放置以下几何体:正方体、圆柱、圆锥,则三视图都完全相同的几何体是 .三、综合题
-
16. 数学学习小组的同学共同探究体积为330mL圆柱形有盖容器(如图所示)的设计方案.,他们想探究容器表面积与底面半径的关系.

具体研究过程如下,请补充完整:
⑴建立模型:设该容器的表面积为S , 底面半径为cm,高为cm,则
, ①
, ②
由①式得 , 代入②式得
. ③
可知,S是x的函数,自变量x的取值范围是 .
⑵探究函数:
根据函数解析式③,按照下表中自变量x的值计算(精确到个位),得到了S与x的几组对应值:
…
1
1.5
2
2.5
3
3.5
4
4.5
5
5.5
6
…
…
666
454
355
303
277
266
266
274
289
310
336
…
在下面平面直角坐标系中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;

⑶解决问题:根据图表回答,
①半径为2.4cm的圆柱形容器比半径为4.4cm的圆柱形容器表面积 . (填“大”或“小”);
②若容器的表面积为300 , 容器底面半径约为cm(精确到0.1).
17. 某工厂要加工一批上下底密封纸盒,设计者给出了密封纸盒的三视图,如图1. (1)、由三视图可知,密封纸盒的形状是;(2)、根据该几何体的三视图,在图2中补全它的表面展开图;(3)、请你根据图1中数据,计算这个密封纸盒的表面积.(结果保留根号)18. 一张宽为6cm的平行四边形纸带ABCD如图1所示,AB=10cm,小明用这张纸带将底面周长为10cm直三棱柱纸盒的侧面进行包贴(要求包贴时没有重叠部分).小明通过操作后发现此类包贴问题可将直三棱柱的侧面展开进行分析.
(1)、由三视图可知,密封纸盒的形状是;(2)、根据该几何体的三视图,在图2中补全它的表面展开图;(3)、请你根据图1中数据,计算这个密封纸盒的表面积.(结果保留根号)18. 一张宽为6cm的平行四边形纸带ABCD如图1所示,AB=10cm,小明用这张纸带将底面周长为10cm直三棱柱纸盒的侧面进行包贴(要求包贴时没有重叠部分).小明通过操作后发现此类包贴问题可将直三棱柱的侧面展开进行分析.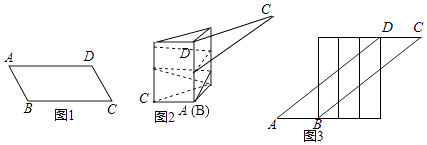 (1)、若纸带在侧面缠绕三圈,正好将这个直三棱柱纸盒的侧面全部包贴满.则纸带AD的长度为 cm;(2)、若AD=100cm,纸带在侧面缠绕多圈,正好将这个直三棱柱纸盒的侧面全部包贴满.则这个直三棱柱纸盒的高度是 cm.
(1)、若纸带在侧面缠绕三圈,正好将这个直三棱柱纸盒的侧面全部包贴满.则纸带AD的长度为 cm;(2)、若AD=100cm,纸带在侧面缠绕多圈,正好将这个直三棱柱纸盒的侧面全部包贴满.则这个直三棱柱纸盒的高度是 cm.四、作图题
-
19. 画一个正方体的三种平面展开图,要求展开图是中心对称图形.

五、解答题
-
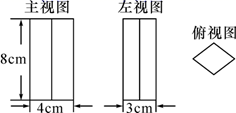
20. 一个几何体的三视图如图所示,它的俯视图为菱形.请写出该几何体的形状,并根据图中所给的数据求出它的侧面积.
 21. 如图是一个正方体的展开图,标注了字母A的面是正方体的正面,如果正方体的左面与右面所标注代数式的值相等,求x的值.
21. 如图是一个正方体的展开图,标注了字母A的面是正方体的正面,如果正方体的左面与右面所标注代数式的值相等,求x的值.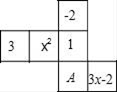
六、实践探究题
-
22. 阅读下面材料:
实际问题:如图(1),一圆柱的底面半径为5厘米,BC是底面直径,高AB为5厘米,求一只蚂蚁从点A出发沿圆柱表面爬行到点C的最短路线,小明设计了两条路线.

解决方案:
路线1:侧面展开图中的线段AC,如图(2)所示,
设路线l的长度为l1:则l12=AC2=AB2+BC2=52+(5π)2=25+25π2;
路线2:高线AB+底面直径BC,如图(1)所示.
设路线2的长度为l2:则l22=(AB+BC)2=(5+10)2=225.
为比较l1 , l2的大小,我们采用“作差法”:
∵l12﹣l22=25(π2﹣8)>0∴l12>l22∴l1>l2 ,
小明认为应选择路线2较短.
(1)、问题类比:小亮对上述结论有些疑惑,于是他把条件改成:“圆柱的底面半径为1厘米,高AB为5厘米.”.请你用上述方法帮小亮比较出l1与l2的大小:
(2)、问题拓展:请你帮他们继续研究:在一般情况下,当圆柱的底面半径为r厘米时,高为h厘米,蚂蚁从A点出发沿圆柱表面爬行到点C,当 满足什么条件时,选择路线2最短?请说明理由.
(3)、问题解决:如图(3)为2个相同的圆柱紧密排列在一起,高为5厘米,当蚂蚁从点A出发沿圆柱表面爬行到C点的两条路线长度相等时,求圆柱的底面半径r.(注:按上面小明所设计的两条路线方式).
-