【北师大版·数学】2024年中考二轮复习之基本平面图形
试卷更新日期：2024-04-28 类型：二轮复习
一、选择题
-
1. 某同学从A地出发沿北偏东30°的方向步行5分钟到达B地，再由B地沿南偏西40°的方向步行到达C地，则∠ABC的大小为（ ）A、10° B、20° C、35° D、70°2. 数轴上表示﹣6和4的点分别是A和B ， 则线段AB的长度是（ ）A、﹣2 B、2 C、﹣10 D、103. 若一个多边形从同一个顶点出发可以作5条对角线，则这个多边形的边数为（ ）A、6 B、7 C、8 D、94. 从多边形一个顶点出发向其余的顶点引对角线，将多边形分成6个三角形，则此多边形的边数为（ ）A、6 B、7 C、8 D、95. 已知数轴上的三点A、B、C，分别表示有理数a、1、﹣1，那么|a+1|表示为（ ）
A、A、B两点间的距离 B、A、C两点间的距离 C、A、B两点到原点的距离之和 D、A、C两点到原点的距离之和6. 如图所示，已知∠AOC=∠BOD=70°，∠BOC=30°，则∠AOD的度数为（ ）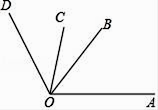
A、100° B、110° C、130° D、140°7.如图，为了监控一不规则多边形艺术走廊内的活动情况，现已在A，B两处各安装了一个监控探头（走廊内所用探头的观测区域为圆心角最大可取到180°的扇形），图中的阴影部分是A处监控探头观测到的区域.要使整个艺术走廊都能被监控到，还需再安装一个监控探头，则安装的位置是（ )
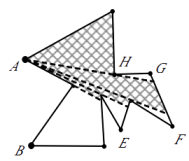A、E处 B、F处 C、G处 D、H处8. 从一个n边形的同一个顶点出发，分别连接这个顶点与其余各顶点，若把这个多边形分割成6个三角形，则n的值是（ ）A、6 B、7 C、8 D、99. 下列关系式正确的是（ ）A、35.5°=35°5′ B、35.5°=35°50′ C、35.5°＜35°5′ D、35.5°＞35°5′10. 下列性质中，菱形具有但矩形不一定具有的是（ ）A、对边相等 B、对边平行 C、对角相等 D、对角线互相垂直二、填空题
-
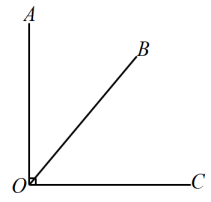
11. 如图， ， 则的度数为 ．
12. 在平面直角坐标系中，点（3，﹣2）到原点的距离是 ．13. 计算：18°30′＝°．14. 如图所示，圆柱的高AB＝3，底面直径BC＝3，现在有一只蚂蚁想要从A处沿圆柱表面爬到对角C处捕食，则它爬行的最短距离是 ．
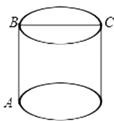15. 点C在射线AB上，若AB=3，BC=2，则AC为三、作图题
-
16. 作图题：如图，已知点A，点B，直线l及l上一点M.
(1)、连接MA，并在直线l上作出一点N，使得点N在点M的左边，且满足MN＝MA；(2)、请在直线l上确定一点O，使点O到点A与点O到点B的距离之和最短，并写出画图的依据.四、解答题
-
17.
如图，点C在线段AB上，AC=8 cm，CB=6 cm，点M、N分别是AC、BC的中点．
（1）求线段MN的长；
（2）若C为线段AB上任一点，满足AC+CB=a cm，其它条件不变，你能猜想MN的长度吗？并说明理由；
（3）若C在线段AB的延长线上，且满足AC﹣BC=bcm，M、N分别为AC、BC的中点，你能猜想MN的长度吗？请画出图形，写出你的结论，并说明理由；
（4）你能用一句简洁的话，描述你发现的结论吗？
五、综合题
-
18. 为了维护国家主权和海洋权利，海监部门对我国领海实现了常态化巡航管理，如图，正在执行巡航任务的海监船以每小时50海里的速度向正东方航行，在A处测得灯塔P在北偏东60°方向上，继续航行1小时到达B处，此时测得灯塔P在北偏东30°方向上．
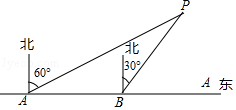(1)、求∠APB的度数；(2)、已知在灯塔P的周围25海里内有暗礁，问海监船继续向正东方向航行是否安全？
-
-