【北师大版·数学】2024年中考二轮复习之概率

试卷更新日期：2024-04-28 类型：二轮复习

进入出卷网下载

一、选择题

1. 盒子里有10个球，它们只有颜色不同，其中红球有7个，黄球有2个，黑球有1个．幸幸从中任意摸一个球，下面说法正确的是（）

A、一定是红球 B、摸出红球的可能性最大 C、不可能是黑球 D、摸出黄球的可能性最小

查看试题解析
2. 抛掷一枚质地均匀的正方体骰子，骰子各面分别标有数字1、2、3、4、5、6，则出现朝上的数字小于3的概率是（）

A、 $\frac{1}{6}$ B、 $\frac{1}{3}$ C、 $\frac{1}{2}$ D、 $\frac{2}{3}$

查看试题解析
3. 吴老师在演示概率试验时，连续随机抛掷一枚质地均匀的骰子，前3次的结果是“6”，则第4次的结果是“6”的概率是（）

A、0 B、 $\frac{1}{6}$ C、 $\frac{1}{2}$ D、1

查看试题解析
4. 下列说法正确的是（）

A、“守株待兔”是必然事件 B、“概率为0.0001的事件”是不可能事件 C、“在一个只装有5个红球的袋中随机摸出1个球是红球”是必然事件 D、任意掷一枚质地均匀的硬币20次，正面向上的次数一定是10次

查看试题解析
5. 下列事件中，是必然事件的是（）

A、明天北京新冠肺炎新增0人 B、车辆随机到达一个路口，遇到红灯 C、如果a²＝b² ，那么a＝b D、将花生油滴在水中，油会浮在水面上

查看试题解析
6. 数学老师将全班分成7个小组开展小组合作学习，采用随机抽签确定一个小组进行展示活动，则第3个小组被抽到的概率是（）

A、 $\frac{1}{7}$ B、 $\frac{1}{3}$ C、 $\frac{1}{21}$ D、 $\frac{1}{10}$

查看试题解析
7. 已知一口袋中放有红、白、黑三种颜色的球共50个，它们除颜色外其他都一样，一位同学通过多次试验后发现摸到红、白色的频率基本稳定是45%和15%，则袋中黑球的个数可能是（　　）

A、16 B、18 C、20 D、22

查看试题解析
8. 在学习了“用频率估计概率”这一节内容后，某课外兴趣小组利用计算器进行模拟试验来探究“6个人中有2个人同月过生日的概率”，他们将试验中获得的数据记录如下：
试验次数
100
300
500
1000
1600
2000
“有2个人同月过生日”的次数
80
229
392
779
1251
1562
“有2个人同月过生日”的频率
0.8
0.763
0.784
0.779
0.782
0.781
通过试验，该小组估计“6个人中有2个人同月过生日”的概率（精确到0.01）大约是（　　）

A、0.8 B、0.784 C、0.78 D、0.76

查看试题解析
9. 下列事件中是必然事件的是（）

A、打开电视机，正在播放《开学第一课》 B、经过有交通信号灯的路口，遇到红灯 C、任意画一个三角形，其内角和是 $180 °$ D、买一张彩票，一定不会中奖

查看试题解析
10. “天宫课堂”第二课3月23日在中国空间站开讲，包括六个项目：太空“冰雪”实验、液桥演示实验、水油分离实验、太空抛物实验、空间科学设施介绍与展示、天地互动环节．若随机选取一个项目写观后感，则恰好选到“实验”项目的概率是（）

A、 $\frac{1}{3}$ B、 $\frac{1}{2}$ C、 $\frac{2}{3}$ D、 $\frac{5}{6}$

查看试题解析

二、填空题

11. 足球、篮球、排球，“三大球”单列成为体育中考必考项目之一，考生需任选一项参加考试，甲生选择考排球的概率为．

查看试题解析
12. 习近平总书记在党的二十大报告中强调：“青年强，则国家强”．小明同学将“青”“年”“强”“则”“国”“家”“强”这7个字，分别书写在大小、形状完全相同的7张卡片上，搅匀后从中随机抽取一张，则这张卡片上恰好写着“强”字的概率是

查看试题解析
13. 有五张正面分别标有数字-2，-1，0，1，2的不透明卡片，它们除数字不同外其余全部相同．现将它们背面朝上，洗匀后从中任取一张，将该卡片上的数字记为a，将该卡片放回洗匀后从中再任取一张，将该卡片上的数字记为b，则 $a b$ 为非负数的概率为．

查看试题解析
14. 在一个不透明的口袋中装有若干个小球（除颜色不同，其余都相同），其中有3个红球且从中随机摸出一个球是红球的概率为 $\frac{1}{5}$ ，那么口袋中共有小球个。

查看试题解析
15. 一个不透明的袋子中装有若干个红球和6个黄球，它们除颜色外都相同，从中随机摸出一个球，记下颜色后放回，通过大量反复实验发现，摸到黄球的频率约为0.3，由此推测这个袋中红球的个数为.

查看试题解析

三、解答题

16. 小红和小明做游戏：在一个不透明口袋中装有6个红球.9个黄球.3个绿球，这些球除颜色外没有任何区别．从中任意摸出一个球．摸到黄球小明胜，摸到的球不是黄球小红胜，这个游戏公平吗？请说明详细的理由．

查看试题解析
17. 某商场为了吸引顾客，设立了一个可以自由转动的转盘（转盘被等分成个扇形，如图）并规定：顾客在本商场每消费元，就能获得一次转动转盘的机会，如果转盘停止后，指针正好对准红、黄或绿色区域，顾客就可以分别获得 100 元、 50 元、 20 元的购物券．某顾客消费 210 元，他转动转盘获得购物券的概率是多少?他得到 100 元、 50 元、 20 元购物券的概率分别是多少?

查看试题解析
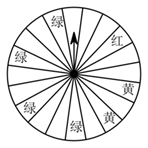18.
一粒木质中国象棋棋子“車”，它的正面雕刻一个“車”字，它的反面是平的，将棋子从一定高度下抛，落地反弹后可能是“車”字面朝上，也可能是“車”字朝下．由于棋子的两面不均匀，为了估计“車”字朝上的机会，某实验小组做了棋子下抛实验，并把实验数据整理如下：
实验次数
20
40
60
80
100
120
140
160
“車”字朝上的频数
14
18
38
47
52

78
88
相应的频率
0.7
0.45
0.63
0.59
0.52
0.55
0.56

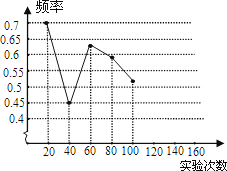
（1）请将表中数据补充完整，并画出折线统计图中剩余部分．
（2）如果实验继续进行下去，根据上表数据，这个实验的频率将接近于该事件发生的机会，请估计这个机会约是多少？
（3）在（2）的基础上，进一步估计：将该“車”字棋子，按照实验要求连续抛2次，则刚好使“車”字一次字面朝上，一次朝下的可能性为多少？

查看试题解析
19. 某批乒乓球的质量检验结果如下：
抽取的乒乓球数n
200
500
1000
1500
2000
优等品频数m
188
471
946
1426
1898
优等品频率 $\frac{π}{n}$
0.940
0.942
0.946
0.951
0.949
（1）画出这批乒乓球“优等品”频率的折线统计图；
（2）这批乒乓球“优等品”的概率的估计值是多少？
（3）从这批乒乓球中选择5个黄球、13个黑球、22个红球，它们除颜色外都相同，将它们放入一个不透明的袋中．
①求从袋中摸出一个球是黄球的概率；
②现从袋中取出若干个黑球，并放入相同数量的黄球，搅拌均匀后使从袋中摸出一个是黄球的概率不小于 $\frac{1}{3}$ ，问至少取出了多少个黑球？

查看试题解析

四、综合题

20. 概率与统计在我们日常生活中应用非常广泛，请直接填出下列事件中所要求的结果：

(1)、有5张背面相同的纸牌，其正面分别标上数字“5”、“7”、“8”、“2”、“0”，将这5张纸牌背面朝上洗匀后摸出一张牌是奇数的概率为

(2)、七巧板是我国古代劳动人民的发明之一，它是由五块等腰直角三角形、一块正方形和一块平行四边形共七块板组成的．如图是一个用七巧板拼成的正方形飞镖游戏板，某人向该游戏板投掷飞镖一次（假设飞镖落在游戏板上），则飞镖落在阴影部分的概率是

查看试题解析
21. 如图是小华设计的自由转动的转盘，上面写10个有理数．想想看，转得下列各数的概率是多少？

(1)、转得正数；

(2)、转得正整数；

(3)、转得绝对值小于6的数；

(4)、转得绝对值大于等于8的数．

查看试题解析
22. 在一个不透明的袋中装有3个红球，4个黄球和若干白球，它们除颜色外其他都相同，将球搅匀，从中任意摸出一个球．

(1)、若袋内有5个白球，从中任意摸出一个球，是红球的概率为，是黄球的概率为，是白球的概率为．

(2)、如果任意摸出一个球是黄球的概率是 $\frac{2}{5}$ ，求袋中内有几个白球？

查看试题解析
23. 某商场的一次促销活动规定：凡在本商场购物，可转动转盘一次，并根据所转结果的折扣付账.

(1)、分别求出打九折，打八折的概率；

(2)、求不打折的概率：

(3)、小华和小明分别购买了价值200元的商品，活动后他们一共付钱360元，请直接写出他们获得优惠可能的情况.

查看试题解析

试验次数	100	300	500	1000	1600	2000
“有2个人同月过生日”的次数	80	229	392	779	1251	1562
“有2个人同月过生日”的频率	0.8	0.763	0.784	0.779	0.782	0.781

实验次数	20	40	60	80	100	120	140	160
“車”字朝上的频数	14	18	38	47	52		78	88
相应的频率	0.7	0.45	0.63	0.59	0.52	0.55	0.56

抽取的乒乓球数n	200	500	1000	1500	2000
优等品频数m	188	471	946	1426	1898
优等品频率 $\frac{π}{n}$	0.940	0.942	0.946	0.951	0.949