湖北省武汉市江夏区第一初级中学2023-2024学年下学期九年级数学3月测试题
试卷更新日期:2024-04-28 类型:月考试卷
一、选择题(共10小题,每小题3分,共30分)
-
1. 4的相反数是A、4 B、﹣4 C、 D、2. 经过有交通信号灯的路口,遇到绿灯,这个事件是( )A、随机事件 B、确定性事件 C、不可能事件 D、必然事件3. 下面几对图形中,相似的是( )A、
 B、
B、 C、
C、 D、
D、 4. 如图,在△ABC中,∠C=90°,BC=a,AC=b,AB=c,则下列选项正确的是( )
4. 如图,在△ABC中,∠C=90°,BC=a,AC=b,AB=c,则下列选项正确的是( ) A、 B、 C、 D、5. 如图,在 中, , , , ,则 的长为( )
A、 B、 C、 D、5. 如图,在 中, , , , ,则 的长为( )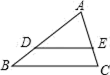 A、6 B、7 C、8 D、96. 关于反比例函数 , 下列结论正确的是( )A、图象位于第一、三象限 B、图象所在的每一个象限内,y随x的增大而增大 C、图象与y轴有公共点 D、图象经过点 , 则7. 如图,下列条件不能判定的是( )
A、6 B、7 C、8 D、96. 关于反比例函数 , 下列结论正确的是( )A、图象位于第一、三象限 B、图象所在的每一个象限内,y随x的增大而增大 C、图象与y轴有公共点 D、图象经过点 , 则7. 如图,下列条件不能判定的是( ) A、 , B、 C、 , D、 ,8. 已知 , 计算的值是( )A、1 B、 C、0.5 D、9. 如图, , 切于、两点,切于点 , 分别交 , 于 , , , 若的半径为r,的周长等于 , 则的值是( )
A、 , B、 C、 , D、 ,8. 已知 , 计算的值是( )A、1 B、 C、0.5 D、9. 如图, , 切于、两点,切于点 , 分别交 , 于 , , , 若的半径为r,的周长等于 , 则的值是( ) A、 B、 C、 D、10. 如图,在平面直角坐标系中,已知点 , , 若直线上总存在一点 , 使 , 则的取值范围为( )
A、 B、 C、 D、10. 如图,在平面直角坐标系中,已知点 , , 若直线上总存在一点 , 使 , 则的取值范围为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(共6小题,每小题3分,共18分)
-
11. 计算:tan45°=.12. 如图,一山坡的坡度为i=1: ,小辰从山脚A出发,沿山坡向上走了200米到达点B,则小辰上升了米.
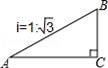 13. 如图,表示塔的高度,表示竹竿顶端到地面的高度,表示人跟到地面的高度, , 、在同一平面内,点 , , 在一条水平直线上,已知米,米,米,米,人从点远眺塔顶 , 视线恰好经过竹竿的顶端 . 根据以上信息,则塔的高度为米.
13. 如图,表示塔的高度,表示竹竿顶端到地面的高度,表示人跟到地面的高度, , 、在同一平面内,点 , , 在一条水平直线上,已知米,米,米,米,人从点远眺塔顶 , 视线恰好经过竹竿的顶端 . 根据以上信息,则塔的高度为米. 14. 如图,在中, , , 动点从点开始沿边运动,速度为 , 动点从点开始沿边运动,速度为如果、两动点同时运动,那么经过秒时与相似.
14. 如图,在中, , , 动点从点开始沿边运动,速度为 , 动点从点开始沿边运动,速度为如果、两动点同时运动,那么经过秒时与相似.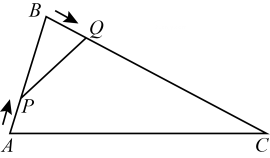 15. 如图,二次函数 , 其对称轴为直线 , 且与x轴交于点、 , 其中 , 下列结论:
15. 如图,二次函数 , 其对称轴为直线 , 且与x轴交于点、 , 其中 , 下列结论:①;②;③;④;⑤
其中正确的有 . (填写正确的序号)
 16. 如图,在中, , , 延长到D , 使得 , 点E在线段上运动(不与B , C重合)过E作平行四边形 , M为的中点,则的范围是 .
16. 如图,在中, , , 延长到D , 使得 , 点E在线段上运动(不与B , C重合)过E作平行四边形 , M为的中点,则的范围是 .
三、解答题(共8小题,共72分)
-
17. 计算: .18. 已知在直角中, , , , 求和大小.
 19. 如图,在△ABC中,AB=AC,点D、B、C、E在同一条直线上,且∠D=∠CAE.
19. 如图,在△ABC中,AB=AC,点D、B、C、E在同一条直线上,且∠D=∠CAE. (1)、求证:△ABD∽△ECA;(2)、若AC=8,CE=4,求BD的长度.20. 如图所示,以平行四边形的顶点为圆心,为半径作圆,分别交 , 于点 , , 延长交于点 .
(1)、求证:△ABD∽△ECA;(2)、若AC=8,CE=4,求BD的长度.20. 如图所示,以平行四边形的顶点为圆心,为半径作圆,分别交 , 于点 , , 延长交于点 . (1)、求证:;(2)、若 , , 求阴影部分弓形的面积.21. 如图是由小正方形组成的网格,每个小正方形的顶点叫做格点,的三个顶点都是格点.仅用无刻度的直尺在给定网格中完成画图,画图过程用虚线表示.
(1)、求证:;(2)、若 , , 求阴影部分弓形的面积.21. 如图是由小正方形组成的网格,每个小正方形的顶点叫做格点,的三个顶点都是格点.仅用无刻度的直尺在给定网格中完成画图,画图过程用虚线表示. (1)、在图(1)中,是格线上一点连接 , 直接写出 .(2)、在图(1)中,在线段上作出点 , 而且;(3)、在图(2)中,是边上一点, . 先将绕点顺时针旋转 , 得到线段 , 画出线段 , 再画点 , 使 , 两点关于直线对称.22. 冻雨是湖北不常见的天气情况,一旦遇上会对工作和生活带来不便甚至灾害.武汉市在二月份下了多次冻雨,许多树木因为冻雨结冰发生折断,我们对一无冰树枝置于武汉的2024年2月3日15点开始的冻雨下进行观察,发现一段含冰树枝的重量y(千克)和时间x(小时)近似满足二次函数关系: , 当时,该含冰树枝重9.75千克;当时,该含冰树枝增重到15.75千克.(1)、求二次函数的解析式.(2)、由经验可知当冻雨下含冰树枝的重量是未结冰时的3.5倍时,树枝会发生折断,请问树枝会折断吗?如果会,何时断裂,如果不会,说明理由.(3)、在(2)的树枝折发生折断的经验下,从2月3日15时,观察同一段树枝,经过10小时后,冻雨雨量开始增大,平均每小时的重量额外增加n千克,发现该段树枝在次日凌晨到之间折断,请直接写出n的范围 .23.
(1)、在图(1)中,是格线上一点连接 , 直接写出 .(2)、在图(1)中,在线段上作出点 , 而且;(3)、在图(2)中,是边上一点, . 先将绕点顺时针旋转 , 得到线段 , 画出线段 , 再画点 , 使 , 两点关于直线对称.22. 冻雨是湖北不常见的天气情况,一旦遇上会对工作和生活带来不便甚至灾害.武汉市在二月份下了多次冻雨,许多树木因为冻雨结冰发生折断,我们对一无冰树枝置于武汉的2024年2月3日15点开始的冻雨下进行观察,发现一段含冰树枝的重量y(千克)和时间x(小时)近似满足二次函数关系: , 当时,该含冰树枝重9.75千克;当时,该含冰树枝增重到15.75千克.(1)、求二次函数的解析式.(2)、由经验可知当冻雨下含冰树枝的重量是未结冰时的3.5倍时,树枝会发生折断,请问树枝会折断吗?如果会,何时断裂,如果不会,说明理由.(3)、在(2)的树枝折发生折断的经验下,从2月3日15时,观察同一段树枝,经过10小时后,冻雨雨量开始增大,平均每小时的重量额外增加n千克,发现该段树枝在次日凌晨到之间折断,请直接写出n的范围 .23. (1)、【基础巩固】如图,在中, , 是边上一点,是边上一点, . 求证: .(2)、【尝试应用】如图 , 在四边形中,点是边的中点, , 若 , , 求线段的长.(3)、【拓展提高】在中, , , 以为直角顶点作等腰直角 , 点在线段上,点在线段上.若 , 直接写出 .24. 如图,在平面直角坐标系中,抛物线 , 若抛物线与x轴交于 , 两点,与轴交于点 .
(1)、【基础巩固】如图,在中, , 是边上一点,是边上一点, . 求证: .(2)、【尝试应用】如图 , 在四边形中,点是边的中点, , 若 , , 求线段的长.(3)、【拓展提高】在中, , , 以为直角顶点作等腰直角 , 点在线段上,点在线段上.若 , 直接写出 .24. 如图,在平面直角坐标系中,抛物线 , 若抛物线与x轴交于 , 两点,与轴交于点 . (1)、求该抛物线的函数表达式;(2)、如图1,若点是直线下方的抛物线上一点,过点作 , 交轴于点 , 且 , 求点的横坐标;(3)、如图2,点在点的正下方,连接 , 交抛物线于点 , 直线交对称轴于点 , 作 , 交射线于点 , 求的大小.
(1)、求该抛物线的函数表达式;(2)、如图1,若点是直线下方的抛物线上一点,过点作 , 交轴于点 , 且 , 求点的横坐标;(3)、如图2,点在点的正下方,连接 , 交抛物线于点 , 直线交对称轴于点 , 作 , 交射线于点 , 求的大小.