湖北省武汉市实验初级中学2023-2024学年九年级下学期3月月考数学试题
试卷更新日期:2024-04-28 类型:月考试卷
一、选择题(共10小题,每小题3分,共30分)
-
1. 的相反数是( )A、 B、 C、 D、2. “篮球运动员投篮一次,投中篮筐”这一事件是( )A、不可能事件 B、必然事件 C、随机事件 D、确定事件3. 下面运动标识图案中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 下列运算正确的是( )A、 B、 C、 D、5. 如图是由5个大小相同的小正方体组成的几何体,它的俯视图( )
4. 下列运算正确的是( )A、 B、 C、 D、5. 如图是由5个大小相同的小正方体组成的几何体,它的俯视图( ) A、
A、 B、
B、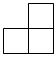 C、
C、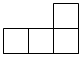 D、
D、 6. 已知点在反比例的数的图象上.其中.下列结论正确的是( )A、 B、 C、 D、7. 如图,某容器的底面水平放置,容器上下皆为圆柱形,且大圆柱的底面半径是小圆柱的底面半径的2倍,高度也是小圆柱的2倍,匀速地向此容器内注水,在注满水的过程中,水面的高度h与时间t的函数关系的图象如图所示,则灌满小圆柱时所需时间为( )
6. 已知点在反比例的数的图象上.其中.下列结论正确的是( )A、 B、 C、 D、7. 如图,某容器的底面水平放置,容器上下皆为圆柱形,且大圆柱的底面半径是小圆柱的底面半径的2倍,高度也是小圆柱的2倍,匀速地向此容器内注水,在注满水的过程中,水面的高度h与时间t的函数关系的图象如图所示,则灌满小圆柱时所需时间为( ) A、 B、 C、 D、108. 根据规定,我市将垃圾分为了四类:可回收物、易腐垃圾、有害垃圾和其他垃圾四大类. 现有投放这四类垃圾的垃圾桶各1个,若将用不透明垃圾袋分类打包好的两袋不同垃圾随机投进两个不同的垃圾桶,投放正确的概率是( )A、 B、 C、 D、9. 如图,AB为⊙O的直径,BC是弦,将绕着A点顺时针旋转得到 , 点D恰好落在⊙O上,AB交于E点,若OE=EB,AB=4,则BC的长是( )
A、 B、 C、 D、108. 根据规定,我市将垃圾分为了四类:可回收物、易腐垃圾、有害垃圾和其他垃圾四大类. 现有投放这四类垃圾的垃圾桶各1个,若将用不透明垃圾袋分类打包好的两袋不同垃圾随机投进两个不同的垃圾桶,投放正确的概率是( )A、 B、 C、 D、9. 如图,AB为⊙O的直径,BC是弦,将绕着A点顺时针旋转得到 , 点D恰好落在⊙O上,AB交于E点,若OE=EB,AB=4,则BC的长是( )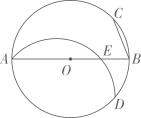 A、2 B、 C、 D、10. 定义:由a , b构造的二次函数叫做一次函数的“滋生函数”.若一次函数的“滋生函数”是 , t是关于x的方程的根,且 , 则的值为( )A、0 B、1 C、 D、
A、2 B、 C、 D、10. 定义:由a , b构造的二次函数叫做一次函数的“滋生函数”.若一次函数的“滋生函数”是 , t是关于x的方程的根,且 , 则的值为( )A、0 B、1 C、 D、二、填空题(共6小题,每小题3分,共18分)
-
11. 计算 的结果是.12. 太阳的半径约为696 000千米,用科学记数法表示数696 000为 .13. 计算的结果是 .14. 如图,有甲乙两座建筑物,从甲建筑物点处测得乙建筑物点的俯角为 , 点的俯角为 , 为两座建筑物的水平距离.已知乙建筑物的高度为 , 则甲建筑物的高度为.( , , , 结果保留整数).
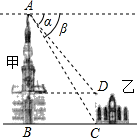 15. 已知抛物线( , a , b , c是常数)开口向上,过 , 两点(其中),下列四个结论:
15. 已知抛物线( , a , b , c是常数)开口向上,过 , 两点(其中),下列四个结论:①;
②若 , 则;
③对于任意实数t , 总有;
④关于x的一元二次方程必有两个不相等的数根.
其中正确的是(填写序号).
16. 在平面直角坐标系中, , , C在直线上运动,存在一点P , 满足 , 则的最小值为 .
三、解答题(共8小题,共72分)
-
17. 解不等式组请按下列步骤完成解答:(1)、解不等式①,得;(2)、解不等式②,得;(3)、将不等式①和②的解集在数轴上表示出来;
 (4)、原不等式组的解集为 .18. 如图, , , .
(4)、原不等式组的解集为 .18. 如图, , , . (1)、求的度数;(2)、若平分 , 求的度数.19. 在“4·23世界读书日”来临之际,某学校开展“让阅读成为习惯”的读书活动,为了解学生的参与程度,从全校随机抽取a名学生进行问卷调查,获取了每人平均每天阅读时间t(单位:分钟),将收集的数据分为A , B , C , D , E五个等级,绘制成如下不完整放计图表.
(1)、求的度数;(2)、若平分 , 求的度数.19. 在“4·23世界读书日”来临之际,某学校开展“让阅读成为习惯”的读书活动,为了解学生的参与程度,从全校随机抽取a名学生进行问卷调查,获取了每人平均每天阅读时间t(单位:分钟),将收集的数据分为A , B , C , D , E五个等级,绘制成如下不完整放计图表.平均每天阅读时间统计表
等级
人数
5
10
b
80
c

请根据图表中的信息,解答下列问题:
(1)、直接写出a , b的值;(2)、这组数据的中位数所在的等级是;(3)、学校拟将平均每天阅读时间不低于50分钟的学生评为“阅读达人”,若该校学生以2000人计算,估计可评为“阅读达人”的学生人数.20. 已知是的直径,C , D , E是半圆上三点,且 , . (1)、如图(1),求证:;(2)、如图(2),若 , , 求的值.21. 如图是由小正方形组成的网格,每个小正方形的顶点叫做格点.的三个顶点都是格点.仅用无刻度的直尺在给定网格中完成画图,画图过程用虚线表示.(1)、在图1中,已知格点O , 作的中点D , 过D作交于E , 画出线段;
(1)、如图(1),求证:;(2)、如图(2),若 , , 求的值.21. 如图是由小正方形组成的网格,每个小正方形的顶点叫做格点.的三个顶点都是格点.仅用无刻度的直尺在给定网格中完成画图,画图过程用虚线表示.(1)、在图1中,已知格点O , 作的中点D , 过D作交于E , 画出线段; (2)、在图2中,D是边上一点,先画点E , 使 , , 再在上画点F , 使 .
(2)、在图2中,D是边上一点,先画点E , 使 , , 再在上画点F , 使 . 22. 某市新建了一座室内滑雪场,该滑雪场地面积雪厚达 , 整个赛道长 , 全天共可容纳约3300人滑雪嬉戏.小明和小华相约去体验滑雪,小明从赛道顶端A处下滑,测得小明离A处的距离s(单位:m)随运动时间x(单位:s)变化的数据,整理得下表.
22. 某市新建了一座室内滑雪场,该滑雪场地面积雪厚达 , 整个赛道长 , 全天共可容纳约3300人滑雪嬉戏.小明和小华相约去体验滑雪,小明从赛道顶端A处下滑,测得小明离A处的距离s(单位:m)随运动时间x(单位:s)变化的数据,整理得下表.滑行时间x/s
0
1
2
3
4
滑行距离s/m
0
6
14
24
36
经验证小明离A处的距离s与运动时间x之间是二次函数关系.
小明出发的同时,小华在距赛道终点的B处操控一个无人机沿着赛道方向以的速度飞向小明,无人机离A处的距离y(单位:m)与运动时间x(单位:s)之间是一次函数关系.
 (1)、直接写出s关于x的函数解析式和y关于x的函数解析式(不要求写出自变量的取值范围);(2)、小明滑完整个赛道需要耗时多久?(3)、小明出发多久后与无人机相遇?23. 如图1,在中, , 为边上一点, .
(1)、直接写出s关于x的函数解析式和y关于x的函数解析式(不要求写出自变量的取值范围);(2)、小明滑完整个赛道需要耗时多久?(3)、小明出发多久后与无人机相遇?23. 如图1,在中, , 为边上一点, . (1)、求证:;(2)、如图2,过点作于 , 交于点 , 若 , 求的值;
(1)、求证:;(2)、如图2,过点作于 , 交于点 , 若 , 求的值; (3)、如图,为延长线上一点,连接 , 且 , 若直接写出的值(用含的代数式表示).
(3)、如图,为延长线上一点,连接 , 且 , 若直接写出的值(用含的代数式表示). 24. 如图,抛物线:与x轴交于 , 两点,与y轴交于点C.
24. 如图,抛物线:与x轴交于 , 两点,与y轴交于点C.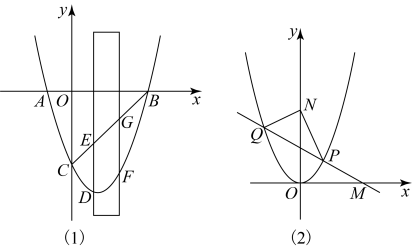 (1)、直接写出抛物线的解析式;(2)、如图(1),有一宽度为1的直尺平行于y轴,在点O,B之间平行移动,直尺两长边被线段和抛物线截得两线段 , .设点D的横坐标为t,且 , 试比较线段与的大小;(3)、如图(2),将抛物线平移得到顶点为原点的抛物线 , M是x轴正半轴上一动点,.经过点M的直线交抛物线于P,Q两点.当点M运动到某一个位置时,存在唯一的一条直线 , 使 , 求点M的坐标.
(1)、直接写出抛物线的解析式;(2)、如图(1),有一宽度为1的直尺平行于y轴,在点O,B之间平行移动,直尺两长边被线段和抛物线截得两线段 , .设点D的横坐标为t,且 , 试比较线段与的大小;(3)、如图(2),将抛物线平移得到顶点为原点的抛物线 , M是x轴正半轴上一动点,.经过点M的直线交抛物线于P,Q两点.当点M运动到某一个位置时,存在唯一的一条直线 , 使 , 求点M的坐标.