广东省深圳市2023-2024学年九年级下学期数学期中考试试卷

试卷更新日期：2024-04-28 类型：期中考试

进入出卷网下载

一、选择题（共10小题）

1. 如图是加工零件的尺寸要求，现有下列直径尺寸的产品（单位：mm），其中不合格的是（　　）

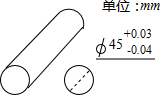A、Φ44.9 B、Φ45.02 C、Φ44.98 D、Φ45.01

查看试题解析
2. 第19届亚运会在浙江杭州举行，下列与杭州亚运会相关的图案中，是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 2022年10月12日下午，“天宫课堂”第三课在中国空间站开讲，神舟十四号飞行乘组三位航天员陈冬、刘洋、蔡旭哲进行授课，央视新闻抖音号进行全程直播，某一时刻观看人数达到421.1万，421.1万用科学记数法可以表示为（　　）

A、0.4211×10⁷ B、4.211×10⁶ C、421.1×10⁴ D、4211×10³

查看试题解析
4. 如图，分别在长方形ABCD的边DC，BC上取两点E，F，使得AE平分∠DAF，若∠BAF＝60°，则∠DAE＝(　　)

A、45° B、30° C、15° D、60°

查看试题解析
5. 在某次数学质量监测中，八年一班数学老师随机抽取了10份试卷，成绩表中所显示的分数如下：105，101，109，101，92，102，97，101，99，103，则这组数据的中位数是（）

A、101 B、 $96.5$ C、97 D、102

查看试题解析
6. 下列运算一定正确的是（）.

A、 $(m + n)^{2} = m^{2} + n^{2}$ B、 $(m n)^{3} = m^{3} n^{3}$ C、 $(m^{3})^{2} = m^{5}$ D、 $m • m^{2} = 2 m^{2}$

查看试题解析
7. 校园里一片小小的树叶，也蕴含着“黄金分割”，如图，P为AB的黄金分割点（AP＞PB），如果AB的长度为10cm ，那么AP的长度为（　　）cm ．

A、 $\sqrt{5} - 1$ B、 $2 \sqrt{5} - 2$ C、 $5 \sqrt{5} - 5$ D、 $10 \sqrt{5} - 10$

查看试题解析
8. 11月17日，2023年“全民健身日”系列活动——玉溪市健步走暨玉溪市职工“勤锻炼健康行”在玉溪高原体育运动中心举行，广大人民群众通过运动收获愉悦、收获健康、收获幸福．甲、乙两人沿着总长度为9千米的“健身步道”行走，甲的速度是乙的1.5倍，甲比乙提前15分钟走完全程，如果设乙的速度为x千米/时，那么下列方程中正确的是（　　）

A、 $\frac{9}{x} - \frac{9}{1.5 x} = 15$ B、 $\frac{9}{x} - \frac{9}{1.5 x} = \frac{1}{4}$ C、 $\frac{9}{1.5 x} - \frac{9}{x} = 15$ D、 $\frac{9}{1.5 x} - \frac{9}{x} = \frac{1}{4}$

查看试题解析
9. 如图，在平地上种植树木时，要求株距（相邻两棵树之间的水平距离）为5m ，若在坡比为i＝1：2.5的山坡种树，也要求株距为5m ，那么相邻两棵树间的坡面距离为（　　）

A、2.5m B、5m C、 $\sqrt{29} m$ D、10m

查看试题解析
10. 如图①，在正方形ABCD中，点E为DC边的中点，点P为线段BE上的一个动点．设BP＝x ， AP＝y ，图②是点P运动时y随x变化的关系图象，则正方形的周长为（　　）

A、 $4 \sqrt{5}$ B、8 C、 $8 \sqrt{2}$ D、10

查看试题解析

二、填空题（共5小题）

11. 新学期开始，小颖从学校开设的感兴趣的5门劳动教育课程：烹饪、茶艺、花卉种植、整理收纳、家电维修中，随机选择一门课程学习，她选择“茶艺”课程的概率是．

查看试题解析
12. 已知a+b=1，则代数式a²﹣b² +2b+9的值为.

查看试题解析
13. 如图，AB为⊙O的直径，点C在⊙O上，点P在线段OB上运动（不与O ， B重合），若∠CAB＝30°，设∠ACP为α，则α的取值范围是．

查看试题解析
14. 如图，D、E分别是△ABC的边上AB、BC上的点，DE∥AC ，若S_△_BDE：S_△_CDE＝1：3，当S_△_DOE＝1时，则S_△_AOC的值为．

查看试题解析
15. 如图所示，点A₁ ， A₂ ， A₃在x轴上且OA₁＝A₁A₂＝A₂A₃ ，分别过点A₁ ， A₂ ， A₃作y轴的平行线与反比例函数y $= \frac{k}{x}$ （k＞0，x＞0）的图象分别交于点B₁ ， B₂ ， B₃ ，分别过点B₁ ， B₂ ， B₃作x轴的平行线分别与y轴交于点C₁ ， C₂ ， C₃ ，连接OB₁ ， OB₂ ， OB₃ ，那么图中阴影部分的面积之和为．

查看试题解析

三、解答题（共7小题）

16. 计算： $2 s i n 6 0^{∘} + \sqrt{12} + | - 5 | - (π - \sqrt{2})^{0}$ ．

查看试题解析
17. 先化简，再求值： $(\frac{x^{2} - 4}{x^{2} - 4 x + 4} - \frac{1}{x - 2}) \cdot \frac{x^{2} - 2 x}{x + 1}$ ，其中x=5.

查看试题解析

18. 全球工业互联网大会永久会址落户沈阳．为了让学生了解工业互联网相关知识，某校准备开展“工业互联网”主题日活动，聘请专家为学生做五个领域的专题报告：A ．数字孪生；B ．人工智能；C ．应用5G；D ．工业机器人；E ．区块链．为了解学生的研学意向，在随机抽取的部分学生中下发如图所示的调查问卷，所有问卷全部收回且有效，根据调查数据绘制成两幅不完整的统计图．

“工业互联网”主题日学生研学意向调查问卷

请在下列选项中选择您的研学意向，并在其后“□”内打“√”（每名同学必选且只能选择其中一项），非常感谢您的合作．

A ．数字孪生□B ．人工智能□C ．应用5G□D ．工业机器人□E ．区块链□

请根据统计图提供的信息，解答下列问题：

(1)、本次调查所抽取的学生人数为，并直接补全条形统计图；

(2)、扇形统计图中领域“B”对应扇形的圆心角的度数为；

(3)、学校有600名学生参加本次活动，地点安排在两个多功能厅，每场报告时间为90分钟．由下面的活动日程表可知，A和C两场报告时间与场地已经确定．在确保听取报告的每名同学都有座位的情况下，请你合理安排B ， D ， E三场报告，补全此次活动日程表（写出一种方案即可），并说明理由．

“工业互联网”主题日活动日程表
地点（座位数）时间	1号多功能厅（200座）	2号多功能厅（100座）
8：00﹣9：30	① ▲	A
10：00﹣11：30	C	② ▲
13：00﹣14：30	③ ▲	设备检修暂停使用

查看试题解析

19. 家用电灭蚊器的发热部分使用了PTC发热材料，电阻R（单位：kΩ）随温度t（单位：℃）（在一定范围内）变化而变化，通电后该表记录了发热材料温度从上升到30℃的过程中，发现电阻与温度有如下关系：
t（℃）
5
10
15
20
30
R（kΩ）
12
6
4
3
2

(1)、根据表中的数据，在图中描出实数对（t ， R）的对应点，猜测并确定R与t之间的函数解析式并画出其图象；

(2)、当t≥30时，R与t间的函数解析式为 $R = \frac{4}{15} t - 6$ ．在图中画出该函数图象；

(3)、根据以上信息，家用电灭蚊器在使用过程中，温度在什么范围内发热材料的电阻不超过6kΩ．

查看试题解析
20. 列方程（组）或不等式（组）解应用题：学校为了支持体育社团开展活动，鼓励同学们加强锻炼，准备增购一些羽毛球拍和乒乓球拍．

(1)、根据图中信息，求出每支羽毛球拍和每支乒乓球拍的价格；

(2)、学校准备用5300元购买羽毛球拍和乒乓球拍，且乒乓球拍的数量为羽毛球拍数量的3倍，请问最多能购买多少支羽毛球拍？

查看试题解析

21.

根据背景素材，探索解决问题．

生活中的数学——自动旋转式洒水喷头如何灌溉草坪
背景素材	数学来源于生活，九4班分四个小组，开展数学项目式实践活动，获取所有数据共享，对草坪喷水管建立数学模型．草坪装有1个自动旋转式洒水喷头，灌溉园林草坪．如图1所示，观察喷头可顺、逆时针往返喷洒．

	甲小组在图2中建立合适的直角坐标系，喷水口中心O有一喷水管OA ，从A点向外喷水，喷出的水柱最外层的形状为抛物线．以水平方向为x轴，点O为原点建立平面直角坐标系，点A（喷水口）在y轴上，x轴上的点D为水柱的最外落水点．	乙小组在甲小组基础上，测量得距洒水喷头水平距离较远若干米的E处，正上方有一树枝叶F ，旋转式喷洒水柱外端刚好碰到树叶F的最低处．
	丙小组在甲小组基础上，测量得喷水口中心O到水柱的最外落水点D距离为半径，建立⊙O半径为OD的扇形平面图（图3）.
问题解决
任务1	获取数据	丁小组测量得喷头的高 $O A = \frac{2}{3}$ 米，喷水口中心点O到水柱的最外落水点D水平距离为8米，经过点 $(7, \frac{5}{4})$ ．
	解决问题	求出水柱所在抛物线的函数解析式．
任务2	获取数据	丁小组测树叶F距水平地面最低高度 $E F = \frac{13}{6}$ 米，点F在抛物线上且离水喷头水平距离较远，E在OD上，OD⊥EF ．
	解决问题	求OE的长．
任务3	推理计算	丁小组观察自动旋转式洒水喷头可顺、逆时针往返喷洒，可平面旋转角度不超过240°，求： ①这个喷头最多可洒水多少平方米？ ②在①条件下，此时DD^'的长．

查看试题解析

22.
例：如图1，在Rt△ABC中，∠ACB＝90°，
CD是斜边AB上的中线．求证：CD= $\frac{1}{2}$ AB ．
证明：延长CD至点E ，使DE＝CD ，连接AE ， BE ．
…

(1)、请根据教材提示，结合图1，写出完整的证明过程．

(2)、初步探究
如图2，在四边形ABCD中，∠BAD＝∠BCD＝90°，AB＝AD ， ∠CBD＝30°，AP⊥BD于点P ，连接CP ， $A C = \sqrt{3} + 1$
① ∠ACD的度数为．
②求AD长．

(3)、拓展运用
如图3，在平行四边形ABCD中，F是BC边上一点，∠ABC＝60°，BC＝6，BF＝2．按以下步骤作图：①以点B为圆心，以适当的长为半径作弧，分别交AB ， BC于点M ， N；②分别以点M ， N为圆心，大于 $\frac{1}{2} M N$ 的长为半径作弧，两弧交于点E ，作射线BE ．过点F作FP∥AB交BE于点P ，过点P作PG⊥AB于点G ， Q为射线BE上一动点，连接GQ ， CQ ，若 $P Q = \frac{1}{2} B P$ ，直接写出 $\frac{G Q}{C Q}$ 的值．

查看试题解析

t（℃）	5	10	15	20	30
R（kΩ）	12	6	4	3	2