浙江省丽水、湖州、衢州三地市2024届高三下学期4月二模数学试卷

试卷更新日期：2024-04-28 类型：高考模拟

进入出卷网下载

一、选择题

1. 掷两枚质地均匀的骰子，设A＝“第一枚出现奇数点”，B＝“第二枚出现偶数点”，则A与B的关系为（）

A、互斥 B、互为对立 C、相互独立 D、相等

查看试题解析
2. 双曲线 $x^{2} - \frac{y^{2}}{m^{2}} = 1 (m > 0)$ 的渐近线方程为 $y = \pm 2 x$ ，则 $m =$ ( )

A、 $\frac{1}{2}$ B、 $\frac{\sqrt{2}}{2}$ C、 $\sqrt{2}$ D、2

查看试题解析
3. 复数满足 $| i z | = 1$ (i为虚数单位)，则 $| z - 4 + 3 i |$ 的最小值是( )

A、3 B、4 C、5 D、6

查看试题解析
4. 已知平面向量 $\vec{a}$ ， $\vec{b}$ 满足 $| \vec{b} | = 2 | \vec{a} | = 2$ ，若 $\vec{a} ⊥ (\vec{a} + \vec{b})$ ，则 $\vec{a}$ 与 $\vec{b}$ 的夹角为( )

A、 $\frac{π}{6}$ B、 $\frac{5 π}{6}$ C、 $\frac{π}{3}$ D、 $\frac{2 π}{3}$

查看试题解析
5. 已知各项均为正数的等比数列 ${a_{n}}$ 的前n项和为 $S_{n}$ ，且满足 $a_{6}$ _， $3 a_{4}$ ， $- a_{5}$ 成等差数列，则 $\frac{S_{4}}{S_{2}} =$ ( )

A、3 B、9 C、10 D、13

查看试题解析
6. 将函数 $f (x) = c o s 2 x$ 的图象向右平移 $φ (0 < φ < \frac{π}{2})$ 个单位后得到函数 $g (x)$ 的图象，若对满足 $| f (x_{1}) - g (x_{2}) | = 2$ 的 $x_{1}$ ， $x_{2}$ ，有 ${| x_{1} - x_{2} |}_{m i n} = \frac{π}{3}$ ，则 $φ =$ ( )

A、 $\frac{π}{6}$ B、 $\frac{π}{4}$ C、 $\frac{π}{3}$ D、 $\frac{5 π}{12}$

查看试题解析
7. 已知椭圆 $C : \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ ， $F_{1}$ ， $F_{2}$ 为左､右焦点，P为椭圆上一点， $∠ F_{1} P F_{2} = 60 °$ ，直线 $l : y = - x + t$ 经过点P.若点 $F_{2}$ 关于l的对称点在线段 $F_{1} P$ 的延长线上，则C的离心率是( )

A、 $\frac{1}{3}$ B、 $\frac{\sqrt{2}}{2}$ C、 $\frac{1}{2}$ D、 $\frac{2}{3}$

查看试题解析
8. 已知正实数 $x_{1}$ ， $x_{2}$ ， $x_{3}$ 满足 $x_{1}^{2} + 2 x_{1} + 1 = x_{1} 2^{x_{1}}$ ， $x_{2}^{2} + 3 x_{2} + 1 = x_{2} 3^{x_{2}}$ ， $x_{3}^{2} + 4 x_{3} + 1 = x_{3} 4^{x_{3}}$ ，则 $x_{1}$ ， $x_{2}$ ， $x_{3}$ 的大小关系是( )

A、 $x_{3} < x_{2} < x_{1}$ B、 $x_{1} < x_{2} < x_{3}$ C、 $x_{1} < x_{3} < x_{2}$ D、 $x_{2} < x_{1} < x_{3}$

查看试题解析

二、多项选择题

9. 有一组样本数据 $x_{1}$ ， $x_{2}$ ， $x_{3}$ $x_{4}$ ， $x_{5}$ ， $x_{6}$ 的平均数是 $\bar{x}$ ，方差是 $s^{2}$ ，极差为R，则下列判断正确的是( )

A、若 $a x_{1} + b$ ， $a x_{2} + b$ ， $a x_{3} + b$ ， $a x_{4} + b$ ， $a x_{5} + b$ ， $a x_{6} + b$ 的平均数是 $\bar{x_{0}}$ ，则 $\bar{x_{0}} = a \bar{x} + b$ B、若 $x_{1}$ ， $2 x_{2}$ ， $3 x_{3}$ ， $4 x_{4}$ ， $5 x_{5}$ ， $6 x_{6}$ 的极差是 $R_{1}$ ，则 $R_{1} > R$ C、若方差 $s^{2} = 0$ ，则 $x_{1} = x_{2} = x_{3} = x_{4} = x_{5} = x_{6}$ D、若 $x_{1} < x_{2} < x_{3} < x_{4} < x_{5} < x_{6}$ ，则第75百分位数是 $\frac{x_{4} + x_{5}}{2}$

查看试题解析
10. 已知直三棱柱 $A B C - A_{1} B_{1} C_{1}$ 中， $A B ⊥ B C$ 且 $A B = B C = 2$ ，直线 $A_{1} C$ 与底面ABC所成角的正弦值为 $\frac{\sqrt{3}}{3}$ ，则( )

A、线段 $A_{1} C$ 上存在点D，使得 $A_{1} B ⊥ A D$ B、线段 $A_{1} C$ 上存在点D，使得平面 $D B B_{1} ⊥$ 平面 $D C C_{1}$ C、直三棱柱 $A B C - A_{1} B_{1} C_{1}$ 的体积为 $\frac{4}{3}$ D、点 $B_{1}$ 到平面 $A_{1} B C$ 的距离为 $\sqrt{2}$

查看试题解析
11. 已知函数 $f (x)$ 的定义域为R，且 $f (x + y) \cdot f (x - y) = f^{2} (x) - f^{2} (y)$ ， $f (1) = 2$ ， $f (x + 1)$ 为偶函数，则( )

A、 $f (3) = 2$ B、 $f (x)$ 为奇函数 C、 $f (2) = 0$ D、 $\sum_{k = 1}^{2024} f (k) = 0$

查看试题解析

三、填空题

12. 在 $△ A B C$ 中，角A，B，C的对边分别为a，b，c， $B = \frac{π}{4}$ ， $c = \sqrt{2}$ ， BC边上的高等于 $\frac{1}{3} a$ ，则 $△ A B C$ 的面积是， $s i n A =$ .

查看试题解析
13. 已知圆 $C : m x^{2} + (2 m - 1) y^{2} - 2 a x - a - 2 = 0$ ，若对于任意的 $a \in R$ ，存在一条直线被圆C所截得的弦长为定值n，则 $m + n =$ .

查看试题解析
14. 已知正四面体 $A - B C D$ 的棱长为1，若棱长为a的正方体能整体放入正四面体 $A - B C D$ 中，则实数a的最大值为.

查看试题解析

四、解答题

15. 设等差数列 ${a_{n}}$ 的公差为 $d$ ，记 $S_{n}$ 是数列 ${a_{n}}$ 的前n项和，若 $S_{5} = a_{3} + 20$ ， $S_{15} = a_{2} a_{3} a_{8}$ .

(1)、求数列 ${a_{n}}$ 的通项公式；

(2)、若 $d > 0, b_{n} = \frac{4 S_{n}}{a_{n} \cdot a_{n + 1}} (n \in N^{*})$ ，数列 ${b_{n}}$ 的前n项和为 $T_{n}$ ，求证： $T_{n} < n + \frac{1}{2}$ .

查看试题解析
16. 如图，三棱锥 $A - B C D$ 中， $A D ⊥ C D$ ， $A D = C D$ ， $∠ A D B = ∠ B D C$ ， E为线段AC的中点.

(1)、证明：平面 $B E D ⊥$ 平面ACD；

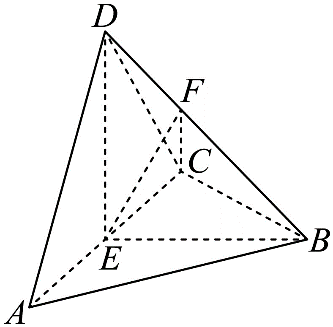(2)、设 $A B = B D = 3$ ， $\vec{B F} = 2 \vec{F D}$ ， $\vec{E F} \cdot \vec{B D} = 0$ ，求直线CF与平面ABC所成角的正弦值.

查看试题解析
17. 设函数 $f (x) = e^{x} - l n (x + a)$ ， $a \in R$ .

(1)、当 $a = 1$ 时，求函数 $f (x)$ 的单调区间；

(2)、若对定义域内任意的实数x，恒有 $f (x) \geq a$ ，求实数a的取值范围.(其中 $e \approx 2.71828$ 是自然对数的底数)

查看试题解析
18. 已知抛物线 $E : y^{2} = 4 x$ ，点A，B，C在抛物线E上，且A在x轴上方，B和C在x轴下方(B在C左侧)，A，C关于x轴对称，直线AB交x轴于点M，延长线段CB交x轴于点Q，连接QA.

(1)、证明： $\frac{| O M |}{| O Q |}$ 为定值(O为坐标原点)；

(2)、若点Q的横坐标为 $- 1$ ，且 $\vec{M B} \cdot \vec{M C} = \frac{8}{9}$ ，求 $△ A Q B$ 的内切圆的方程.

查看试题解析
19. 为保护森林公园中的珍稀动物，采用某型号红外相机监测器对指定区域进行监测识别.若该区域有珍稀动物活动，该型号监测器能正确识别的概率(即检出概率)为 $p_{1}$ ；若该区域没有珍稀动物活动，但监测器认为有珍稀动物活动的概率(即虚警概率)为 $p_{2}$ .已知该指定区域有珍稀动物活动的概率为0.2.现用2台该型号的监测器组成监测系统，每台监测器(功能一致)进行独立监测识别，若任意一台监测器识别到珍稀动物活动，则该监测系统就判定指定区域有珍稀动物活动.

(1)、若 $p_{1} = 0.8$ ， $p_{2} = 0.02$ .
①在该区域有珍稀动物活动的条件下，求该监测系统判定指定区域有珍稀动物活动的概率；
②在判定指定区域有珍稀动物活动的条件下，求指定区域实际没有珍稀动物活动的概率(精确到0.001)；

(2)、若监测系统在监测识别中，当 $0.8 \leq p_{1} \leq 0.9$ 时，恒满足以下两个条件：
①若判定有珍稀动物活动时，该区域确有珍稀动物活动的概率至少为0.9；
②若判定没有珍稀动物活动时，该区域确实没有珍稀动物活动的概率至少为0.9.求 $p_{2}$ 的范围(精确到0.001).
(参考数据： $\frac{\sqrt{35.04}}{6} = 0.9866, \frac{\sqrt{35.01}}{6} = 0.9861, 0.9 8^{2} = 0.9604$ )

查看试题解析