【北师大版·数学】2024年中考二轮复习之三角形
试卷更新日期:2024-04-28 类型:二轮复习
一、选择题
-
1. 如图,用尺规作图作∠BAC的平分线AD , 第一步是以A为圆心,任意长为半径画弧,分别交AB , AC于点E , F;第二步是分别以E , F为圆心,以大于 EF长为半径画弧,两圆弧交于D点,连接AD , AD即为所求作,请说明△AFD≌△AED的依据是( )
 A、SSS B、SAS C、ASA D、AAS2. 在测量一个小口圆柱形容器的壁厚时,小明用“X型转动钳”按如图方法进行测量,其中OA=OD,OB=OC,CD为直径,测得AB=a,EF=b,则圆柱形容器的壁厚是( )
A、SSS B、SAS C、ASA D、AAS2. 在测量一个小口圆柱形容器的壁厚时,小明用“X型转动钳”按如图方法进行测量,其中OA=OD,OB=OC,CD为直径,测得AB=a,EF=b,则圆柱形容器的壁厚是( ) A、a B、b C、b-a D、(b-a)3. 如图,用尺规作角平分线,根据作图步骤,在说明射线AN是∠BAC的平分线过程中,以下说法错误的是( )
A、a B、b C、b-a D、(b-a)3. 如图,用尺规作角平分线,根据作图步骤,在说明射线AN是∠BAC的平分线过程中,以下说法错误的是( ) A、由作弧可知AE=AF B、由作弧可知FP=EP C、由SAS 证明△AFP≌△AEP D、由SSS证明△AFP≌△AEP4. 尺规作图作角的平分线,作法步骤如下:
A、由作弧可知AE=AF B、由作弧可知FP=EP C、由SAS 证明△AFP≌△AEP D、由SSS证明△AFP≌△AEP4. 尺规作图作角的平分线,作法步骤如下:①以点O为圆心,任意长为半径画弧,交OA、OB于C、D两点;
②分别以C、D为圆心,大于 CD长为半径画弧,两弧交于点P;
③过点P作射线OP , 射线OP即为所求.

则上述作法的依据是( )
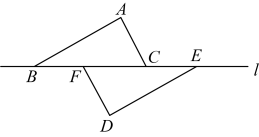
A、SSS B、SAS C、AAS D、ASA5. 如图,点C , F , B , E在同一直线上,∠C=∠DFE=90°,添加下列条件,仍不能判定△ACB与△DFE全等的是( ) A、∠A=∠D , AB=DE B、AC=DF , CF=BE C、AB=DE , BC=EF D、∠A=∠D , ∠ABC=∠E6. 如图,四边形 是菱形, 、 分别是 、 两边上的点不能保证 和 一定全等的条件是( )
A、∠A=∠D , AB=DE B、AC=DF , CF=BE C、AB=DE , BC=EF D、∠A=∠D , ∠ABC=∠E6. 如图,四边形 是菱形, 、 分别是 、 两边上的点不能保证 和 一定全等的条件是( ) A、 B、 C、 D、7. 一把直尺与30°的直角三角板如图所示,∠1=40°,则∠2=( )
A、 B、 C、 D、7. 一把直尺与30°的直角三角板如图所示,∠1=40°,则∠2=( ) A、50° B、60° C、70° D、80°8. 如图,已知D、E、F分别是等边△ABC的边AB、BC、AC上的点,且DE⊥BC、EF⊥AC、FD⊥AB , 则下列结论不成立的是( )
A、50° B、60° C、70° D、80°8. 如图,已知D、E、F分别是等边△ABC的边AB、BC、AC上的点,且DE⊥BC、EF⊥AC、FD⊥AB , 则下列结论不成立的是( )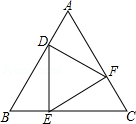 A、△DEF是等边三角形 B、△ADF≌△BED≌△CFE C、DE=
A、△DEF是等边三角形 B、△ADF≌△BED≌△CFE C、DE=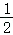 AB
D、S△ABC=3S△DEF
9. 如图,已知∠ABC=∠DCB,下列所给条件不能证明△ABC≌△DCB的是( )
AB
D、S△ABC=3S△DEF
9. 如图,已知∠ABC=∠DCB,下列所给条件不能证明△ABC≌△DCB的是( )
A、∠A=∠D B、AB=DC C、∠ACB=∠DBC D、AC=BD10. 如图,已知∠MAN=55°,点B为AN上一点.用尺规按如下过程作图:以点A为圆心,以任意长为半径作弧,交AN于点D,交AM于点E;以点B为圆心,以AD为半径作弧,交AB于点F;以点F为圆心,以DE为半径作弧,交前面的弧于点G;连接BG并延长交AM于点C.则∠BCM的度数为( )
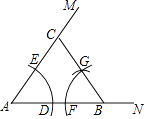 A、70° B、110° C、125° D、130°
A、70° B、110° C、125° D、130°二、填空题
-
11. 如图,在 中, , ,点D是边AB上一点,点B关于直线CD的对称点为 ,当 时,则 的度数为 .
 12. 如图, , 若 , , 则=度.
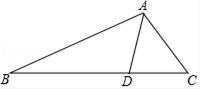
12. 如图, , 若 , , 则=度. 13. 如图,在△ABC中,AD⊥BC于点D,AD与BE相交于点F,且AC=BF,DF=DC.若∠ABE=10°,则∠DBF的度数为 .
13. 如图,在△ABC中,AD⊥BC于点D,AD与BE相交于点F,且AC=BF,DF=DC.若∠ABE=10°,则∠DBF的度数为 .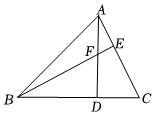 14. 如图,在 中, 平分 , ,垂足为 , 为 的中点.若 , ,则 的长为 .
14. 如图,在 中, 平分 , ,垂足为 , 为 的中点.若 , ,则 的长为 . 15. 如图,AB是一座办公大楼,一架无人机从C处测得楼顶部B的仰角为60°,测得楼底部A的俯角为37°,测得与大楼的水平距离为40米,则该办公大楼的高度是米.(结果保留整数,参考数据: ≈1.73,sin37°≈0.6,cos37°≈0.8,tan37°≈0.75)
15. 如图,AB是一座办公大楼,一架无人机从C处测得楼顶部B的仰角为60°,测得楼底部A的俯角为37°,测得与大楼的水平距离为40米,则该办公大楼的高度是米.(结果保留整数,参考数据: ≈1.73,sin37°≈0.6,cos37°≈0.8,tan37°≈0.75)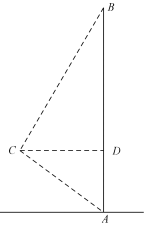
三、解答题
-
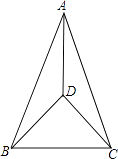
16. 如图,在△ABC中,AB=AC,AD平分∠BAC.求证:∠DBC=∠DCB.
 17. 如图,点E,F在AB上,AD=BC,∠A=∠B,AE=BF.求证:△ADF≌△BCE.
17. 如图,点E,F在AB上,AD=BC,∠A=∠B,AE=BF.求证:△ADF≌△BCE.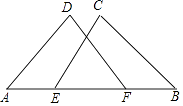 18. 如图, , , , 求的长.
18. 如图, , , , 求的长.
四、作图题
-
19. 尺规作图:
已知:∠AOB.
求作:射线OC,使它平分∠AOB.
作法:
①以O为圆心,任意长为半径作弧,交OA于D,交OB于E;
②分别以D、E为圆心,大于 DE的同样长为半径作弧,两弧相交于点C;
③作射线OC.
所以射线OC就是所求作的射线.
(1)、使用直尺和圆规,补全图形;(保留作图痕迹)(2)、完成下面的证明.证明:连结CE,CD.
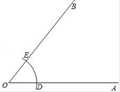
∵OE=OD,= , OC=OC,
∴△OEC≌△ODC(依据:),
∴∠EOC=∠DOC,
即OC平分∠AOB.
20. 如图,在矩形ABCD中, (1)、尺规作图:作 于点F; 保留作图痕迹,不写作法(2)、求证: .
(1)、尺规作图:作 于点F; 保留作图痕迹,不写作法(2)、求证: .五、综合题