【北师大版·数学】2024年中考二轮复习之函数基础知识
试卷更新日期:2024-04-28 类型:二轮复习
一、选择题
-
1. 如图1,在中,动点P从A点运动到B点再到C点后停止,速度为2单位/s,其中长与运动时间t(单位:s)的关系如图2,则的长为( )
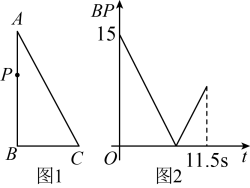 A、 B、 C、17 D、2. 如图,△ABC为直角三角形,∠C=90°,BC=2cm,∠A=30°,四边形DEFG为矩形,DE=2cm,EF=6cm,且点C、B、E、F在同一条直线上,点B与点E重合.Rt△ABC以每秒1cm的速度沿矩形DEFG的边EF向右平移,当点C与点F重合时停止.设Rt△ABC与矩形DEFG的重叠部分的面积为ycm2 , 运动时间xs.能反映ycm2与xs之间函数关系的大致图象是( )
A、 B、 C、17 D、2. 如图,△ABC为直角三角形,∠C=90°,BC=2cm,∠A=30°,四边形DEFG为矩形,DE=2cm,EF=6cm,且点C、B、E、F在同一条直线上,点B与点E重合.Rt△ABC以每秒1cm的速度沿矩形DEFG的边EF向右平移,当点C与点F重合时停止.设Rt△ABC与矩形DEFG的重叠部分的面积为ycm2 , 运动时间xs.能反映ycm2与xs之间函数关系的大致图象是( )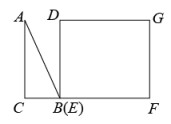 A、
A、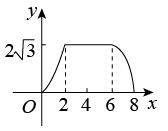 B、
B、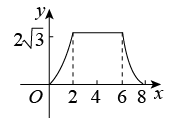 C、
C、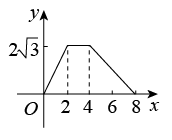 D、
D、 3. 如图,菱形ABCD的边长为2cm,其中∠A=60°,动点E,F同时从点A都以1cm/s的速度出发,点E沿A→B→C路线,点F沿A→D→C路线运动。连接EF.设运动时间为ts,△AEF的面积为Scm2 , 则下列图象中能大致表示S与t的函数关系的是( )
3. 如图,菱形ABCD的边长为2cm,其中∠A=60°,动点E,F同时从点A都以1cm/s的速度出发,点E沿A→B→C路线,点F沿A→D→C路线运动。连接EF.设运动时间为ts,△AEF的面积为Scm2 , 则下列图象中能大致表示S与t的函数关系的是( )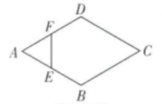 A、
A、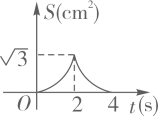 B、
B、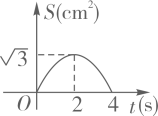 C、
C、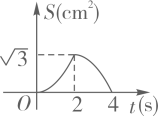 D、
D、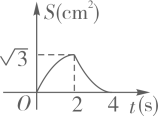 4. 如图1,在菱形ABCD中,AB=6,∠BAD=120°,点E是BC边上的一动点,点P是对角线BD上一动点,设PD的长度为x,PE与PC的长度和为y,图2是y关于x的函数图象,其中H(a,b)是图象上的最低点,则a+b的值为( )
4. 如图1,在菱形ABCD中,AB=6,∠BAD=120°,点E是BC边上的一动点,点P是对角线BD上一动点,设PD的长度为x,PE与PC的长度和为y,图2是y关于x的函数图象,其中H(a,b)是图象上的最低点,则a+b的值为( ) A、 B、 C、 D、365. 如图,已知A , B是反比例函数y= (k>0,x>0)图象上的两点,BC∥x轴,交y轴于点C , 动点P从坐标原点O出发,沿O→A→B→C(图中“→”所示路线)匀速运动,终点为C , 过P作PM⊥x轴,垂足为M . 设三角形OMP的面积为S , P点运动时间为t , 则S关于t的函数图象大致为( )
A、 B、 C、 D、365. 如图,已知A , B是反比例函数y= (k>0,x>0)图象上的两点,BC∥x轴,交y轴于点C , 动点P从坐标原点O出发,沿O→A→B→C(图中“→”所示路线)匀速运动,终点为C , 过P作PM⊥x轴,垂足为M . 设三角形OMP的面积为S , P点运动时间为t , 则S关于t的函数图象大致为( )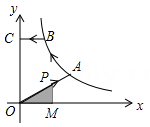 A、
A、 B、
B、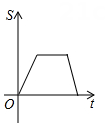 C、
C、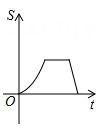 D、
D、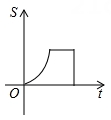 6. 如图,边长分别为1和2的两个等边三角形,开始它们在左边重合,大三角形固定不动,然后把小三角形自左向右平移直至移出大三角形外停止.设小三角形移动的距离为x,两个三角形重叠面积为y,则y关于x的函数图象是( )
6. 如图,边长分别为1和2的两个等边三角形,开始它们在左边重合,大三角形固定不动,然后把小三角形自左向右平移直至移出大三角形外停止.设小三角形移动的距离为x,两个三角形重叠面积为y,则y关于x的函数图象是( )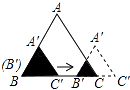 A、
A、 B、
B、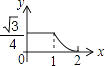 C、
C、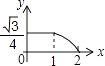 D、
D、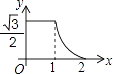 7.
7.某星期下午,小强和同学小明相约在某公共汽车站一起乘车回学校,小强从家出发先步行到车站,等小明到了后两人一起乘公共汽车回到学校.图中折线表示小强离开家的路程y(公里)和所用的时间x(分)之间的函数关系.下列说法错误的是( )
 A、小强从家到公共汽车在步行了2公里 B、小强在公共汽车站等小明用了10分钟 C、公共汽车的平均速度是30公里/小时 D、小强乘公共汽车用了20分钟8.
A、小强从家到公共汽车在步行了2公里 B、小强在公共汽车站等小明用了10分钟 C、公共汽车的平均速度是30公里/小时 D、小强乘公共汽车用了20分钟8.如图,在等腰△ABC中,直线l垂直底边BC,现将直线l沿线段BC从B点匀速平移至C点,直线l与△ABC的边相交于E、F两点.设线段EF的长度为y,平移时间为t,则下图中能较好反映y与t的函数关系的图象是( )
 A、
A、 B、
B、 C、
C、 D、
D、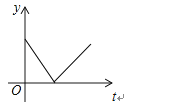 9.
9.如图,在矩形中截取两个相同的正方形作为立方体的上下底面,剩余的矩形作为立方体的侧面,刚好能组成立方体.设矩形的长和宽分别为y和x,则y与x的函数图象大致是( )
 A、
A、 B、
B、 C、
C、 D、
D、 10. 如图,在直角三角形ABC中,∠C=90°,AC=BC,E是AB的中点,过点E作AC和BC的垂线,垂足分别为点D和点F,四边形CDEF沿着CA方向匀速运动,点C与点A重合时停止运动,设运动时间为t,运动过程中四边形CDEF与△ABC的重叠部分面积为S.则S关于t的函数图象大致为( )
10. 如图,在直角三角形ABC中,∠C=90°,AC=BC,E是AB的中点,过点E作AC和BC的垂线,垂足分别为点D和点F,四边形CDEF沿着CA方向匀速运动,点C与点A重合时停止运动,设运动时间为t,运动过程中四边形CDEF与△ABC的重叠部分面积为S.则S关于t的函数图象大致为( )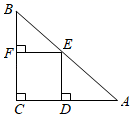 A、
A、 B、
B、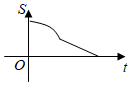 C、
C、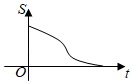 D、
D、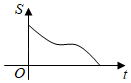
二、填空题
-
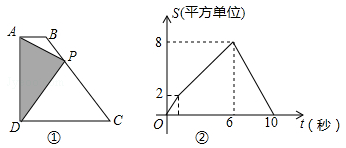
11. 定义: ,例如: , ,当 时,函数 的最小值为 .12. 如图①,四边形ABCD中,AB∥CD,∠ADC=90°,P从A点出发,以每秒1个单位长度的速度,按A→B→C→D的顺序在边上匀速运动,设P点的运动时间为t秒,△PAD的面积为S,S关于t的函数图象如图②所示,当P运动到BC中点时,△PAD的面积为 .
 13. 在函数y= 中,自变量x的取值范围是14. 小华和小兰两家相距2400米,他们相约到两家之间的剧院看戏,两人同时从家出发匀速前行,出发15分钟后,小华发现忘带门票,立即以原来速度的1.5倍返回家中,取完东西后仍以返回时的速度去见小兰;而小兰在出发30分钟时到达剧院,等待10分钟后未见小华,于是仍以原来的速度,从剧院出发前往小华家,途中两人相遇.假设小华掉头、取票时间均忽略不计.两人之间的距离y(米)与小华出发时间x(分钟)之间的关系如图所示,则当两人相遇时,小兰距离剧院有 米.
13. 在函数y= 中,自变量x的取值范围是14. 小华和小兰两家相距2400米,他们相约到两家之间的剧院看戏,两人同时从家出发匀速前行,出发15分钟后,小华发现忘带门票,立即以原来速度的1.5倍返回家中,取完东西后仍以返回时的速度去见小兰;而小兰在出发30分钟时到达剧院,等待10分钟后未见小华,于是仍以原来的速度,从剧院出发前往小华家,途中两人相遇.假设小华掉头、取票时间均忽略不计.两人之间的距离y(米)与小华出发时间x(分钟)之间的关系如图所示,则当两人相遇时,小兰距离剧院有 米.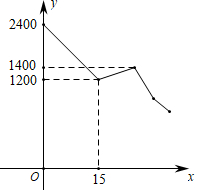 15. 在函数y= 中,自变量x的取值范围是 .
15. 在函数y= 中,自变量x的取值范围是 .三、实践探究题
-
16. 如图,甲、乙分别从A(-9,0),B(13,0)两点同时出发,甲朝着正北方向,以每秒3个单位长度的速度运动;乙朝着正西方向,以每秒4个单位长度的速度运动.设运动时间为t秒.
规定:t秒时,甲到达的位置记为点A,乙到达的位置记为点B,例如,1秒时,甲到达的位置记为A,乙到达的位置记为B,(如图所示);2.5秒时,甲到达的位置记为A2.5等等.容易知道,两条平行且相等的线段,其中包含有相同的方位信息所以,在研究有关运动问题时,为研究方便,我们可把点或线段进行合适的平移后,再去研究(物理上的相对运动观,就是源于这种数学方法)现对t秒时,甲、乙到达的位置点At , Bt , 按如下步骤操作:
第一步:连接AtBt;
第二步:把线段AtBt进行平移,使点Bt与点B重合,平移后,点A1的对应点用点At’标记
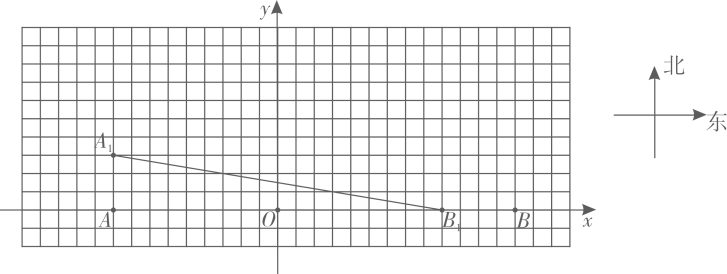
解答下列问题:
(1)、[理解与初步应用]
当t=1时,①利用网格,在上图中画出A1 , B1经过上述第二步操作后的图形;
②此时,甲在乙的什么方位?(请填空)
答:此时,甲在乙的北偏西θ°(其中tanθ°= , 两者相距 个单位长度.
(2)、[实验与数据整理]
补全下表:t的取值
1
2
3
t
点At'的坐标
(-5,3)
( , )
( , )
( , )
(3)、[数据分析与结论运用]①如果把点At'的横、纵坐标分别用变量x,y表示,则y与x之间的函数关系式为;
②点A3.5’的坐标为
(4)、[拓展应用]
我们知道,在运动过程中的任意时刻t,甲相对于乙的方位(即,点At相对于点Bt的方位)与At'相对于点B的方位相同.这为我们解决某些问题,提供了新思路.请解答:运动过程中,甲、乙之间的最近距离为个单位长度.
17. 【探究函数的图象与性质】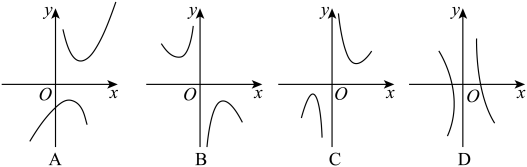 (1)、函数的自变量x的取值范围是;(2)、下列四个函数图象中,函数的图象大致是;(3)、对于函数 , 求当时,y的取值范围.请将下列的求解过程补充完整.
(1)、函数的自变量x的取值范围是;(2)、下列四个函数图象中,函数的图象大致是;(3)、对于函数 , 求当时,y的取值范围.请将下列的求解过程补充完整.解:∵ , ∴ .
∵ , ∴ .
(4)、【拓展说明】若函数 , 求y的取值范围.
四、综合题
-
18. 在并联电路中,电源电压为 , 小亮根据“并联电路分流不分压”的原理知道:( , ).已知R1为定值电阻,当R变化时,干路电流也会发生变化,且干路电流与R之间满足如下关系: .
 (1)、定值电阻的阻值为;(2)、小亮根据学习函数的经验,参照研究函数的过程与方法,对比反比例函数来探究函数的图象与性质.
(1)、定值电阻的阻值为;(2)、小亮根据学习函数的经验,参照研究函数的过程与方法,对比反比例函数来探究函数的图象与性质.①列表:下表列出点与R的几组对应值,请写出m,n的值: , ;
R
…
3
4
5
6
…
…
2
1.5
1.2
1
…
…
3
m
2.2
n
…
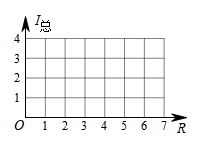
②描点、连线:在平面直角坐标系中,以①给出的R的取值为横坐标,以相对应的值为纵坐标,描出相应的点,并将各点用光滑曲线顺次连接起来 ;
(3)、观察图象并分析表格,回答下列问题:①随R的增大而;(填“增大”或“减小”)
②函数的图象是由的图象向平移个单位而得到.
19. 某学校STEAM社团在进行项目化学习时,根据古代的沙漏模型(图1)制作了一套“沙漏计时装置”,该装置由沙漏和精密电子秤组成,电子秤上放置盛沙容器.沙子缓慢匀速地从沙漏孔漏到精密电子称上的容器内,可以通过读取电子秤的读数计算时间(假设沙子足够).该实验小组从函数角度进行了如下实验探究:实验观察:实验小组通过观察,每两小时记录一次电子秤读数,得到下表.
漏沙时间x(h)
0
2
4
6
8
电子秤读数y(克)
6
18
30
42
54
 (1)、探索发现:建立平面直角坐标系,如图2,横轴表示漏沙时间x,纵坐标表示精密电子称的读数y,描出以表中的数据为坐标的各点.(2)、观察上述各点的分布规律,判断它们是否在同一条直线上,如果在同一条直线上,请你建立适当的函数模型,并求出函数表达式,如果不在同一条直线上,请说明理由.(3)、结论应用:应用上述发现的规律估算:若漏沙时间为9小时,精密电子称的读数为多少?(4)、若本次实验开始记录的时间是上午7:30,当精密电子秤的读数为72克时是几点钟?20. 在并联电路中,电源电压为 ,小亮根据“并联电路分流不分压”的原理知道: ( , ).已知R1为定值电阻,当R变化时,干路电流 也会发生变化,且干路电流 与R之间满足如下关系: .
(1)、探索发现:建立平面直角坐标系,如图2,横轴表示漏沙时间x,纵坐标表示精密电子称的读数y,描出以表中的数据为坐标的各点.(2)、观察上述各点的分布规律,判断它们是否在同一条直线上,如果在同一条直线上,请你建立适当的函数模型,并求出函数表达式,如果不在同一条直线上,请说明理由.(3)、结论应用:应用上述发现的规律估算:若漏沙时间为9小时,精密电子称的读数为多少?(4)、若本次实验开始记录的时间是上午7:30,当精密电子秤的读数为72克时是几点钟?20. 在并联电路中,电源电压为 ,小亮根据“并联电路分流不分压”的原理知道: ( , ).已知R1为定值电阻,当R变化时,干路电流 也会发生变化,且干路电流 与R之间满足如下关系: . (1)、定值电阻 的阻值为 ;(2)、小亮根据学习函数的经验,参照研究函数的过程与方法,对比反比例函数 来探究函数 的图象与性质.
(1)、定值电阻 的阻值为 ;(2)、小亮根据学习函数的经验,参照研究函数的过程与方法,对比反比例函数 来探究函数 的图象与性质.①列表:下表列出 点与R的几组对应值,请写出m,n的值: , ;
R
…
3
4
5
6
…
…
2
1.5
1.2
1
…
…
3
m
2.2
n
…

②描点、连线:在平面直角坐标系中,以①给出的R的取值为横坐标,以 相对应的值为纵坐标,描出相应的点,并将各点用光滑曲线顺次连接起来;
(3)、观察图象并分析表格,回答下列问题:① 随R的增大而;(填“增大”或“减小”)
②函数 的图象是由 的图象向平移个单位而得到.
21. 已知点A(2,a)、B(﹣8,b)两点在函数y=的图象上. (1)、直接写出a= , b= , 并在网格内画出函数y=的图象;(2)、将点C(6,c)绕A点逆时针旋转90°得到点D,若点D恰好落在函数图象上,求c的值;(3)、设AB的解析式为y=kx+m,请直接写出不等式kx+m>的解集.22. 九年级某数学兴趣小组在学习了反比例函数的图象与性质后,进一步研究了函数的图象与性质,其探究过程如下:(1)、绘制函数图象,
(1)、直接写出a= , b= , 并在网格内画出函数y=的图象;(2)、将点C(6,c)绕A点逆时针旋转90°得到点D,若点D恰好落在函数图象上,求c的值;(3)、设AB的解析式为y=kx+m,请直接写出不等式kx+m>的解集.22. 九年级某数学兴趣小组在学习了反比例函数的图象与性质后,进一步研究了函数的图象与性质,其探究过程如下:(1)、绘制函数图象,列表:下表是x与y的几组对应值,其中m= .
x
…
﹣3
﹣2
﹣1
1
2
3
…
y
…
1
2
4
4
2
1
m
…
描点:根据表中各组对应值(x,y),在平面直角坐标系中描出各点,请你描出剩下的点;
连线:用平滑的曲线顺次连接各点,已经画出了部分图象,请你把图象补充完整;
 (2)、通过观察图象,下列关于该函数的性质表述正确的是:;(填写代号)
(2)、通过观察图象,下列关于该函数的性质表述正确的是:;(填写代号)①函数值y随x的增大而增大;②关于y轴对称;③关于原点对称;
(3)、在上图中,若直线y=2交函数的图象于A,B两点(A在B左边),连接OA.过点B作BCOA交x轴于C.则= .