【北师大版·数学】2024年中考二轮复习之整式的乘除

试卷更新日期：2024-04-28 类型：二轮复习

进入出卷网下载

一、选择题

1. 已知 $9^{m} = 3 ， 27^{n} = 4$ ，则 $3^{2 m + 3 n} =$ （）

A、1 B、6 C、7 D、12

查看试题解析
2. 如图①，从边长为a的正方形中剪去一个边长为b的小正方形，然后将剩余分剪拼成一个长方形（如图②），则上述操作所能验证的公式是（）

A、 $a^{2} + a b = a (a + b)$ B、 ${(a - b)}^{2} = a^{2} - 2 a b + b^{2}$ C、 ${(a + b)}^{2} = a^{2} + 2 a b + b^{2}$ D、 $a^{2} - b^{2} = (a + b) (a - b)$

查看试题解析
3. 计算 ${(\frac{1}{3})}^{- 2}$ 的结果是（）

A、﹣9 B、9 C、 $\frac{1}{9}$ D、－ $\frac{1}{9}$

查看试题解析
4. 下列计算正确的是（）

A、 $a^{2} + a^{3} = a^{5}$ B、 ${(2 a)}^{2} = 4 a$ C、 $a^{2} \cdot a^{3} = a^{6}$ D、 ${(a^{2})}^{3} = a^{6}$

查看试题解析
5. 下列运算正确的是（）

A、 ${(- a)}^{3} = a^{3}$ B、 ${(x - y)}^{2} = x^{2} - y^{2}$ C、 ${(a^{2})}^{3} = a^{3}$ D、 $(b + a) (b - a) = b^{2} - a^{2}$

查看试题解析
6. 下列运算正确的是（）

A、 $a^{3} \cdot a^{2} = a^{6}$ B、 $4 a b - a b = 4$ C、 ${(a + 1)}^{2} = a^{2} + 1$ D、 ${(- a^{3})}^{2} = a^{6}$

查看试题解析
7. 2021年11月6日，台积电宣称2025年将量产2纳米芯片，2纳米就是0.000000002米，数据0.000000002用科学记数法表示是（）

A、 $2 \times 1 0^{9}$ B、 $2 \times 1 0^{- 9}$ C、 $0.2 \times 1 0^{- 8}$ D、 $2 \times 1 0^{- 8}$

查看试题解析
8. 下列运算正确的是（）

A、 $(\sqrt{2023} + \sqrt{23}) (\sqrt{2023} - \sqrt{23}) = 2000$ B、 $\frac{1}{\sqrt{5} - 2} = 2 - \sqrt{5}$ C、 $- a b \cdot (a b^{3}) = - a^{4} b^{4}$ D、 $(- 1)^{- 1} = 1$

查看试题解析
9. 下列计算正确的是（）

A、a²•a⁶＝a12 B、a⁸÷a⁴＝a² C、(−2a²)³=−8a⁶ D、a³+a⁴＝a⁷

查看试题解析
10. 计算 $202 2^{0}$ 的结果是（）

A、1 B、0 C、2022 D、 $\frac{1}{2022}$

查看试题解析

二、填空题

11. 若□ $× 2 x y = 4 x^{2} y^{2}$ ，则□内应填的单项式是．

查看试题解析
12. 计算： $3 x \cdot (2 x^{2} - y) =$ ．

查看试题解析
13. 计算： ${(\frac{1}{3})}^{- 1} =$ .

查看试题解析
14. 若非零实a，b满足a²＝ab $- \frac{b^{2}}{4}$ ，即可得 $- \frac{b}{a}$ 的值为．

查看试题解析
15. 实践操作：现有两个正方形A，B．如图所示进行两种方式摆放：
方式1：将B放在A的内部，得甲图；
方式2：将A，B并列放置，构造新正方形得乙图．
问题解决：对于上述操作，若甲图和乙图阴影部分的面积分别为1和12，则正方形A，B的面积之和为．

查看试题解析

三、计算题

16. 利用乘法公式计算：

(1)、 $32 5^{2} - 27 5^{2}$ ；

(2)、 $295 \times 305 - 29 8^{2}$ ．

查看试题解析
17. 先化简，再求值：（x+1）（x﹣1）+（2﹣x）x，其中 $x = \frac{3 \sqrt{2}}{2}$ ．

查看试题解析
18. 计算：

(1)、|﹣2|+（﹣2）²+（3.14﹣π）⁰﹣（ $\frac{1}{3}$ ）^﹣1 ．

(2)、（﹣2x）³÷x﹣（﹣x）² ．

查看试题解析

四、解答题

19. 如图 $①$ ，从边长为 $a$ 的正方形中剪掉一个边长为 $b$ 的正方形，然后将剩余部分拼成一个如图 $②$ 所示的长方形．

(1)、上述操作能验证的等式是； $($ 填序号 $)$
$① (a - b)^{2} = a^{2} - 2 a b + b^{2}$ ； $② (a + b) (a - b) = a^{2} - b^{2}$ ； $③ a (a + b)^{2} = a^{3} + 2 a^{2} b + a b^{2}$ ．

(2)、根据(1)中的等式，完成下列各题：
$①$ 已知 $x^{2} - 4 y^{2} = 8$ ， $x + 2 y = 4$ ，求 $x - 2 y$ 的值；

$②$ 计算： $(1 - \frac{1}{2^{2}}) (1 - \frac{1}{3^{2}}) (1 - \frac{1}{4^{2}}) ⋯ (1 - \frac{1}{4 9^{2}}) (1 - \frac{1}{5 0^{2}})$ ．

查看试题解析
20.
附加题：课本中多项式与多项式相乘是利用平面几何图形的面积来表示的，例如：（2a+b）（a+b）=2a²+3ab+b²就可以用图1或图2的面积来表示．

(1)、请写出图3图形的面积表示的代数恒等式；

(2)、试画出一个几何图形，使它的面积能表示（a+b）（a+3b）=a²+4ab+3b² ．

查看试题解析
21.
用四块完全相同的小长方形拼成的一个“回形”正方形．

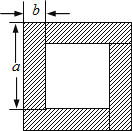(1)、用不同代数式表示图中的阴影部分的面积，你能得到怎样的等式，试用乘法公式说明这个等式成立；

(2)、利用（1）中的结论计算：a+b=2，ab= $\frac{3}{4}$ ，求a﹣b；

(3)、根据（1）中的结论，直接写出x+ $\frac{1}{x}$ 和x﹣ $\frac{1}{x}$ 之间的关系；若x²﹣3x+1=0，分别求出x+ $\frac{1}{x}$ 和（x﹣ $\frac{1}{x}$ ）²的值．

查看试题解析

五、综合题

22. 从边长为 a 的正方形剪掉一个边长为 b 的正方形（如图 1），然后将剩余部分拼成一个长方形（如图 2）．

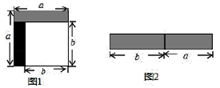(1)、上述操作能验证的等式是_______（请选择正确的一个）

A、a²﹣2ab+b² ＝（a﹣b）² B、a²﹣b²＝（a+b）（a﹣b） C、a² +ab＝a（a+b）

(2)、若 x² ﹣9y²＝12，x+3y＝4，求 x﹣3y 的值；

(3)、计算： $(1 - \frac{1}{2^{2}}) (1 - \frac{1}{3^{2}}) (1 - \frac{1}{4^{2}}) \dots (1 - \frac{1}{2019^{2}}) (1 - \frac{1}{2020^{2}})$ ．

查看试题解析
23. 将完全平方公式作适当变形，可以用来解决很多数学问题．

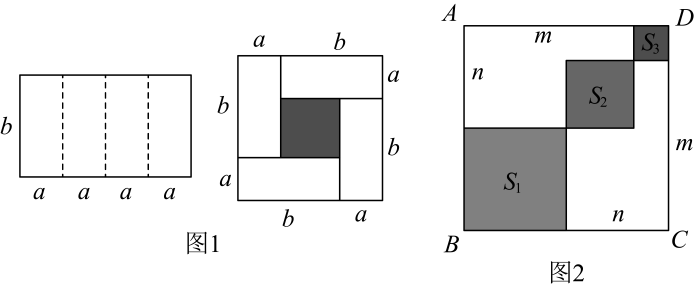(1)、观察图1，写出代数式 ${(a + b)}^{2}$ ， ${(a - b)}^{2}$ ， $a b$ 之间的等量关系：；

(2)、若 $x + y = 6$ ， $x y = 4$ ，则 $x^{2} + y^{2} =$ ； ${(x - y)}^{2} =$ ；

(3)、如图2，边长为5的正方形 $A B C D$ 中放置两个长和宽分别为m ， n（ $m < 5$ ， $n < 5$ ）的长方形，若长方形的周长为12，面积为 $8.5$ ，求图中阴影部分的面积 $S_{1} + S_{2} + S_{3}$ 的值．

查看试题解析