【北师大版·数学】2024年中考二轮复习之平行线的证明
试卷更新日期：2024-04-28 类型：二轮复习
一、选择题
-
1. 如图为商场某品牌椅子的侧面图， ， 与地面平行， ， 则（ ）
A、70° B、65° C、60° D、50°2. 如图，街道与平行，拐角 ， 则拐角 （ ）
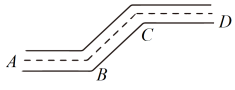A、 B、 C、 D、3. 如图所示，将三角尺的直角顶点放在直尺的一边上， ， ， 则的度数为（ ）
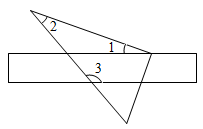A、 B、 C、 D、4. 下列命题中，假命题的是（ ）．A、顺次连接对角线相等的四边形的四边中点所形成的图形是菱形； B、各边对应成比例的两个多边形相似； C、反比例函数的图象既是轴对轴图形，也是中心对称图形； D、已知二次函数 ， 当时，y随x的增大而减小．5. 如图，把一个直角三角尺的直角顶点放在直尺的一边上，则与的关系为（ ）
A、相等 B、 C、互补 D、互余6. 下列命题：①有一个角等于100°的两个等腰三角形相似；②对角线互相垂直的四边形是菱形；③一个角为90°且一组邻边相等的四边形是正方形；④对角线相等的平行四边形是矩形．
其中真命题的个数是（ ）
A、1 B、2 C、3 D、47. 如图， ， ， ACEF，则的度数为（ ）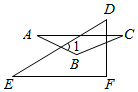
A、 B、 C、 D、8. 如图，AB∥CD，点P为CD上一点，PF是∠EPC的平分线，若∠1=55°，则∠EPD的大小为（ ）
A、60° B、70° C、80° D、100°9. 如图，一块直角三角板60°角的顶点A与直角顶点C分别在两平行线FD，GH上，AB平分∠CAD，交直线GH于点E，则∠ECB的大小为（ ）
A、60° B、45° C、30° D、25°10. 如图，a∥b，一个直角三角形的一个顶点落在其中一条直线上，若∠1=78°，则∠2的度数为（ ）
A、12° B、15° C、25° D、30°二、填空题
-
11. 一副三角板如图摆放，两斜边平行，则°．
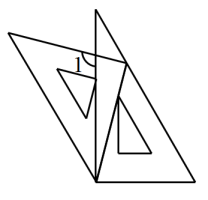12. 如图，直线DE过点A，且DE∥BC.若∠B=60°，∠1=50°，则∠2的度数为.
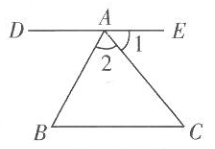13. 如图，已知EF⊥AB，∠1=26°，则当AB∥CD时，∠2=.
14. 如图，直线AB∥CD，∠A=70°，∠C=40°，则∠E=.
15. 如图，AD是△ABC的角平分线，∠C=20°，AB+BD=AC，将△ABD沿AD所在直线翻折，点B在AC边上的落点记为点E，则∠AED的度数为 .
三、解答题
-
16. 如图， ， 点E在线段上，点F在延长线上， ， 求证： ．
17. 如图，∠C=90°，点D是CB的中点，将△ACD沿AD折叠后得到△AED，过点B作BF∥AC交AE的延长线于点F.求证：BF=EF.
18. 如图，点E、F在线段BC上， ， ， ，证明： ．
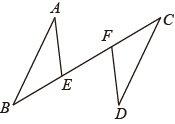19. 如图， ， ， ．求 的度数．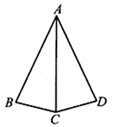
四、综合题
-
20. 如图，在 中， 为 的外角．
(1)、尺规作图：作 的平分线 （保留作图痕迹可加黑，不写作法）；(2)、若 ，在（1）的条件下，求证： ．21. 如图，在△ABC中，∠A＞∠B．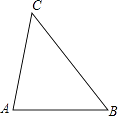
(1)、作边AB的垂直平分线DE，与AB，BC分别相交于点D，E（用尺规作图，保留作图痕迹，不要求写作法）；(2)、在（1）的条件下，连接AE，若∠B=50°，求∠AEC的度数．
