【北师大版·数学】2024年中考二轮复习之数据的分析

试卷更新日期：2024-04-28 类型：二轮复习

进入出卷网下载

一、选择题

1. 一组数据-3，a，2，3，5有唯一的众数3，则这组数据的中位数是（）

A、-2 B、1 C、3 D、5

查看试题解析
2. 学校举行“书香校园”读书活动，某小组的五位同学在这次活动中读书的本数分别为10，11，9，10，12.下列关于这组数据描述正确的是（）

A、众数为10 B、平均数为10 C、方差为2 D、中位数为9

查看试题解析

3. 下表为五种运动耗氧情况，其中耗氧量的中位数是（）.

打网球	跳绳	爬楼梯	慢跑	游泳
$80 L / h$	$90 L / h$	$105 L / h$	$110 L / h$	$115 L / h$

A、

80 L / h

B、

107.5 L / h

C、

105 L / h

D、

110 L / h

查看试题解析

4. 2021年7月24日，杨倩以251.8环的成绩获得2020年东京奥运会射击女子10米气步枪项目金牌，为中国队收获东京奥运会的首枚金牌．她的其中5个成绩（单位：环）分别是：9、8、9、9、10；关于这组数据，以下结论错误的是（）

A、众数为9 B、中位数为9 C、平均数为9 D、方差为2

查看试题解析
5. 下表记录了甲、乙、丙、丁四名射击运动员最近几次选拔赛的成绩（平均数和方差）：
选手
成绩
甲
乙
丙
丁
平均数（环）
$9.4$
$9.5$
$9.4$
$9.5$
方差
$6.3$
$6.8$
$6.7$
$6.6$
根据表中数据，要从中选择一名成绩好且发挥稳定的运动员参加比赛，则选择____较适宜；（）

A、甲 B、乙 C、丙 D、丁

查看试题解析
6. 小明参加校园歌手比赛，唱功得85分，音乐常识得95分，综合知识得90分，学校如果按如图所示的权重计算总评成绩，那么小明的总评成绩是（）

A、87分 B、87.5分 C、88.5分 D、89分

查看试题解析
7. 对于数据：6，3，4，7，6，0，9．下列判断中正确的是（）

A、这组数据的平均数是6，中位数是6 B、这组数据的平均数是6，中位数是7 C、这组数据的平均数是5，中位数是6 D、这组数据的平均数是5，中位数是7

查看试题解析
8. 某校组织“地方文化知识竞赛”，要求每班派一名同学参加.七年级一班组织了三轮预赛，甲、乙、丙、丁四名选手预赛成绩如下表。根据表中数据，该班要选择一名成绩好且发挥稳定的选手参加校级比赛，应选择（）

甲
乙
丙
丁
平均数 $\bar{x}$ （分）
96
93
95
96
方差s²
1.2
0.6
0.6
0.4

A、甲 B、乙 C、丙 D、丁

查看试题解析
9. 秦兵马俑位于秦始皇陵以东1.5千米处的兵马俑坑内，考古人员在确保不会损坏秦兵马俑的情况下，随机测量了10尊秦兵马俑的身高，数据如下（单位：cm）：187，190，193，178，181，181，184，187，187，196，则这10尊秦兵马俑身高的众数为（）

A、181 B、187 C、190 D、193

查看试题解析
10. 养成良好的阅读习惯将受益终身。某文学社团的7名同学在今年2~4月期间阅读课外书籍的数量分别是（单位：本）：10，9，11，5，9，8，7.这组数据的中位数是（）

A、10 B、9 C、8 D、7

查看试题解析

二、填空题

11. 2017年5月28日全国部分宜居城市最高气温的数据如下：
宜居城市
大连
青岛
威海
金华
昆明
三亚
最高气温（℃）
25
28
35
30
26
32
则以上最高气温的中位数为℃.

查看试题解析
12. 数据6，5，7，7，9的众数是　．

查看试题解析
13. “每天一节体育课”成深圳中小学生标配．某校九年级三班随机抽取了 $10$ 名男生进行引体向上测试，他们的成绩（单位：个）如下： $7 ， 11 ， 10 ， 11 ， 6 ， 14 ， 11 ， 10 ， 11 ， 9$ ．则这组数据的中位数为．

查看试题解析
14. 在甲、乙两位射击运动员的10次考核成绩中，两人的考核成绩的平均数相同，方差分别为 $S_{甲}^{2} = 1.45$ ， $S_{乙}^{2} = 0.85$ ，则考核成绩更为稳定的运动员是（填“甲”、“乙”中的一个）

查看试题解析

15. 如表记录了甲、乙、丙三名学生这学期的射击成绩的平均数和方差：

	甲	乙	丙
平均数	9.23	9.3	9.3
方差	0.23	0.017	0.057

根据表中的数据，要选择一名成绩好且发挥稳定的学生参加比赛，应选择．

查看试题解析

三、解答题

16. 对垃圾进行分类投放，能有效提高对垃圾的处理和再利用，减少污染，保护环境．为了了解同学们对垃圾分类知识的了解程度，增强同学们的环保意识，普及垃圾分类及投放的相关知识，某校数学兴趣小组的同学们设计了“垃圾分类知识及投放情况”问卷，并在本校随机抽取若干名同学进行了问卷测试．根据测试成绩分布情况，他们将全部测试成绩分成A、B、C、D四组，绘制了统计图表．
“垃圾分类知识及投放情况”问卷测试成绩统计表
组别
分数/分
频数
A
60＜x≤70
38
B
70＜x≤80
72
C
80＜x≤90
60
D
90＜x≤100
m

依据以上统计信息解答下列问题：

(1)、求得m＝， n＝；

(2)、为了增强大家对垃圾分类的了解，学校组织每个班级学习相关知识，经过一段时间的学习后，再次对原来抽取的这些同学进行问卷测试，发现A组的同学平均成绩提高15分，B组的同学平均成绩提高10分，C组的同学平均成绩提高5分，D组的同学平均成绩没有变化，请估计学习后这些同学的平均成绩提高多少分？若把测试成绩超过85分定为优秀，这些同学再次测试的平均成绩是否达到优秀，为什么？

查看试题解析

四、综合题

17. 小红家到学校有两条公共汽车线路，为了解两条线路的乘车所用时间，小红做了试验，第一周(5个工作日)选择A线路，第二周(5个工作日)选择B线路，每天在固定时间段内乘车2次并分别记录所用时间，数据统计如下：(单位：min)

数据统计表

试验序号	1	2	3	4	5	6	7	8	9	10
A线路所用时间	15	32	15	16	34	18	21	14	35	20
B线路所用时间	25	29	23	25	27	26	31	28	30	24

数据折线统计图

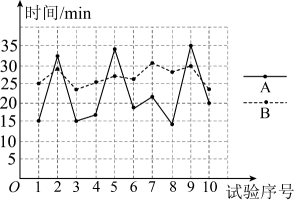
根据以上信息解答下列问题：

	平均数	中位数	众数	方差
A线路所用时间	22	a	15	63.2
B线路所用时间	b	26.5	c	6.36

(1)、填空：

a =

；

b =

；

c =

；

(2)、应用你所学的统计知识，帮助小红分析如何选择乘车线路．

查看试题解析

18. 在一次中学生田径运动会上，根据参加男子跳高初赛的运动员的成绩(单位：m)，绘制出如下的统计图1和统计图2．请根据相关信息，解答下列问题：

(1)、图1中a的值为；

(2)、求统计的这组初赛成绩数据的平均数、众数和中位数；

(3)、根据这组初赛成绩，由高到低确定9人能进入复赛，请直接写出初赛成绩为1.65m的运动员能否进入复赛．

查看试题解析

19. 某公司要招聘一名职员，根据实际需要，从学历、经验、能力和态度四个方面对甲、乙、丙三名应聘者进行了测试，测试的成绩如下表：

项目	应聘者
项目	甲	乙	丙
学历	9	8	8
经验	8	6	9
能力	7	8	8
态度	5	7	5

(1)、如果将学历、经验、能力和态度四项得分按

1 ： 1 ： 1 ： 1

的比例确定每人的最终得分，并以此为依据确定录用者，那么谁将被录用？

(2)、如果你是这家公司的招聘者，请按你认为的各项“重要程度”设计四项得分的比例，说一说你这样设计比例的理由；

(3)、根据你设定的比例，计算甲、乙、丙三名应聘者的得分，从而确定录用者.

查看试题解析

20. “深圳天气”预测未来6天的天气如下：

(1)、“这6天一定下雨”是事件；（选填“必然”“不可能”“随机”）

(2)、这6天最高气温的中位数为；

(3)、这6天最低气温的平均数为．

查看试题解析
21. 近年来，共享单车逐渐成为高校学生喜爱的“绿色出行”方式之一，某高校为了解本校学生出行使用共享单车的情况，随机调查了某天50名出行学生使用共享单车次数的情况，并整理如下统计表．
使用次数
1
2
3
4
5
人数
8
13
11
12
6

(1)、这50名出行学生使用共享单车次数的中位数是，众数是；

(2)、这天中，这50名出行学生平均每人使用共享单车多少次？

查看试题解析
22. 在某次数学测验中，一道题满分3分，老师评分只给整数，即得分只能为0分，1分，2分，3分，汤老师为了了解学生得分情况和试题的难易情况，对初三（1）班所有学生的试题进行了分析整理，并绘制了两幅尚不完整的统计图，如图所示．
小知识：难度系数的计算公式为： $L = \frac{X}{W}$ ，其中 $L$ 为难度系数， $X$ 为样本平均数， $W$ 为试题满分值．《考试说明》指出： $L$ 在0.7以上的题为容易题； $L$ 在 $0.4 ∼ 0.7$ 之间的题为中档题； $L$ 在 $0.2 ∼ 0.4$ 之间的题为较难题．
解答下列问题：

(1)、 $m =$ ▲ ， $n =$ ▲ ，并补全条形统计图；

(2)、在初三（1）班随机抽取一名学生的成绩，求抽中的成绩为2分的概率；

(3)、根据右侧“小知识”，通过计算判断这道题对于该班级来说，属于哪一类难度的试题？

查看试题解析

	甲	乙	丙	丁
平均数 $\bar{x}$ （分）	96	93	95	96
方差s²	1.2	0.6	0.6	0.4

宜居城市	大连	青岛	威海	金华	昆明	三亚
最高气温（℃）	25	28	35	30	26	32

组别	分数/分	频数
A	60＜x≤70	38
B	70＜x≤80	72
C	80＜x≤90	60
D	90＜x≤100	m

使用次数	1	2	3	4	5
人数	8	13	11	12	6