【北师大版·数学】2024年中考二轮复习之一次函数
试卷更新日期:2024-04-28 类型:二轮复习
一、选择题
-
1. 关于函数 , 下列结论正确的是( )A、图象必经过点 B、y随x的增大而增大 C、当时, D、图象经过第一、二、三象限2. 直线y=﹣ax+a与直线y=ax在同一坐标系中的大致图象可能是( )A、
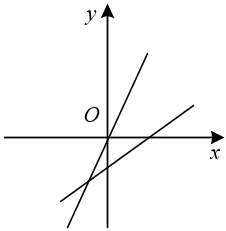 B、
B、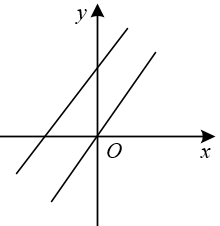 C、
C、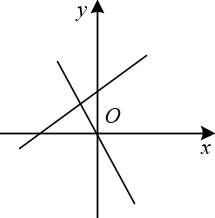 D、
D、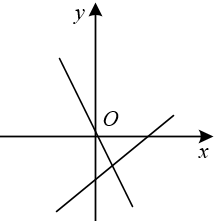 3. 已知一个长方形的周长为 , 相邻两边分别为 , , 则与之间的关系式为( )A、 B、 C、 D、4. 点在正比例函数()的图象上,则k的值为( )A、-15 B、15 C、 D、5. 变量与的关系式是 , 当自变量时,因变量的值是( )A、-5 B、5 C、1 D、-16. 周末小刚骑自行车到外婆家,他从家出发后到达书店,看了一会书,仍按原来的速度继续前行到达外婆家,小刚从家出发到外婆家中,小刚与家的距离随时间变化的函数图象大致如图所示,下列说法正确的是( )
3. 已知一个长方形的周长为 , 相邻两边分别为 , , 则与之间的关系式为( )A、 B、 C、 D、4. 点在正比例函数()的图象上,则k的值为( )A、-15 B、15 C、 D、5. 变量与的关系式是 , 当自变量时,因变量的值是( )A、-5 B、5 C、1 D、-16. 周末小刚骑自行车到外婆家,他从家出发后到达书店,看了一会书,仍按原来的速度继续前行到达外婆家,小刚从家出发到外婆家中,小刚与家的距离随时间变化的函数图象大致如图所示,下列说法正确的是( ) A、小刚从家到书店的骑行速度为5km/h B、小刚在书店停留了1.5h C、书店与外婆家的距离为15km D、小刚从家到外婆家的平均速度为6km/h7. 已知一次函数 , y随着x的增大而减小,则在直角坐标系内它的大致图象是( )A、
A、小刚从家到书店的骑行速度为5km/h B、小刚在书店停留了1.5h C、书店与外婆家的距离为15km D、小刚从家到外婆家的平均速度为6km/h7. 已知一次函数 , y随着x的增大而减小,则在直角坐标系内它的大致图象是( )A、 B、
B、 C、
C、 D、
D、 8. 如图,直线 与 交于点 , 有四个结论:① ;② ;③当 时,;④当 时, , 其中正确的是 ( )
8. 如图,直线 与 交于点 , 有四个结论:① ;② ;③当 时,;④当 时, , 其中正确的是 ( ) A、①② B、①③ C、①④ D、②④9. 正方形的周长y是边长x的函数,则下列表示正方形周长y与边长x之间的函数关系正确的是( )A、 B、 C、 D、10. 已知 , , 则一次函数的图象可能是( )A、
A、①② B、①③ C、①④ D、②④9. 正方形的周长y是边长x的函数,则下列表示正方形周长y与边长x之间的函数关系正确的是( )A、 B、 C、 D、10. 已知 , , 则一次函数的图象可能是( )A、 B、
B、 C、
C、 D、
D、
二、填空题
-
11. 已知 是一次函数,则m=.12. 在函数中,自变量的取值范围是 .13. 在一次函数 中,的值随着 值得增大而增大,请你写出一个符合条件的一次函数解析式 .14. 一次函数的图象经过原点,则y随x的增大而 .(填“增大”或“减小”)15. 函数y=的自变量x的取值范围是.
三、解答题
-
16. 已知一次函数的图象过M(1,3),N(-2,12)两点.(1)、求函数的解析式;(2)、试判断点P(-2,-6)是否在函数的图象上,并说明理由.17. 甲开汽车,乙骑自行车从M地出发沿一条公路匀速前往N地,乙先出发一段时间后甲才出发,设乙行驶的时间为t(h),甲乙两人之间的距离为y(km),y与t的函数关系如图1所示,其中点C的坐标为( , ),请解决以下问题:
(1)甲比乙晚出发几小时?
(2)分别求出甲、乙二人的速度;
(3)丙骑摩托车与乙同时出发,从N地沿同一条公路匀速前往M地,若丙经过h与乙相遇.
①设丙与M地的距离为S(km),行驶的时间为t(h),求S与t之间的函数关系式(不用写自变量的取值范围)
②丙与乙相遇后再用多少时间与甲相遇.
 18. 一次函数y=kx+b的图象经过点(2,﹣1)和(0,3),求这个一次函数的解析式.
18. 一次函数y=kx+b的图象经过点(2,﹣1)和(0,3),求这个一次函数的解析式.四、综合题
-
19. 如图1,直线交x轴于点A,交y轴于点B,点C在上,且 .
 (1)、直接写出点C的坐标为;(2)、P为x轴负半轴上一点,且 , 连接 , 设的面积为S,直接写出S与m的函数关系式;(3)、在(2)的条件下,过点B作 , 交x轴于点D,若 , 求点D的坐标.20. 如图,在平面直角坐标系中,轴,轴, , 点B的坐标为 . 将沿AC折叠得到 , 点B落在点D的位置,交y轴于点E,
(1)、直接写出点C的坐标为;(2)、P为x轴负半轴上一点,且 , 连接 , 设的面积为S,直接写出S与m的函数关系式;(3)、在(2)的条件下,过点B作 , 交x轴于点D,若 , 求点D的坐标.20. 如图,在平面直角坐标系中,轴,轴, , 点B的坐标为 . 将沿AC折叠得到 , 点B落在点D的位置,交y轴于点E, (1)、求点D的坐标.(2)、求经过点A、D的直线的解析式.21. 物理实验证实:在弹性限度内,某弹簧长度y( )与所挂物体质量x( )满足函数关系 .下表是测量物体质量时,该弹簧长度与所挂物体质量的数量关系.
(1)、求点D的坐标.(2)、求经过点A、D的直线的解析式.21. 物理实验证实:在弹性限度内,某弹簧长度y( )与所挂物体质量x( )满足函数关系 .下表是测量物体质量时,该弹簧长度与所挂物体质量的数量关系.x
0
2
5
y
15
19
25
(1)、求y与x的函数关系式;(2)、当弹簧长度为20 时,求所挂物体的质量.22. 粤港澳大湾区自动驾驶产业联盟积极推进自动驾驶出租车应用落地工作,无人化是自动驾驶的终极目标.某公交集团拟在今明两年共投资9000万元改装260辆无人驾驶出租车投放市场.今年每辆无人驾驶出租车的改装费用是50万元,预计明年每辆无人驾驶出租车的改装费用可下降 .(1)、求明年每辆无人驾驶出租车的预计改装费用是多少万元;(2)、求明年改装的无人驾驶出租车是多少辆.