2024年中考数学热点探究二十二 学科融合
试卷更新日期:2024-04-27 类型:二轮复习
一、选择题
-
1. 生物学指出,在生物链中大约只有的能量能够流动到下一个营养级,在这条生物链中(表示第个营养级,),要使获得785千焦的能量,那么需要提供的能量约为(用科学记数法表示)( ).A、千焦 B、千焦 C、千焦 D、千焦2. 在下列化学元素符号中,既是轴对称图形又是中心对称图形的是( )A、H B、N C、S D、F3. 下面四种化学仪器的示意图是轴对称图形的是( )A、
 B、
B、 C、
C、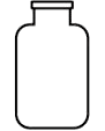 D、
D、 4. 生物兴趣小组探究酒精对某种鱼类的心率是否有影响,实验得出心率与酒精浓度的关系如图所示,下列说法正确的是( )
4. 生物兴趣小组探究酒精对某种鱼类的心率是否有影响,实验得出心率与酒精浓度的关系如图所示,下列说法正确的是( ) A、酒精浓度越大,心率越高 B、酒精对这种鱼类的心率没有影响 C、当酒精浓度是时,心率是168次/分 D、心率与酒精浓度是反比例函数关系5. 在物理实验课上,小明用弹簧称将铁块A悬于盛有水的水槽中(如图),然后匀速向上提起,直至铁块完全露出水面一定高度,则能反映弹簧秤的读数y(单位:N)与铁块被提起的高度x(单位:cm)之间的函数关系的图象大致是( )
A、酒精浓度越大,心率越高 B、酒精对这种鱼类的心率没有影响 C、当酒精浓度是时,心率是168次/分 D、心率与酒精浓度是反比例函数关系5. 在物理实验课上,小明用弹簧称将铁块A悬于盛有水的水槽中(如图),然后匀速向上提起,直至铁块完全露出水面一定高度,则能反映弹簧秤的读数y(单位:N)与铁块被提起的高度x(单位:cm)之间的函数关系的图象大致是( )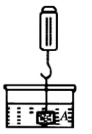 A、
A、 B、
B、 C、
C、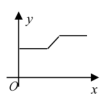 D、
D、 6. 如图,一束平行于主光轴的光线经凸透镜折射后,其折射光线与一束经过光心的光线相交于点 , 点为焦点.若 , 则的度数为( )
6. 如图,一束平行于主光轴的光线经凸透镜折射后,其折射光线与一束经过光心的光线相交于点 , 点为焦点.若 , 则的度数为( )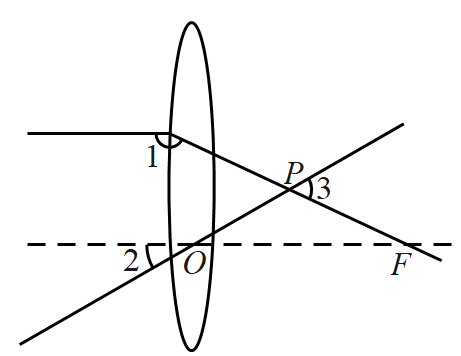 A、 B、 C、 D、7. 光线在不同介质中的传播速度是不同的,因此当光线从水中射向空气时,要发生折射,由于折射率相同,所以在水中平行的光线,在空气中也是平行的.如图,的度数为( )
A、 B、 C、 D、7. 光线在不同介质中的传播速度是不同的,因此当光线从水中射向空气时,要发生折射,由于折射率相同,所以在水中平行的光线,在空气中也是平行的.如图,的度数为( )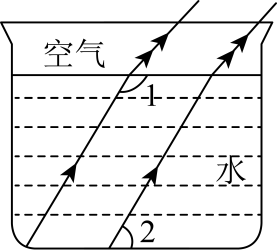 A、 B、 C、 D、8. 数学是研究化学的重要工具,数学知识广泛应用于化学邻域,比如在学习化学的醇类化学式中,甲醇化学式为 , 乙醇化学式为 , 丙醇化学式为 , 设碳原子的数目为为正整数 , 则醇类的化学式可以用下列哪个式子来表示( )A、 B、 C、 D、9. 小明用地理中所学的等高线的知识在某地进行野外考察,他根据当地地形画出了“等高线示意图”,如图所示若三点均在相应的等高线上,且三点在同一直线上,则的值为( )
A、 B、 C、 D、8. 数学是研究化学的重要工具,数学知识广泛应用于化学邻域,比如在学习化学的醇类化学式中,甲醇化学式为 , 乙醇化学式为 , 丙醇化学式为 , 设碳原子的数目为为正整数 , 则醇类的化学式可以用下列哪个式子来表示( )A、 B、 C、 D、9. 小明用地理中所学的等高线的知识在某地进行野外考察,他根据当地地形画出了“等高线示意图”,如图所示若三点均在相应的等高线上,且三点在同一直线上,则的值为( ) A、 B、 C、 D、2
A、 B、 C、 D、2二、填空题
-
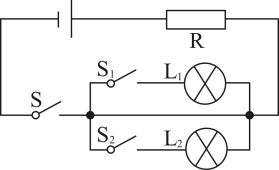
10. 在物理实验课上,同学们用三个开关、两个灯泡、一个电源、一个电阻及若干条导线连接如图所示的电路图,随机闭合图中的两个开关,有一个灯泡发光的概率是.
 11. 生物的遗传信息大多储存在分子上,一个分子直径为 , 用科学记数法可表示为.12. 生物学家研究发现,人体许多特征都是由基因决定的.如人的单双眼皮由常染色体上的一对基因决定,决定双眼皮的基因是显性的,单眼皮的基因是隐性的,因此决定单双眼皮的一对基因有三种,其中基因为和的人双眼皮,基因为的人单眼皮,父母分别将他们一对基因中的一个基因等可能地遗传给子女.若父亲的基因是 , 母亲的基因是 , 则他们的子女为双眼皮的概率为 .13. 烷烃是一类由碳、氢元素组成的有机化合物,在生产生活中可作为燃料、润滑剂等原料,也可用于动、植物的养护.通常用碳原子的个数命名为甲烷、乙烷、丙烷、......、癸烷(当碳原子数目超过10个时即用汉文数字表示,如十一烷、十二烷……)等,甲烷的化学式为 , 乙烷的化学式为 , 丙烷的化学式为 , 其分子结构模型如图所示,按照此规律,十二烷的化学式为.
11. 生物的遗传信息大多储存在分子上,一个分子直径为 , 用科学记数法可表示为.12. 生物学家研究发现,人体许多特征都是由基因决定的.如人的单双眼皮由常染色体上的一对基因决定,决定双眼皮的基因是显性的,单眼皮的基因是隐性的,因此决定单双眼皮的一对基因有三种,其中基因为和的人双眼皮,基因为的人单眼皮,父母分别将他们一对基因中的一个基因等可能地遗传给子女.若父亲的基因是 , 母亲的基因是 , 则他们的子女为双眼皮的概率为 .13. 烷烃是一类由碳、氢元素组成的有机化合物,在生产生活中可作为燃料、润滑剂等原料,也可用于动、植物的养护.通常用碳原子的个数命名为甲烷、乙烷、丙烷、......、癸烷(当碳原子数目超过10个时即用汉文数字表示,如十一烷、十二烷……)等,甲烷的化学式为 , 乙烷的化学式为 , 丙烷的化学式为 , 其分子结构模型如图所示,按照此规律,十二烷的化学式为. 14. “数学是将科学现象升华到科学本质认识的重要工具”,比如在化学中,乙烯的化学式是 , 丙稀的化学式是…,碳原子和氢原子的数目满足一定数学规律.设碳原子的数目为n(n为正整数,且n≥2),则这类稀的化学式可用式子来表示.15. “数学是将科学现象升华到科学本质认识的重要工具”,比如在化学中,甲烷的化学式是 , 乙烷的化学式是 , 丙烷的化学式是 , 设碳原子的数目为为正整数n(n为正整数),则它们的化学式都可用式子来表示.16. 化学课上,小红学到了这样一个知识:将二氧化碳通入澄清石灰水,澄清石灰水会变浑浊.以下为常考的四个实验: . 高锰酸钾制取氧气, . 电解水, . 木炭还原氧化铜, . 一氧化碳还原氧化铜,已知这四个实验中, , 两个实验均能产生二氧化碳,若小华从四个实验中任意选做两个,则两个实验所产生的气体均能使澄清石灰水变浑浊的概率为 .
14. “数学是将科学现象升华到科学本质认识的重要工具”,比如在化学中,乙烯的化学式是 , 丙稀的化学式是…,碳原子和氢原子的数目满足一定数学规律.设碳原子的数目为n(n为正整数,且n≥2),则这类稀的化学式可用式子来表示.15. “数学是将科学现象升华到科学本质认识的重要工具”,比如在化学中,甲烷的化学式是 , 乙烷的化学式是 , 丙烷的化学式是 , 设碳原子的数目为为正整数n(n为正整数),则它们的化学式都可用式子来表示.16. 化学课上,小红学到了这样一个知识:将二氧化碳通入澄清石灰水,澄清石灰水会变浑浊.以下为常考的四个实验: . 高锰酸钾制取氧气, . 电解水, . 木炭还原氧化铜, . 一氧化碳还原氧化铜,已知这四个实验中, , 两个实验均能产生二氧化碳,若小华从四个实验中任意选做两个,则两个实验所产生的气体均能使澄清石灰水变浑浊的概率为 .三、解答题
-
17. 根据物理学知识,在压力不变的情况下,某物体承受的压强是它的受力面积的反比例函数,其函数图象如图所示.
 (1)、关于的函数关系式为 .(2)、求当时,物体所受的压强是 .(3)、当时,求受力面积的变化范围.18. 如图1,某人的一器官后面A处长了一个新生物,现需检测其到皮肤的距离(图1).为避免伤害器官,可利用一种新型检测技术,检测射线可避开器官从侧面测量.某医疗小组制定方案,通过医疗仪器的测量获得相关数据,并利用数据计算出新生物到皮肤的距离方案如下:
(1)、关于的函数关系式为 .(2)、求当时,物体所受的压强是 .(3)、当时,求受力面积的变化范围.18. 如图1,某人的一器官后面A处长了一个新生物,现需检测其到皮肤的距离(图1).为避免伤害器官,可利用一种新型检测技术,检测射线可避开器官从侧面测量.某医疗小组制定方案,通过医疗仪器的测量获得相关数据,并利用数据计算出新生物到皮肤的距离方案如下:课题
检测新生物到皮肤的距离
工具
医疗仪器等
示意图


说明
如图2,新生物在A处,先在皮肤上选择最大限度地避开器官的B处照射新生物,检测射线与皮肤MN的夹角为∠DBN;再在皮肤上选择距离B处9cm的C处照射新生物,检测射线与皮肤MN的夹角为∠ECN.
测量数据
∠DBN=35°,∠ECN=22°,BC=9cm
请你根据上表中的测量数据,计算新生物A处到皮肤的距离.(结果精确到0.1cm)
(参考数据:sin35°≈0.57,cos35°≈0.82,tan35°≈0.70,sin22°≈0.37,cos22°≈0.93,tan22°≈0.40)
19. 在某次化学实验中,晓欢在实验桌上放置了1杯纯净水,1杯生理盐水,2杯白糖水,共4杯液体.装这些液体的烧杯相同且液体体积也相同(外观均相同),由于没有贴标签,所以最终晓欢也无法分辨烧杯中的液体具体是哪种.现在晓欢要对这些液体进行甄别. (1)、求从这4杯液体中任取1杯是生理盐水的概率;(2)、晓欢从这4杯液体中同时任取2杯,请用画树状图或列表法求晓欢取出的2杯均是白糖水的概率.
(1)、求从这4杯液体中任取1杯是生理盐水的概率;(2)、晓欢从这4杯液体中同时任取2杯,请用画树状图或列表法求晓欢取出的2杯均是白糖水的概率.四、实践探究题
-
20. 阅读与思考
下面是小宇同学的一篇日记,请仔细阅读并完成相应的任务.
在物理活动课上,我们“博学”小组的同学,参加了一次“探究电功率与电阻之间的函数关系”的活动.
第一步,实验测量.根据物理知识,改变电阻的大小,通过测量电路中的电流,计算电功率.

第二步,整理数据.
R/Ω … 3 6 9 12 15 … P/W … 3 1.5 1 0.75 0.7 … 第三步,描点连线,以的数值为横坐标,对应的数值为纵坐标在平面直角坐标系中描出以表中数值为坐标的各点,并用光滑的曲线顺次连接这些点.
在数据分析时,我发现一个数据有错误,重新测量计算后,证明了我的猜想正确,并修改了表中这个数据.实验结束后,大家都有很多收获,每人都撰写了日记.
任务:
(1)、表格中错误的数据是 , 与的函数表达式为;(2)、在平面直角坐标系中,画出与的函数图象; (3)、结合图象,直接写出P大于6W时R的取值范围.21. 学科综合
(3)、结合图象,直接写出P大于6W时R的取值范围.21. 学科综合我们在物理学科中学过:光线从空气射入水中会发生折射现象如图 , 我们把称为折射率其中代表入射角,代表折射角 .
观察实验
为了观察光线的折射现象,设计了图所示的实验,即通过细管可以看见水底的物块 , 但不在细管所在直线上,图是实验的示意图,四边形为矩形,点 , , 在同一直线上,测得 , .
 (1)、求入射角的度数.(2)、若 , 求光线从空气射入水中的折射率参考数据: , ,22. 【综合与实践】
(1)、求入射角的度数.(2)、若 , 求光线从空气射入水中的折射率参考数据: , ,22. 【综合与实践】有言道:“杆秤一头称起人间生计,一头称起天地良心”.某兴趣小组将利用物理学中杠杆原理制作简易杆秤.小组先设计方案,然后动手制作,再结合实际进行调试,请完成下列方案设计中的任务.
【知识背景】如图,称重物时,移动秤砣可使杆秤平衡,根据杠杆原理推导得:.其中秤盘质量克,重物质量克,秤砣质量克,秤纽与秤盘的水平距离为厘米,科纽与零刻线的水平距离为厘米,秤砣与零刻线的水平距离为厘米.
【方案设计】
目标:设计简易杆秤.设定 , 最大可称重物质量为1000克,零刻线与末刻线的距离定为50厘米.
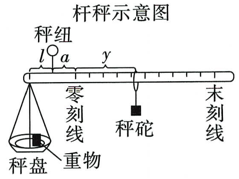 (1)、当秤盘不放重物,秤砣在零刻线时,杆秤平衡,请列出关于l,a的方程;(2)、当秤盘放入质量为1000克的重物,秤砣从零刻度线移至末刻线时,杠杆平衡,请列出关于l,a的方程;(3)、根据(1)和(2)所列方程,求出l和的值;(4)、根据(1)-(3),求关于的函数解析式;(5)、从零刻线开始,每隔100克在科杆上找到对应刻线,请写出相邻刻线间的距离.23. 如图,甲、乙分别从A(-9,0),B(13,0)两点同时出发,甲朝着正北方向,以每秒3个单位长度的速度运动;乙朝着正西方向,以每秒4个单位长度的速度运动.设运动时间为t秒.
(1)、当秤盘不放重物,秤砣在零刻线时,杆秤平衡,请列出关于l,a的方程;(2)、当秤盘放入质量为1000克的重物,秤砣从零刻度线移至末刻线时,杠杆平衡,请列出关于l,a的方程;(3)、根据(1)和(2)所列方程,求出l和的值;(4)、根据(1)-(3),求关于的函数解析式;(5)、从零刻线开始,每隔100克在科杆上找到对应刻线,请写出相邻刻线间的距离.23. 如图,甲、乙分别从A(-9,0),B(13,0)两点同时出发,甲朝着正北方向,以每秒3个单位长度的速度运动;乙朝着正西方向,以每秒4个单位长度的速度运动.设运动时间为t秒.规定:t秒时,甲到达的位置记为点A,乙到达的位置记为点B,例如,1秒时,甲到达的位置记为A,乙到达的位置记为B,(如图所示);2.5秒时,甲到达的位置记为A2.5等等.容易知道,两条平行且相等的线段,其中包含有相同的方位信息所以,在研究有关运动问题时,为研究方便,我们可把点或线段进行合适的平移后,再去研究(物理上的相对运动观,就是源于这种数学方法)现对t秒时,甲、乙到达的位置点At , Bt , 按如下步骤操作:
第一步:连接AtBt;
第二步:把线段AtBt进行平移,使点Bt与点B重合,平移后,点A1的对应点用点At’标记
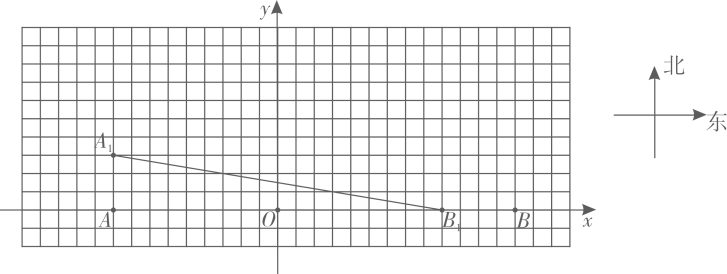
解答下列问题:
(1)、[理解与初步应用]
当t=1时,①利用网格,在上图中画出A1 , B1经过上述第二步操作后的图形;
②此时,甲在乙的什么方位?(请填空)
答:此时,甲在乙的北偏西θ°(其中tanθ°= , 两者相距 个单位长度.
(2)、[实验与数据整理]
补全下表:t的取值
1
2
3
t
点At'的坐标
(-5,3)
( , )
( , )
( , )
(3)、[数据分析与结论运用]①如果把点At'的横、纵坐标分别用变量x,y表示,则y与x之间的函数关系式为;
②点A3.5’的坐标为
(4)、[拓展应用]
我们知道,在运动过程中的任意时刻t,甲相对于乙的方位(即,点At相对于点Bt的方位)与At'相对于点B的方位相同.这为我们解决某些问题,提供了新思路.请解答:运动过程中,甲、乙之间的最近距离为个单位长度.
24. 生物学上通常用“标记重捕法”来估算特定区域内某种群的数量.如在固定区域内用捕虫网捕捉了40只田鼠,将它们标记后放回直到充分混合后,用同一个捕虫网捕捉了80只田鼠,其中有16只是被标记的,于是估算该区域田鼠的数量为:(只).
某研究小组考察了一湖泊中的某鱼种群的年龄组成,结果如下表,请回答问题:
年龄
A
B
C
D
……
个体数量
92
187
x
y
……
注:表中“”表示鱼的年龄年,表示年龄年,表示年龄年,表示年龄为年.
(1)、年龄为 , , 的个体数量的平均数为125,年龄在 , , , 的个体数量的中位数是95,则 , (其中).(2)、若将年龄为的鱼全部标记后并放回湖泊,充分混合后,捕捉120条鱼,其中被标记鱼有12条,那么该湖泊里一共约有多少条鱼?(3)、现捕获A,B,C,D年龄段的鱼各一条,从中任抓两条,请用列表或画树状图求抓到的是和年龄的鱼的概率.25. 为研究某种化学试剂的挥发情况,某研究团队在两种不同的场景下做对比实验,收集了该试剂挥发过程中剩余质量克随时间分钟变化的数据 , 并分别绘制在直角坐标系中,如图所示.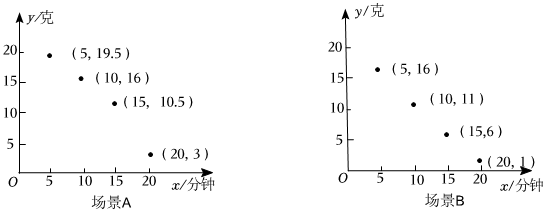 (1)、从 , , 中,选择适当的函数模型分别模拟两种场景下随变化的函数关系,并求出相应的函数表达式;(2)、查阅文献可知,该化学试剂发挥作用的最低质量为克在上述实验中,该化学试剂在哪种场景下发挥作用的时间更长?26. 化学课上,小红学到:将二氧化碳气体通入澄清石灰水,澄清石灰水就会变浑浊以下为四个常考的实验:
(1)、从 , , 中,选择适当的函数模型分别模拟两种场景下随变化的函数关系,并求出相应的函数表达式;(2)、查阅文献可知,该化学试剂发挥作用的最低质量为克在上述实验中,该化学试剂在哪种场景下发挥作用的时间更长?26. 化学课上,小红学到:将二氧化碳气体通入澄清石灰水,澄清石灰水就会变浑浊以下为四个常考的实验:A.高锰酸钾制取氧气:
B.碳酸钙制取二氧化碳:
C.电解水:
D.一氧化碳还原每化
(1)、若小红从四个实验中任意选一个实验,实验产生的气体不会使澄清石灰水变浑浊的概率是多少?(2)、若小红从四个实验中任意选两个实验,请用列表或树状图的方法求两个实验产生的气体均能使澄清石灰水变浑浊的概率.27. 请阅读以下材料,并完成相应的任务【阅读材料】在《阿基米德全集》中的《引理集》中记述了伟大的古希腊数学家、哲学家、物理学家阿基米德提出的六个有关圆的引理,其中第二个引理是:
如图1,点P是弧的任意一点,于点C,点D在弦上且 , 在弧上取一点Q,使弧=弧 , 连接 , 则有.
 (1)、如图2,小明同学尝试说明“”,于是他连接了 , , , , 请根据小明的思路完成后续证明过程;(2)、如图3,以为直径的半圆上有一点P, , 直线l与相切于点P,过点于点E,交于点Q,求出的长.
(1)、如图2,小明同学尝试说明“”,于是他连接了 , , , , 请根据小明的思路完成后续证明过程;(2)、如图3,以为直径的半圆上有一点P, , 直线l与相切于点P,过点于点E,交于点Q,求出的长.