2024年中考数学热点探究二十 PISA测试题
试卷更新日期:2024-04-27 类型:二轮复习
一、选择题
-
1. 近几年,二维码逐渐进入了人们的生活,成为广大民众生活中不可或缺的一部分,小刚将二维码打印在面积为20的正方形纸片上,如图,为了估计黑色阴影部分的面积,他在纸内随机掷点,经过大量重复实验,发现点落在黑色阴影的频率稳定在左右,则据此估计此二维码中黑色阴影的面积为( )
 A、8 B、12 C、 D、2. 生物学指出,在生物链中大约只有的能量能够流动到下一个营养级,在这条生物链中(表示第个营养级,),要使获得785千焦的能量,那么需要提供的能量约为(用科学记数法表示)( ).A、千焦 B、千焦 C、千焦 D、千焦3. 二进制是计算技术中广泛采用的一种数制,由18世纪德国数理哲学大师菜布尼兹发现,二进制数据是用0和1两个数码来表示的数,如01,10分别表示不同的二进制数,在有一个0,两个1组成的二进制数中,两个1相邻的概率是( )A、 B、 C、 D、4. 小明不慎把家里的圆形镜子打碎了,其中三块碎片如图所示,三块碎片中最有可能配到与原来一样大小的圆形镜子的碎片是( )
A、8 B、12 C、 D、2. 生物学指出,在生物链中大约只有的能量能够流动到下一个营养级,在这条生物链中(表示第个营养级,),要使获得785千焦的能量,那么需要提供的能量约为(用科学记数法表示)( ).A、千焦 B、千焦 C、千焦 D、千焦3. 二进制是计算技术中广泛采用的一种数制,由18世纪德国数理哲学大师菜布尼兹发现,二进制数据是用0和1两个数码来表示的数,如01,10分别表示不同的二进制数,在有一个0,两个1组成的二进制数中,两个1相邻的概率是( )A、 B、 C、 D、4. 小明不慎把家里的圆形镜子打碎了,其中三块碎片如图所示,三块碎片中最有可能配到与原来一样大小的圆形镜子的碎片是( ) A、① B、② C、③ D、均不可能5. 二维码是一种编码方式,它是用某种特定的几何图形按一定规律在平面(二维方向上)分布,采用黑白相间的图形记录数据符号信息的.某社区为方便管理,仿照二维码编码的方式为居民设计了一个身份识别图案系统:在 的正方形网格中,白色正方形表示数字0,黑色正方形表示数字1,将第i行第j列表示的数记为 (其中i,j都是不大于4的正整数),例如,图中, .对第i行使用公式 进行计算,所得结果 , , , 分别表示居民楼号,单元号,楼层和房间号.例如,图中, , ,说明该居民住在9层,2号房间,即902号.有下面结论:① ;②图中代表的居民居住在11号楼;③ ,其中正确的是( )
A、① B、② C、③ D、均不可能5. 二维码是一种编码方式,它是用某种特定的几何图形按一定规律在平面(二维方向上)分布,采用黑白相间的图形记录数据符号信息的.某社区为方便管理,仿照二维码编码的方式为居民设计了一个身份识别图案系统:在 的正方形网格中,白色正方形表示数字0,黑色正方形表示数字1,将第i行第j列表示的数记为 (其中i,j都是不大于4的正整数),例如,图中, .对第i行使用公式 进行计算,所得结果 , , , 分别表示居民楼号,单元号,楼层和房间号.例如,图中, , ,说明该居民住在9层,2号房间,即902号.有下面结论:① ;②图中代表的居民居住在11号楼;③ ,其中正确的是( ) A、③ B、①② C、①③ D、①②③6. 某社区为了打造“书香社区”,丰富小区居民的业余文化生活,计划出资500元全部用于采购A,B,C三种图书,A种每本30元,B种每本25元,C种每本20元,其中A种图书至少买5本,最多买6本(三种图书都要买),此次采购的方案有( )A、5种 B、6种 C、7种 D、8种7. 某娱乐设施每次能够容纳4人一组进场游玩,甲、乙、丙、丁排队等候,甲前面有若干人,乙排在甲后面,中间隔着2人,丙排在乙后面,中间隔着1人,丁排在丙后面,中间隔着1人,丁后面也有若干人.下列说法:①如果甲和乙同一组,那么丙和丁也同一组;②如果甲和乙不同一组,那么丙和丁也不同一组;③如果丙和丁同一组,那么甲和乙也同一组;④如果丙和丁不同一组,那么甲和乙也不同一组.正确的个数为( )A、1 B、2 C、3 D、48. 问题:如图 , 矩形纸片中, , , 要求将矩形纸片剪两刀后不重叠、无缝隙地拼接成一个正方形.甲、乙两位同学根据剪拼前后面积不变,确定了正方形的边长为 , 并分别设计了如下的方案.
A、③ B、①② C、①③ D、①②③6. 某社区为了打造“书香社区”,丰富小区居民的业余文化生活,计划出资500元全部用于采购A,B,C三种图书,A种每本30元,B种每本25元,C种每本20元,其中A种图书至少买5本,最多买6本(三种图书都要买),此次采购的方案有( )A、5种 B、6种 C、7种 D、8种7. 某娱乐设施每次能够容纳4人一组进场游玩,甲、乙、丙、丁排队等候,甲前面有若干人,乙排在甲后面,中间隔着2人,丙排在乙后面,中间隔着1人,丁排在丙后面,中间隔着1人,丁后面也有若干人.下列说法:①如果甲和乙同一组,那么丙和丁也同一组;②如果甲和乙不同一组,那么丙和丁也不同一组;③如果丙和丁同一组,那么甲和乙也同一组;④如果丙和丁不同一组,那么甲和乙也不同一组.正确的个数为( )A、1 B、2 C、3 D、48. 问题:如图 , 矩形纸片中, , , 要求将矩形纸片剪两刀后不重叠、无缝隙地拼接成一个正方形.甲、乙两位同学根据剪拼前后面积不变,确定了正方形的边长为 , 并分别设计了如下的方案.甲:如图 , 在上找点E,连接 , 使 , 作 , 交于F点,完成分割;
乙:如图 , 在上找点F,连接 , 使 , 以为直径作圆,交于点E,连接即可完成分割.下列结论正确的是( )
 A、甲、乙的分割都错误 B、甲、乙的分割都正确 C、乙的分割正确,图3中 D、甲的分割正确,图2中9. 同型号的甲、乙两辆车加满气体燃料后均可行驶210km,它们各自单独行驶并返回的最远距离是105km,现在它们都从A地出发,行驶途中停下来从甲车的气体燃料桶抽一些气体燃料注入乙车的气体燃料桶,然后甲车再行驶返回A地,而乙车继续行驶,到B地后再行驶返回A地.则B地最远可距离A地( )A、120km B、140km C、160km D、180km10. 小红用次数最少的对折方法验证了一条四边形丝巾的形状是正方形,她对折了( )A、1次 B、2次 C、3次 D、4次11. 如图的电子装置中,红黑两枚跳棋开始放置在边长为2的正六边形 的顶点A处.两枚跳棋跳动规则是:红跳棋按顺时针方向1秒钟跳1个顶点,黑跳棋按逆时针方向3秒钟跳1个顶点,两枚跳棋同时跳动,经过2022秒钟后,两枚跳棋之间的距离是( )
A、甲、乙的分割都错误 B、甲、乙的分割都正确 C、乙的分割正确,图3中 D、甲的分割正确,图2中9. 同型号的甲、乙两辆车加满气体燃料后均可行驶210km,它们各自单独行驶并返回的最远距离是105km,现在它们都从A地出发,行驶途中停下来从甲车的气体燃料桶抽一些气体燃料注入乙车的气体燃料桶,然后甲车再行驶返回A地,而乙车继续行驶,到B地后再行驶返回A地.则B地最远可距离A地( )A、120km B、140km C、160km D、180km10. 小红用次数最少的对折方法验证了一条四边形丝巾的形状是正方形,她对折了( )A、1次 B、2次 C、3次 D、4次11. 如图的电子装置中,红黑两枚跳棋开始放置在边长为2的正六边形 的顶点A处.两枚跳棋跳动规则是:红跳棋按顺时针方向1秒钟跳1个顶点,黑跳棋按逆时针方向3秒钟跳1个顶点,两枚跳棋同时跳动,经过2022秒钟后,两枚跳棋之间的距离是( )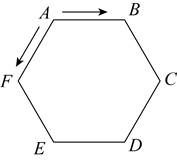 A、4 B、 C、2 D、0
A、4 B、 C、2 D、0二、填空题
-
12. 远古时期,人们通过在绳子上打结来记录数量,即“结绳计数”,类似现在我们熟悉的“进位制”.如图所示是一位母亲记录孩子出生后的天数,在从右向左依次排列的不同绳子上打结,满五进一,根据图示可知,孩子已经出生的天数是天.
 13. 当今大数据时代,“二维码”具有存储量大.保密性强、追踪性高等特点,它己被广泛应用于我们的日常生活中,尤其在全球“新冠”疫情防控期间,区区“二维码”已经展现出无穷威力.看似“码码相同”,实则“码码不同”.通常,一个“二维码”由1000个大大小小的黑白小方格组成,其中小方格专门用做纠错码和其他用途的编码,这相当于1000个方格只有200个方格作为数据码.根据相关数学知识,这200个方格可以生成个不同的数据二维码,现有四名网友对的理解如下:
13. 当今大数据时代,“二维码”具有存储量大.保密性强、追踪性高等特点,它己被广泛应用于我们的日常生活中,尤其在全球“新冠”疫情防控期间,区区“二维码”已经展现出无穷威力.看似“码码相同”,实则“码码不同”.通常,一个“二维码”由1000个大大小小的黑白小方格组成,其中小方格专门用做纠错码和其他用途的编码,这相当于1000个方格只有200个方格作为数据码.根据相关数学知识,这200个方格可以生成个不同的数据二维码,现有四名网友对的理解如下:YYDS(永远的神):就是200个2相乘,它是一个非常非常大的数;
DDDD(懂的都懂):等于;
JXND(觉醒年代):的个位数字是6;
QGYW(强国有我):我知道 , 所以我估计比大.
其中对的理解错误的网友是(填写网名字母代号).
14. 为参加“重庆长江三峡国际马拉松”比赛,甲乙两运动员相约晨练跑步.甲比乙早1分钟跑步出门,3分钟后他们相遇.两人寒暄2分钟后,决定进行同向跑步练习,练习时甲的速度是180米/分,乙的速度是240米/分.练习5分钟后,乙突感身体不适,于是他按原路以出门时的速度返回,直到与甲再次相遇.如图是甲、乙之间的距离 (千米)与甲跑步所用时间 (分钟)之间的函数图象.问甲从他家出发到他们再次相遇时,一共用了分钟. 15.
15.如图,有一颗棋子放在图中的1号位置上,现按顺时针方向,第一次跳一步到2号位置上第二次跳两步跳到4号位置上,第三次跳三步又跳到了1号位置上,第四次跳四步…一直进行下去,那么第2017次跳2017步就跳到了号位置上.
 16. 为了从2018枚外形相同的金蛋中找出唯一的有奖金蛋,检查员将这些金蛋按1﹣2018的顺序进行标号.第一次先取出编号为单数的金蛋,发现其中没有有奖金蛋,他将剩下的金蛋在原来的位置上又按1﹣1009编了号(即原来的2号变为1号,原来的4号变为2号……原来的2018号变为1009号),又从中取出新的编号为单数的金蛋进行检验,仍没有发现有奖金蛋……如此下去,检查到最后一枚金蛋才是有奖金蛋,问这枚有奖金蛋最初的编号是 .
16. 为了从2018枚外形相同的金蛋中找出唯一的有奖金蛋,检查员将这些金蛋按1﹣2018的顺序进行标号.第一次先取出编号为单数的金蛋,发现其中没有有奖金蛋,他将剩下的金蛋在原来的位置上又按1﹣1009编了号(即原来的2号变为1号,原来的4号变为2号……原来的2018号变为1009号),又从中取出新的编号为单数的金蛋进行检验,仍没有发现有奖金蛋……如此下去,检查到最后一枚金蛋才是有奖金蛋,问这枚有奖金蛋最初的编号是 .
17. 由沈康身教授所著,数学家吴文俊作序的《数学的魅力》一书中记载了这样一个故事:如图,三姐妹为了平分一块边长为1的祖传正方形地毯,先将地毯分割成七块,再拼成三个小正方形(阴影部分)。则图中AB的长应该是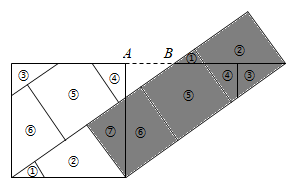 18. 某超市现有n个人在收银台排队等候结账.设结账人数按固定的速度增加,收银员结账的速度也是固定的.若同时开放2个收银台,需要20分钟可使排队等候人数为0;若同时开放3个收银台,需要12分钟可使排队等候人数为0.为减少顾客等待结账的时间,需要6分钟内使排队等候人数为0,则需要至少同时开放个收银台.19. 如图1,把一张标准纸一次又一次对折,得到“2开”纸、“4开”纸、“8开”纸、“16开”纸、…….当标准纸的短边长为a时.
18. 某超市现有n个人在收银台排队等候结账.设结账人数按固定的速度增加,收银员结账的速度也是固定的.若同时开放2个收银台,需要20分钟可使排队等候人数为0;若同时开放3个收银台,需要12分钟可使排队等候人数为0.为减少顾客等待结账的时间,需要6分钟内使排队等候人数为0,则需要至少同时开放个收银台.19. 如图1,把一张标准纸一次又一次对折,得到“2开”纸、“4开”纸、“8开”纸、“16开”纸、…….当标准纸的短边长为a时.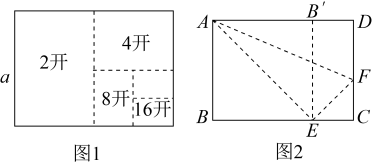 (1)、“16开”纸的短边长为(用含a的代数式表示).(2)、如图2,把这张标准纸对折得到的“16开”纸,按如下步骤折叠:
(1)、“16开”纸的短边长为(用含a的代数式表示).(2)、如图2,把这张标准纸对折得到的“16开”纸,按如下步骤折叠:第一步,将矩形的短边与长边对齐折叠,点B落在上的点处,铺平后得折痕;
第二步,将长边与折痕对齐折叠,点D正好与点E重合,铺平后得折痕 . 则:
①“16开”纸的长边长是(用含a的代数式表示);
②标准纸的长边与短边的比值是 .
三、解答题
-
20. 一个钢筋三角形架子的三边长分别是40cm,100cm,120cm,现要再做一个与其相似的钢筋三角形架子,而只有长为30cm和50cm的两根钢筋,要求以其中一根为一边,从另一根上截下两段(允许有余料)作为其余的两边.有几种不同的截法?21. 在倡议“绿色环保,公交出行”的活动中,学生小志对公交车的计价方式进行了研究.他发现北京公交集团的公交车站牌中都写有:“10公里以内(含)票价2元,每增加5公里以内(含)加价1元”,如下图.

小志查阅了相关资料,了解到北京公交车的票价按照乘客乘坐公交车的里程(公里)数计算,乘客可以按照如下方法计算票价:
①站牌中每一站上面标注的数字表示该站的站位号,乘客可以通过计算上、下车站的站位号的差,得到乘车的大致里程数,然后按照下面具体标准得出票价:若里程数在0至10之间(含0和10,下同),则票价为2元;若里程数在11至15之间,则票价为3元;若里程数在16至20之间,则票价为4元,以此类推.
②为了鼓励市民绿色出行,北京公交集团制定了票价优惠政策:使用市政公交一卡通刷卡,普通卡打5折,学生卡打2.5折.
请根据上述信息,回答下列问题:
(1)、学生甲想去抗战雕塑园参观,他乘坐339路公交车从云岗站上车,到抗战雕塑园站下车,那么原票价应为元,他使用学生卡实际支付元;(2)、学生乙使用学生卡乘339路公交车去北京西站,若下车刷卡时实际支付了1元,则他在佃起村上车的概率为 .22. 如图,某同学在物理课中设计了两种控制小灯泡的电路图,电源、小灯泡、开关和线路都能正常工作,按要求完成下列问题: (1)、如图1,电路图中有3个开关、、 , 随意闭合2个开关,求小灯泡能发光的概率;(2)、如图2,电路图中有2个开关、 , 两个开关中间有三条导线,每次旋转开关都能接通一条导线,若随意调整开关、 , 求小灯炮发光的概率.23. 用二维码(如图①)可以表示不同的信息,类似地,可通过在矩形网格中,对每一个小方格涂色或不涂色所得的图形来表示不同的信息.例如,网格中只有一个小方格,如图②,通过涂色或不涂色可表示两个不同的信息.
(1)、如图1,电路图中有3个开关、、 , 随意闭合2个开关,求小灯泡能发光的概率;(2)、如图2,电路图中有2个开关、 , 两个开关中间有三条导线,每次旋转开关都能接通一条导线,若随意调整开关、 , 求小灯炮发光的概率.23. 用二维码(如图①)可以表示不同的信息,类似地,可通过在矩形网格中,对每一个小方格涂色或不涂色所得的图形来表示不同的信息.例如,网格中只有一个小方格,如图②,通过涂色或不涂色可表示两个不同的信息. (1)、用画树状图或列表的方法,求图③可表示不同信息的总个数(图中标号1,2表示两个不同位置的小方格,下同).(2)、图④为2×2的网格图,它可表示不同信息的总个数为.(3)、某校需要给每位师生制作一张“校园出入证”,准备在证件的右下角采用n×n的网格图来表示个人身份信息.若该校师生共492人,则n的最小值为.
(1)、用画树状图或列表的方法,求图③可表示不同信息的总个数(图中标号1,2表示两个不同位置的小方格,下同).(2)、图④为2×2的网格图,它可表示不同信息的总个数为.(3)、某校需要给每位师生制作一张“校园出入证”,准备在证件的右下角采用n×n的网格图来表示个人身份信息.若该校师生共492人,则n的最小值为.四、实践探究题
-
24. 问题提出:
将一根长度是(的偶数)的细绳按照如图所示的方法对折次(),然后从重叠的细绳的一端开始,每隔1厘米(两端弯曲部分的绳长忽略不计)剪1刀,共剪刀(的整数),最后得到一些长和长的细绳.如果长的细绳有222根,那么原来的细绳的长度是多少?

问题探究:
为了解决问题,我们可以先从最简单的情形入手,再逐次递进,从中找出解决问题的方法.
探究一:
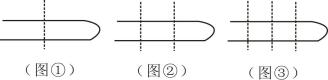
对折1次,可以看成有根绳子重叠在一起,如果剪1刀(如图①),左端出现了2根长的细绳,右端出现了根长的细绳,所以原绳长为;如果剪2刀(如图②),左端仍有2根长的细绳,中间有根长的细绳,右端仍有根长的细绳, 所以原绳长为;如果剪3刀(如图③),左端仍有2根长的细绳,中间有根长的细绳,右端仍有根长的细绳,所以原绳长为;以此类推,如果剪刀,左端仍有2根长的细绳,中间有根长细绳,右端仍有根长的细绳,所以,原绳长为 .
探究二:
对折2次,可以看成有根绳子重叠在一起,如果剪1刀(如图④),左端出现了2根长的细绳,两端共出现了根长的细绳,所以原绳长为;如果剪2刀(如图⑤),左端仍有2根长的细绳,中间有根长的细绳,两端仍有根长的细绳,所以原绳长为;如果剪3刀(如图⑥),左端仍有2根长的细绳,中间有根长的细绳,两端共有根长的细绳,所以原绳长为;以此类推,如果剪刀,左端仍有2根长的细绳,中间有根长的细绳,两端仍有根长的细绳,所以原绳长为 .

探究三:
对折3次(如图⑦),可以看成有根绳子重叠在一起,如果剪刀,左端有2根长的细绳,中间有根长的细绳,两端有根长的细绳,所以原绳长为cm.
 (1)、总结规律:
(1)、总结规律:对折次,可以看成有 根绳子重叠在一起,如果剪刀,左端有根长的细绳,中间会有根长的细绳,两端会有 根长的细绳,所以原绳长为 .
(2)、问题解决:如果长的细绳有222根,根据以上探究过程可以推算出细绳可能被对折了次,被剪了刀,原来的细绳的长度是 .
(3)、拓展应用:如果长的细绳有2024根,那么原来的细绳的长度是 .
25. 综合与实践在一次综合实践活动课上,王老师给每位同学各发了一张正方形纸片,请同学们思考如何仅通过折纸的方法来确定正方形一边上的一个三等分点.


【操作探究】
“乘风”小组的同学经过一番思考和讨论交流后,进行了如下操作:
第1步:如图1所示,先将正方形纸片ABCD对折,使点A与点B重合,然后展开铺平,折痕为EF;
第2步:将BC边沿CE翻折到GC的位置;
第3步:延长EG交AD于点H,则点H为AD边的三等分点.
证明过程如下:连接CH,
∵正方形ABCD沿CE折叠,
∴∠D=∠B=∠CGH=90°, ① ,
又∵CH=CH
∴△CGH≌△CDH,
∴GH=DH.
由题意可知E是AB的中点,设AB=6(个单位),DH=x,则AE=BE=EG=3,
在Rt△AEH中,可列方程: ② , (方程不要求化简)解得:DH= ③ , 即H是AD边的三等分点.
“破浪”小组是这样操作的:
第1步:如图2所示,先将正方形纸片对折,使点A与点B重合,然后展开铺平,折痕为EF;
第2步:再将正方形纸片对折,使点B与点D重合,再展开铺平,折痕为AC,沿DE翻折得折痕DE交AC于点G;
第3步:过点G折叠正方形纸片ABCD,使折痕MNIIAD.
【过程思考】
(1)、“乘风”小组的证明过程中,三个空的所填的内容分别是: ① , ②: , ③: ;(2)、结合“破浪”小组操作过程,判断点M是否为AB边的三等分点,并证明你的结论;(3)、【拓展提升】如图3,在菱形ABCD中,AB=5,BD=6,E是BD上的一个三等分点,记点D关于AE的对称点为D',射线ED'与菱形ABCD 的边交于点F,请直接写出D'F的长.26. 综合与实践中国旅游研究院2024年1月5日发布的“2024年冰雪旅游十佳城市”中,哈尔滨位列榜首,火爆出圈,其中帽儿山的滑雪运动深受欢迎.滑雪爱好者小李为了得出滑行距离(单位:m)与滑行时间(单位:s)之间的关系,以便更好地享受此项运动所带来的乐趣,他在滑道A上设置了若干个观测点,收集一些数据,如下表所示:
点位1
点位2
点位3
点位4
点位5
点位6
点位7
滑行时间
0
0.5
1
1.5
2
2.5
3
…
滑行距离
0
1.625
4.5
8.625
14
20.625
28.5
 (1)、请你在平面直角坐标系中描出表中数据所对应的7个点,并用平滑的曲线连接它们;(2)、观察由(1)所得的图象,请你依图象选用一个函数近似地表示与之间的函数关系,并求出这个近似函数的关系式(不要求写出自变量的取值范围);(3)、若另一名滑雪爱好者小张在小李出发5秒后沿着滑道B滑行(两条滑道互相平行,且起点在同一直线上),他的滑行距离(单位:m)与滑行时间(单位:s)可近似地看成二次函数 , 当小李滑行距离为384m时,他比小张多滑行的距离不超过160m,求的最小值.(参考数据:)27. 综合与实践
(1)、请你在平面直角坐标系中描出表中数据所对应的7个点,并用平滑的曲线连接它们;(2)、观察由(1)所得的图象,请你依图象选用一个函数近似地表示与之间的函数关系,并求出这个近似函数的关系式(不要求写出自变量的取值范围);(3)、若另一名滑雪爱好者小张在小李出发5秒后沿着滑道B滑行(两条滑道互相平行,且起点在同一直线上),他的滑行距离(单位:m)与滑行时间(单位:s)可近似地看成二次函数 , 当小李滑行距离为384m时,他比小张多滑行的距离不超过160m,求的最小值.(参考数据:)27. 综合与实践【发现问题】“速叠杯”是深受学生喜爱的一项运动,杯子的叠放方式如图1所示:每层都是杯口朝下排成一行,自下向上逐层递减一个杯子,直至顶层只有一个杯子,爱思考的小丽发现叠放所需杯子的总数随着第一层(最底层)杯子的个数变化而变化.
【提出问题】叠放所需杯子的总数y与第一层杯子的个数x之间有怎样的函数关系?
【分析问题】小丽结合实际操作和计算得到下表所示的数据:
第一层杯子的个数x
1
2
3
4
5
杯子的总数y
1
3
6
10
15
…
然后在平面直角坐标系中,描出上面表格中各对数值所对应的点,得到图2、小丽根据图2中点的分布情况,猜想其图象是二次函数图象的一部分;为了验证自己的猜想,小丽从“形”的角度出发.将要计算总数的杯子用黑色圆表示(如图3),再借助“补”的思想,补充相同数量的白色圆,使每层圆的数量相同,进而求出y与x的关系式.
 (1)、【解决问题】
(1)、【解决问题】直接写出与的关系式;
(2)、现有28个杯子,按【发现问题】中的方式叠放,求第一层怀了的个数;(3)、杯子的侧面展开图如图4所示,ND,MA分别为上、下底面圆的半径,所对的圆心角 . 将这样足够数量的杯子按【发现问题】中的方式叠放,但受桌面长度限制,第一层提放杯子的总长度不超过 , 求杯子叠放达到的最大高度和此时杯子的总数28. 数学实践活动,是一种非常有效的学习方式.通过活动可以激发我们的学习兴趣,提高动手动脑能力,拓展思推空间,丰富数学体验.让我们一起动手来折一折、转一转、剪一剪,体会活动带给我们的乐趣.折一折:将正方形纸片折叠,使边、都落在对角线上,展开得折痕、 , 连接 , 如图1.

转一转:将图1中的绕点旋转,使它的两边分别交边、于点、 , 连接 , 如图2.
剪一剪:将图3中的正方形纸片沿对角线剪开,如图4.
(1)、 , 写出图中两个等腰三角形:(不需要添加字母);(2)、线段、、之间的数量关系为;(3)、连接正方形对角线 , 若图2中的的边、分别交对角线于点、点 . 如图3,求的值;(4)、求证: .