2024年中考数学热点探究十九 数学古文化题
试卷更新日期:2024-04-27 类型:二轮复习
一、选择题(每题3分,共30分)
-
1. 我国古代典籍《周易》用“卦”描述万物的变化.下图为部分“卦”的符号,其中是中心对称图形的是( )A、
 B、
B、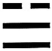 C、
C、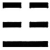 D、
D、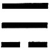 2. 甲骨文是我国古代的一种文字,是汉字的早期形式,反映了我国悠久的历史文化,体现了我国古代劳动人民的智慧,下列甲骨文中,不是轴对称图形的是( )A、
2. 甲骨文是我国古代的一种文字,是汉字的早期形式,反映了我国悠久的历史文化,体现了我国古代劳动人民的智慧,下列甲骨文中,不是轴对称图形的是( )A、 B、
B、 C、
C、 D、
D、 3. 我国古代数学的许多创新与发明都曾在世界上有重要影响.下列图形“杨辉三角”“中国七巧板”“刘微割圆术”“赵爽弦图”中,中心对称图形是( ).A、
3. 我国古代数学的许多创新与发明都曾在世界上有重要影响.下列图形“杨辉三角”“中国七巧板”“刘微割圆术”“赵爽弦图”中,中心对称图形是( ).A、 B、
B、 C、
C、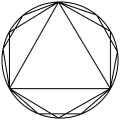 D、
D、 4. “斗”是我国古代称量粮食的量器,它无盖,其示意图如图所示,下列图形是“斗”的俯视图的是( )
4. “斗”是我国古代称量粮食的量器,它无盖,其示意图如图所示,下列图形是“斗”的俯视图的是( )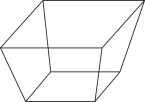 A、
A、 B、
B、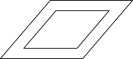 C、
C、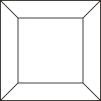 D、
D、 5. 榫卯是古代中国建筑、家具及其他器械的主要结构方式.如图,在某燕尾榫中,榫槽的横截面是梯形,其中 , , 燕尾角 , 外口宽 , 榫槽深度是 , 则它的里口宽为( )
5. 榫卯是古代中国建筑、家具及其他器械的主要结构方式.如图,在某燕尾榫中,榫槽的横截面是梯形,其中 , , 燕尾角 , 外口宽 , 榫槽深度是 , 则它的里口宽为( ) A、 B、 C、 D、6. 筒车是我国古代发明的一种水利灌溉工具,彰显了我国古代劳动人民的智慧,图1,点M表示筒车的一个盛水桶.如图2,当筒车工作时,盛水桶的运行路径是以轴心O为圆心,5m为半径的圆,且圆心在水面上方.若圆被水面截得的弦AB长为8m,则筒车工作时,盛水桶在水面以下的最大深度为( )
A、 B、 C、 D、6. 筒车是我国古代发明的一种水利灌溉工具,彰显了我国古代劳动人民的智慧,图1,点M表示筒车的一个盛水桶.如图2,当筒车工作时,盛水桶的运行路径是以轴心O为圆心,5m为半径的圆,且圆心在水面上方.若圆被水面截得的弦AB长为8m,则筒车工作时,盛水桶在水面以下的最大深度为( ) A、1米 B、2米 C、3米 D、4米7. 如图,等边三角形ABC内切的图形来自我国古代的太极图,等边三角形内切圆中的黑色部分和白色部分关于等边三角形ABC的内心成中心对称,则圆中的黑色部分的面积与△ABC的面积之比是( )
A、1米 B、2米 C、3米 D、4米7. 如图,等边三角形ABC内切的图形来自我国古代的太极图,等边三角形内切圆中的黑色部分和白色部分关于等边三角形ABC的内心成中心对称,则圆中的黑色部分的面积与△ABC的面积之比是( )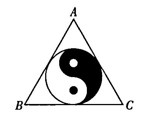 A、 B、 C、 D、8. 我国古代数学家刘徽利用圆内接正多边形创立了“割圆术”,现将半径为2的圆十二等分构造出2个矩形和1个正方形(如图),则阴影部分的面积是( )
A、 B、 C、 D、8. 我国古代数学家刘徽利用圆内接正多边形创立了“割圆术”,现将半径为2的圆十二等分构造出2个矩形和1个正方形(如图),则阴影部分的面积是( )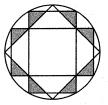 A、1 B、 C、 D、9. 如图是中国古代数学家赵爽用来证明勾股定理的弦图的示意图,它是由四个全等的直角三角形和一个小正方形EFGH组成,恰好拼成一个大正方形ABCD.连结EG并延长交BC于点M.若AB= ,EF=1,则GM的长为( )
A、1 B、 C、 D、9. 如图是中国古代数学家赵爽用来证明勾股定理的弦图的示意图,它是由四个全等的直角三角形和一个小正方形EFGH组成,恰好拼成一个大正方形ABCD.连结EG并延长交BC于点M.若AB= ,EF=1,则GM的长为( ) A、 B、 C、 D、10. 我国古代伟大的数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成一个正方形和两对全等的直角三角形,得到一个恒等式.后人借助这种分割方法所得的图形证明了勾股定理,如图所示的矩形由两个这样的图形拼成,若a=3,b=4,则该矩形的面积为( )
A、 B、 C、 D、10. 我国古代伟大的数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成一个正方形和两对全等的直角三角形,得到一个恒等式.后人借助这种分割方法所得的图形证明了勾股定理,如图所示的矩形由两个这样的图形拼成,若a=3,b=4,则该矩形的面积为( )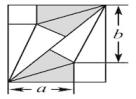 A、20 B、24 C、
A、20 B、24 C、 D、
D、
二、填空题(每题3分,共15分)
-
11. 如图,日晷是我国古代利用日影测定时刻的仪器,晷针在晷面上所形成的投影属于投影.
 12. 如图,筒车是我国古代发明的一种水利灌溉工具,彰显了我国古代劳动人民的智慧.点表示筒车的一个盛水桶.当筒车工作时,盛水桶的运行路径是以轴心(在水面上方)为圆心的圆,且圆的半径为5米.若筒车工作时,盛水桶在水面以下的最大深度为2米,则这个圆被水面截得的弦长为米.
12. 如图,筒车是我国古代发明的一种水利灌溉工具,彰显了我国古代劳动人民的智慧.点表示筒车的一个盛水桶.当筒车工作时,盛水桶的运行路径是以轴心(在水面上方)为圆心的圆,且圆的半径为5米.若筒车工作时,盛水桶在水面以下的最大深度为2米,则这个圆被水面截得的弦长为米. 13. 古代中国的数学专著《九章算术》中有一题:“今有生丝三十斤,千之,耗三斤十二两.今有干丝一十二斤,问生丝几何?“意思是:“今有生丝30斤,干燥后耗损3斤12两(古代中国1斤等于16两).今有干丝12斤,问原有生丝多少?”则原有生丝为斤.14. 我国古代数学家杨辉发现了如图所示的三角形,我们称之为“杨辉三角”,它具有一定的规律性,从图中取一列数:1,3,6,10,…,分别记为 , , , ,…,那么 的值是.
13. 古代中国的数学专著《九章算术》中有一题:“今有生丝三十斤,千之,耗三斤十二两.今有干丝一十二斤,问生丝几何?“意思是:“今有生丝30斤,干燥后耗损3斤12两(古代中国1斤等于16两).今有干丝12斤,问原有生丝多少?”则原有生丝为斤.14. 我国古代数学家杨辉发现了如图所示的三角形,我们称之为“杨辉三角”,它具有一定的规律性,从图中取一列数:1,3,6,10,…,分别记为 , , , ,…,那么 的值是.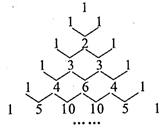 15. 如图1是将正方形分割成七个几何图形得到的七巧板,它是中国古代劳动人民发明的一种智力玩具.图2是由七巧板拼成“熊”的几何图形.四边形ABCD是菱形,且CIJ的面积为2,则AE= . 记点K到直线LG的距离为d,则 =
15. 如图1是将正方形分割成七个几何图形得到的七巧板,它是中国古代劳动人民发明的一种智力玩具.图2是由七巧板拼成“熊”的几何图形.四边形ABCD是菱形,且CIJ的面积为2,则AE= . 记点K到直线LG的距离为d,则 =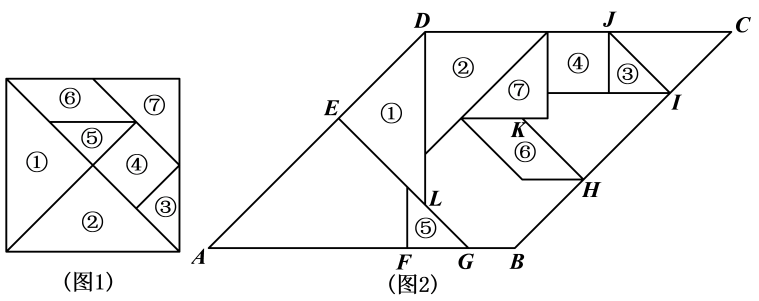
三、解答题(共9题,共59分)
-
16. 中国古代有着辉煌的数学成就,《周髀算经》《九章算术》《海岛算经》(孙子算经》等都是我国古代数学的重要文献.(1)、某班准备从这4部数学名著中随机选择2部作为数学文化课程学习内容,用适当的方法列举出所有可能的结果.(2)、求恰好选中《九章算术》和《孙子算经》的概率.17. 九章算术是中国古代算经十书最重要的一部,它的出现标志中国古代数学形成了完整的体系,其中有一道阐述“盈不足数”的问题,原文如下:今有人共买物,人出八,盈三;人出七,不足四其意思可以理解为现在有一些人共同买一个物品,如果每人出钱,还多出钱;如果每人出钱,则还差钱.(1)、若共同买这一物品的人数为人,则根据每人出钱,还多出钱,表示该物品的价格为 钱用含的式子表示;
(2)、计算购买个该物品所需的钱数.18. 中国古代在公元前⒉世纪就制成了世界上最早的潜望镜,西汉初年成书的《淮南万毕术》中有这样的记载:“取大镜高悬,恳水盆于其下,则见四邻矣”.如图1所示,其工作方法主要利用了光的反射原理. (1)、在图2中,AB呈水平状态,若入射角∠BCD=41°,∠CAE=37°(入射角等于反射角,CD,AE为法线),求∠ABC的度数.(2)、在(1)的条件下,若AB=11.2米.求点C到AB的距离(精确到0.1米,参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75).19. 图①是古代的一种远程投石机,其投出去的石块运动轨迹是抛物线的一部分.据《范蠡兵法》记载:“飞石重十二斤,为机发,行二百步”,其原理蕴含了物理中的“杠杆原理”.在如图②所示的平面直角坐标系中,将投石机置于斜坡的底部点处,石块从投石机竖直方向上的点处被投出,已知石块运动轨迹所在抛物线的顶点坐标是 .
(1)、在图2中,AB呈水平状态,若入射角∠BCD=41°,∠CAE=37°(入射角等于反射角,CD,AE为法线),求∠ABC的度数.(2)、在(1)的条件下,若AB=11.2米.求点C到AB的距离(精确到0.1米,参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75).19. 图①是古代的一种远程投石机,其投出去的石块运动轨迹是抛物线的一部分.据《范蠡兵法》记载:“飞石重十二斤,为机发,行二百步”,其原理蕴含了物理中的“杠杆原理”.在如图②所示的平面直角坐标系中,将投石机置于斜坡的底部点处,石块从投石机竖直方向上的点处被投出,已知石块运动轨迹所在抛物线的顶点坐标是 .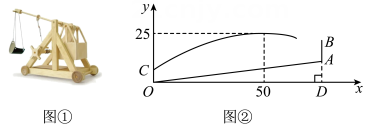 (1)、求抛物线的解析式;(2)、在斜坡上的点处建有垂直于水平线的城墙 , 且 , 点在一条直线上.通过计算说明石块能否飞越城墙 .20. 桑梯是我国古代劳动人民发明的一种采桑工具.图①是明朝科学家徐光启在《农政全书》中用图画描绘的桑梯,其示意图如图②所示,已知米,米.在安全使用的前提下,当时,桑梯顶端达到最大高度,求此时到地面的距离.(参考数据: , , , 精确到0.1米)
(1)、求抛物线的解析式;(2)、在斜坡上的点处建有垂直于水平线的城墙 , 且 , 点在一条直线上.通过计算说明石块能否飞越城墙 .20. 桑梯是我国古代劳动人民发明的一种采桑工具.图①是明朝科学家徐光启在《农政全书》中用图画描绘的桑梯,其示意图如图②所示,已知米,米.在安全使用的前提下,当时,桑梯顶端达到最大高度,求此时到地面的距离.(参考数据: , , , 精确到0.1米) 21. 桔槔俗称“吊杆”“称杆”(如图1),是我国古代农用工具,始见于墨子备城门 , 是一种利用杠杆原理的取水机械.如图2所示的是桔槔示意图,是垂直于水平地面的支撑杆,米,是杠杆,且米, . 当点A位于最高点时, .
21. 桔槔俗称“吊杆”“称杆”(如图1),是我国古代农用工具,始见于墨子备城门 , 是一种利用杠杆原理的取水机械.如图2所示的是桔槔示意图,是垂直于水平地面的支撑杆,米,是杠杆,且米, . 当点A位于最高点时, . (1)、求点A位于最高点时到地面的距离;(2)、当点A从最高点逆时针旋转54.5°到达最低点A1时,求此时水桶B上升的高度.
(1)、求点A位于最高点时到地面的距离;(2)、当点A从最高点逆时针旋转54.5°到达最低点A1时,求此时水桶B上升的高度.(考数据:)
22. 在古代,智慧的劳动人民已经会使用“石磨”,其原理为在磨盘的边缘连接一个固定长度的“杠杆”,推动“杠杆”带动磨盘转动,将粮食磨碎.如图,为圆的直径,是的一条弦,为弧的中点,作于点 , 交的延长线于点 , 连接 .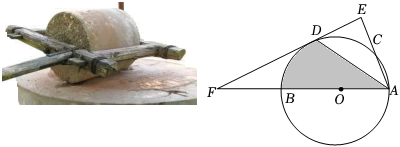 (1)、若 , 则圆心到“杠杆”的距离是多少?说明你的理由;(2)、若 , 求阴影部分的面积.结果保留23. “九宫图”传说是远古时代洛河中的一个神龟背上的图案,故又称“龟背图”,中国古代数学史上经常研究这一神话.数学上的“九宫图”所体现的是一个3×3表格,每行的三个数、每列的三个数、斜对角的三个数之和都相等,如图.
(1)、若 , 则圆心到“杠杆”的距离是多少?说明你的理由;(2)、若 , 求阴影部分的面积.结果保留23. “九宫图”传说是远古时代洛河中的一个神龟背上的图案,故又称“龟背图”,中国古代数学史上经常研究这一神话.数学上的“九宫图”所体现的是一个3×3表格,每行的三个数、每列的三个数、斜对角的三个数之和都相等,如图. (1)、求x;(2)、在剩下的5个格子里,请你再求出一个格子里的数.(指出某号格子,直接写出对应的数即可)24. 如图①,中国古代的马车已经涉及很复杂的机械设计(相对当时的生产力),包含大量零部件和工艺,所彰显的智慧让人拜服,如图②是马车的侧面示意图,为车轮的直径,过圆心的车架一端点着地时,地面与车轮相切于点 , 连接 .
(1)、求x;(2)、在剩下的5个格子里,请你再求出一个格子里的数.(指出某号格子,直接写出对应的数即可)24. 如图①,中国古代的马车已经涉及很复杂的机械设计(相对当时的生产力),包含大量零部件和工艺,所彰显的智慧让人拜服,如图②是马车的侧面示意图,为车轮的直径,过圆心的车架一端点着地时,地面与车轮相切于点 , 连接 . (1)、徽徽猜想 , 徽徽的猜想正确吗?请说明理由;(2)、若 , 米,求车轮的直径的长.
(1)、徽徽猜想 , 徽徽的猜想正确吗?请说明理由;(2)、若 , 米,求车轮的直径的长.四、实践探究题(共16分)
-
25. 【问题背景】
“刻漏”是我国古代的一种利用水流计时的工具.综合实践小组准备用甲、乙两个透明的坚直放置的容器和一根带节流阀(控制水的流速大小)的软管制作简易计时装置.
【实验操作】
综合实践小组设计了如下的实验:先在甲容器里加满水,此时水面高度为 , 开始放水后每隔观察一次甲容器中的水面高度,获得的数据如下表:

流水时间
0
10
20
30
40
水面高度(观察值)
30
29
28.1
27
25.8
(1)、任务1:分别计算表中每隔水面高度观察值的变化量;(2)、【建立模型】小组讨论发现:“”是初始状态下的准确数据,水面高度值的变化不均匀,但可以用一次函数近似地刻画水面高度与流水时间的关系.
任务2:利用时,时,这两组数据求水面高度与流水时间的函数解析式;
(3)、【反思优化】经检验,发现有两组表中观察值不满足任务2中求出的函数解析式,存在偏差.小组决定优化函数解析式,减少偏差.通过查阅资料后知道:为表中数据时,根据解析式求出所对应的函数值,计算这些函数值与对应的观察值之差的平方和,记为w;w越小,偏差越小.
任务3:①计算任务2得到的函数解析式的w值;
②请确定经过(0,30)的一次函数解析式,使得w的值最小;
(4)、【设计刻度】得到优化的函数解析式后,综合实践小组决定在甲容器外壁设计刻度,通过刻度直接读取时间.
任务4:请你简要写出时间刻度的设计方案.