2024年中考数学热点探究十五 学具操作问题
试卷更新日期:2024-04-27 类型:二轮复习
一、选择题(每题2分,共20分)
-
1. 一块三角板和一根直尺的位置如图所示,若 , 则的度数为( )
 A、 B、 C、 D、2. 把量角器和含角的三角板按如图方式摆放:零刻度线与长直角边重合,移动量角器使外圆弧与斜边相切时,发现中心恰好在刻度处,短直角边过量角器外沿刻度处(即 , ).则阴影部分的面积为( )
A、 B、 C、 D、2. 把量角器和含角的三角板按如图方式摆放:零刻度线与长直角边重合,移动量角器使外圆弧与斜边相切时,发现中心恰好在刻度处,短直角边过量角器外沿刻度处(即 , ).则阴影部分的面积为( )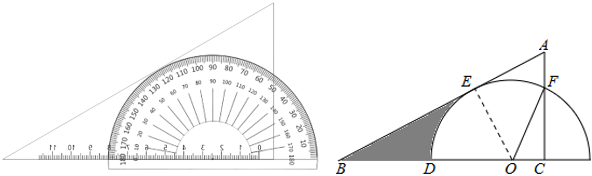 A、 B、 C、 D、3. 如图,在RtABC中,∠CAB=36°,斜边AC与量角器的直径重合(A点的刻度为0),将射线BF绕着点B转动,与量角器的外圆弧交于点D,与AC交于点E,若ABE是等腰三角形,则点D在量角器上对应的刻度为( )
A、 B、 C、 D、3. 如图,在RtABC中,∠CAB=36°,斜边AC与量角器的直径重合(A点的刻度为0),将射线BF绕着点B转动,与量角器的外圆弧交于点D,与AC交于点E,若ABE是等腰三角形,则点D在量角器上对应的刻度为( )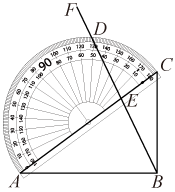 A、72° B、144° C、36°或72° D、72°或144°4. 如图,将直尺、含的直角三角尺和量角器按如图摆放,角的顶点A在直尺上读数为4,量角器与直尺的接触点B在直尺上的读数为7,量角器与直角三角尺的接触点为点C,则该量角器的直径是( ).
A、72° B、144° C、36°或72° D、72°或144°4. 如图,将直尺、含的直角三角尺和量角器按如图摆放,角的顶点A在直尺上读数为4,量角器与直尺的接触点B在直尺上的读数为7,量角器与直角三角尺的接触点为点C,则该量角器的直径是( ). A、3 B、 C、6 D、5. 小明制作简易工具来测量物体表面的倾斜程度,方法如下:将刻度重新设计的量角器固定在等腰直角三角板上,使量角器的刻度线与三角板的底边平行将用细线和铅锤做成的重锤线顶端固定在量角器中心点处,现将三角板底边紧贴被测物体表面,如图所示,此时重锤线在量角器上对应的刻度为 , 那么被测物体表面的倾斜角为( )
A、3 B、 C、6 D、5. 小明制作简易工具来测量物体表面的倾斜程度,方法如下:将刻度重新设计的量角器固定在等腰直角三角板上,使量角器的刻度线与三角板的底边平行将用细线和铅锤做成的重锤线顶端固定在量角器中心点处,现将三角板底边紧贴被测物体表面,如图所示,此时重锤线在量角器上对应的刻度为 , 那么被测物体表面的倾斜角为( ) A、 B、 C、 D、6. 如图,一个零刻度落在点A的量角器(半圆O),其直径为AB , 一等腰直角三角板MNB绕点B旋转,斜边BN交半圆O于点C , BM交半圆O于点D , 点C在量角器上的读数为.关于结论Ⅰ,Ⅱ,下列判断正确的是( )
A、 B、 C、 D、6. 如图,一个零刻度落在点A的量角器(半圆O),其直径为AB , 一等腰直角三角板MNB绕点B旋转,斜边BN交半圆O于点C , BM交半圆O于点D , 点C在量角器上的读数为.关于结论Ⅰ,Ⅱ,下列判断正确的是( )结论Ⅰ:;
结论Ⅱ:当边MN与半圆O相切于点E(点E在量角器上的读数为)时,
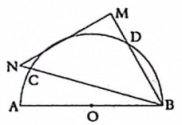 A、只有结论Ⅰ对 B、只有结论Ⅱ对 C、结论Ⅰ、Ⅱ都对 D、结论Ⅰ、Ⅱ都不对7. 如图,是利用一把直尺和一块三角尺ABC摆放并移动后得到的图形,其中 , , , 点A对应直尺的刻度为12,将该三角尺沿直尺边缘平移,使移动到 , 点对应直尺的刻度为0,则点C到的距离是( )
A、只有结论Ⅰ对 B、只有结论Ⅱ对 C、结论Ⅰ、Ⅱ都对 D、结论Ⅰ、Ⅱ都不对7. 如图,是利用一把直尺和一块三角尺ABC摆放并移动后得到的图形,其中 , , , 点A对应直尺的刻度为12,将该三角尺沿直尺边缘平移,使移动到 , 点对应直尺的刻度为0,则点C到的距离是( )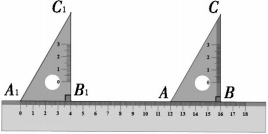 A、 B、 C、 D、8. 将一副直角三角板和一把宽度为2的直尺按如图方式摆放:先把60°和45°角的顶点及它们的直角边重合,再将此直角边垂直于直尺的上沿,重合的顶点落在直尺下沿上.这两个三角板的斜边分别交直尺上沿于A,B两点,则AB的长是( )
A、 B、 C、 D、8. 将一副直角三角板和一把宽度为2的直尺按如图方式摆放:先把60°和45°角的顶点及它们的直角边重合,再将此直角边垂直于直尺的上沿,重合的顶点落在直尺下沿上.这两个三角板的斜边分别交直尺上沿于A,B两点,则AB的长是( ) A、 B、 C、2 D、9. 如图,在中, , 直尺的一边与重合,另一边分别交 , 于点 , 点 , , 、处的读数分别为 , , , , 若直尺宽 , 则的长为( )
A、 B、 C、2 D、9. 如图,在中, , 直尺的一边与重合,另一边分别交 , 于点 , 点 , , 、处的读数分别为 , , , , 若直尺宽 , 则的长为( ) A、 B、 C、 D、10. 用直尺和圆规作Rt△ABC斜边AB上的高线CD,以下四个作图中,作法错误的是( )A、
A、 B、 C、 D、10. 用直尺和圆规作Rt△ABC斜边AB上的高线CD,以下四个作图中,作法错误的是( )A、 B、
B、 C、
C、 D、
D、
二、填空题(每题2分,共12分)
-
11. 如图,两个大小不同的量角器,小量角器由于长时间使用,某些刻度已经模糊不请,现将两个量角器的零刻度线放在同一直线上,使与C重合,如果弧与弧的公共点E在大量角器上对应的度数为 , 那么在小量角器上对应的度数为.
 12. 如图,量角器的零度刻度线为AB,将一矩形直尺与量角器部分重叠,使直尺一边与量角器相切于点C,直尺另一边交量角器于点A,D,量得AD=10cm,点D在量角器上的读数为120°,则该直尺的宽度为cm.
12. 如图,量角器的零度刻度线为AB,将一矩形直尺与量角器部分重叠,使直尺一边与量角器相切于点C,直尺另一边交量角器于点A,D,量得AD=10cm,点D在量角器上的读数为120°,则该直尺的宽度为cm. 13. 如图,某位同学用带有刻度的直尺在数轴上作图,若 , 点Q , 点M在直尺上,且分别与直尺上的刻度1和3对齐,在数轴上点N表示的数是10,则点P表示的数是 .
13. 如图,某位同学用带有刻度的直尺在数轴上作图,若 , 点Q , 点M在直尺上,且分别与直尺上的刻度1和3对齐,在数轴上点N表示的数是10,则点P表示的数是 . 14. 如图,将透明直尺叠放在正五边形之上,若正五边形有两个顶点在直尺的边上,且有一边与直尺的边垂直.则 °.
14. 如图,将透明直尺叠放在正五边形之上,若正五边形有两个顶点在直尺的边上,且有一边与直尺的边垂直.则 °.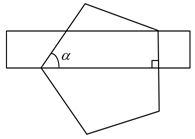 15. 如图,将一把矩形直尺和一块含角的三角板摆放在平面直角坐标系中,在轴上,点与点重合,点在上,三角板的直角边交于点 , 反比例函数的图象恰好经过点 , 若直尺的宽 , 三角板的斜边 , 则 .
15. 如图,将一把矩形直尺和一块含角的三角板摆放在平面直角坐标系中,在轴上,点与点重合,点在上,三角板的直角边交于点 , 反比例函数的图象恰好经过点 , 若直尺的宽 , 三角板的斜边 , 则 . 16. 图1是某个零件横截面的示意图,已知AB=CD,∠B=∠C,为了求出BC的长度,小艺将一根直尺按图2,图3,图4的三种方式摆放,所测得的具体数据(单位:cm)如图所示,则直尺宽为 cm,BC为 cm.
16. 图1是某个零件横截面的示意图,已知AB=CD,∠B=∠C,为了求出BC的长度,小艺将一根直尺按图2,图3,图4的三种方式摆放,所测得的具体数据(单位:cm)如图所示,则直尺宽为 cm,BC为 cm.
三、实践探究题(共10题,共88分)
-
17. 某校数学活动小组要测量校园内一棵古树的高度,王朵同学带领小组成员进行此项实践活动,记录如下:
填写人:王朵 综合实践活动报告 时间:2023年4月20日
活动任务:测量古树高度
活动过程
【步骤一】设计测量方案
小组成员讨论后,画出如图(1)的测量草图,确定需测的几何量.

【步骤二】准备测量工具
自制测角仪,把一根细线固定在半圆形量角器的圆心处,细线的另一端系一个小重物,制成一个简单的测角仪,利用它可以测量仰角或俯角,如图②所示.准备皮尺.

【步骤三】实地测量并记录数据
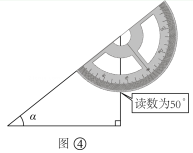
如图③,王朵同学站在离古树一定距离的地方,将这个仪器用手托起,拿到眼前,使视线沿着仪器的直径刚好到达古树的最高点.
如图④,利用测角仪,测量后计算得出仰角. ▲ .
测出眼睛到地面的距离AB.
测出所站地方到古树底部的距离BD.

【步骤四】计算古树高度CD.(结果精确到0.1m)
(参考数据:sin40°=0.643,cos40°=0.766,tan40°=0.839)
请结合图①、图④和相关数据写出α的度数并完成【步骤四】.
18. 【问题背景】
在一次数学实践活动中,张老师将班级学生分成“扶摇”、“惊鸿”、“骐骥”三个小组,运用直角三角尺测量三个不同直尺的宽度直尺的每两个长刻度之间的长度是
【实践探究】
(1)、扶摇组同学用含的三角尺,提出按照图的方案,直尺与直角三角尺的边重合,另一边分别交 , 于点 , 点 , , , 的读数分别为 , , , , 则该直尺的宽度的长为 ;
(2)、惊鸿组同学用含的三角尺,提出按照图的方案,直尺与直角三角尺的斜边重合,另一边分别交 , 于点 , 点 , , , 的读数分别为 , , , , 求该直尺的宽度;
(3)、骐骥组同学用含的三角尺,提出按照图的方案,直尺与直角三角尺斜平行,直分别交 , 于点 , , , 点 , , , 的读数分别为 , , , , , 直接写出该直尺的宽度结果精确到参考数据:19. 数学实验生活中,常常遇到需要测量物体长度、角度的情况,小聪同学思考:是否有既能测量长度,又能测量角度的多功能直尺?
小聪想自己做这样一把尺子:如图1,小聪准备了两条宽度为3cm的矩形纸带,并在点C处用可以转动的纽扣固定.小聪借助直角三角板的特殊度数,比较容易的找到表示 90°,60°,45°,30°角的刻度位置.那么另外的度数怎样标出呢?小聪开始思考原理:
 (1)、如图2,小聪将两条纸条叠合形成的四边形ABCD画出来,并分别作边DA , BA的延长线AF , AH . 小聪发现:①四边形ABCD是菱形;②∠FAH=2∠ACD . 请证明这两个结论.(2)、小聪发现,在(1)的基础上,表示 90°,60°,45°,30°角的刻度位置可以用三角形的边角关系表示出来,当∠FAH=90°时,∠ACD=45°,则有CE=AE=3cm , 因此表示 90°角的位置就可以通过计算找到.请利用小聪的思路,算出表示 60°角的位置与点C的距离(精确到0.01).(参考数据:≈1.414,≈1.732,).(3)、在以上思路启发下,小聪发现,在(1),(2)的基础上,对于任意位置的刻度的表示,只要完成三步任务:第一步,测量出直角△ACE 的直角边CE的长度m;第二步,计算出的值,这个值恰好是∠α 的正切值,即tanα=;第三步,利用计算器算出α的值,并在尺子上标出刻度即可.做出的尺子如图3所示.
(1)、如图2,小聪将两条纸条叠合形成的四边形ABCD画出来,并分别作边DA , BA的延长线AF , AH . 小聪发现:①四边形ABCD是菱形;②∠FAH=2∠ACD . 请证明这两个结论.(2)、小聪发现,在(1)的基础上,表示 90°,60°,45°,30°角的刻度位置可以用三角形的边角关系表示出来,当∠FAH=90°时,∠ACD=45°,则有CE=AE=3cm , 因此表示 90°角的位置就可以通过计算找到.请利用小聪的思路,算出表示 60°角的位置与点C的距离(精确到0.01).(参考数据:≈1.414,≈1.732,).(3)、在以上思路启发下,小聪发现,在(1),(2)的基础上,对于任意位置的刻度的表示,只要完成三步任务:第一步,测量出直角△ACE 的直角边CE的长度m;第二步,计算出的值,这个值恰好是∠α 的正切值,即tanα=;第三步,利用计算器算出α的值,并在尺子上标出刻度即可.做出的尺子如图3所示.请根据以上思路,计算出图2中CE的长度分别为4,2,1时,表示的角的刻度是多少(精确到分).
(参考数据:tan4°12'≈0.34,tan4°18'≈0.752,tan56°18'≈1.4994,tan56°24'≈1.5051,tan71°30'≈2.989,tan71°36'≈3.006).
20. 问题情境:在Rt△ABC中,∠BAC=90°,AB=6,AC=8.直角三角板EDF中∠EDF=90°,将三角板的直角顶点D放在Rt△ABC斜边BC的中点处,并将三角板绕点D旋转,三角板的两边DE , DF分别与边AB , AC交于点M , N . (1)、猜想证明:
(1)、猜想证明:如图①,在三角板旋转过程中,当点M为边AB的中点时,试判断四边形AMDN的形状,并说明理由;
(2)、问题解决:如图②,在三角板旋转过程中,当∠B=∠MDB时,求线段CN的长.
21. 某校数学活动小组要测量校园内一棵古树的高度,王朵同学带领小组成员进行此项实践活动,记录如下:填写人:王朵 综合实践活动报告 时间:2023年4月20日
活动任务:测量古树高度
活动过程
【步骤一】设计测量方案
小组成员讨论后,画出如图①的测量草图,确定需测的几何量.

【步骤二】准备测量工具
自制测角仪,把一根细线固定在半圆形量角器的圆心处,细线的另一端系一个小重物,制成一个简单的测角仪,利用它可以测量仰角或俯角,如图②所示准备皮尺.

【步骤三】实地测量并记录数据如图③,王朵同学站在离古树一定距离的地方,将这个仪器用手托起,拿到眼前,使视线沿着仪器的直径刚好到达古树的最高点.
如图④,利用测角仪,测量后计算得出仰角 .
测出眼睛到地面的距离 .
测出所站地方到古树底部的距离 .

 .
..
.
【步骤四】计算古树高度 . (结果精确到)
(参考数据:)
请结合图①、图④和相关数据写出的度数并完成【步骤四】.
22. 有一根长方形直尺宽为4cm,长为10cm,还有一块锐角为45°的直角三角板,它的斜边长为16cm,如图,将直尺的宽DE与直角三角板的斜边AB重合,且点D与点A重合,将直尺沿射线AB方向平移,设平移的长度为xcm,且直尺和三角板重叠部分的面积为Scm2 ,
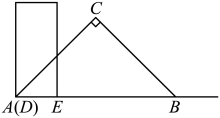 (1)、当直角顶点C落在直尺的长上时,x=cm;(2)、当0<x<12时,求S与x之间的函数关系式;(3)、是否存在一个位置,使重叠部分面积为28cm2?若存在直接写出x的值,若不存在,请说明理由。23. 某综合实践研究小组为了测量观察目标时的仰角和俯角,利用量角器和铅锤自制了一个简易测角仪,如图1所示.
(1)、当直角顶点C落在直尺的长上时,x=cm;(2)、当0<x<12时,求S与x之间的函数关系式;(3)、是否存在一个位置,使重叠部分面积为28cm2?若存在直接写出x的值,若不存在,请说明理由。23. 某综合实践研究小组为了测量观察目标时的仰角和俯角,利用量角器和铅锤自制了一个简易测角仪,如图1所示. (1)、如图2,在点观察所测物体最高点 , 当量角器零刻度线上两点均在视线上时,测得视线与铅垂线所夹的锐角为 , 设仰角为 , 请直接用含的代数式示 .(2)、如图3,为了测量广场上空气球离地面的高度,该小组利用自制简易测角仪在点分别测得气球的仰角为 , 为 , 地面上点在同一水平直线上, , 求气球离地面的高度 . (参考数据: , )24. 如图1,水平放置一个三角板和一个量角器,三角板的边AB和量角器的直径DE在一条直线上,AB=BC=6cm,OD=3cm,开始的时候BD=1cm,现在三角板以2cm/s的速度向右移动.
(1)、如图2,在点观察所测物体最高点 , 当量角器零刻度线上两点均在视线上时,测得视线与铅垂线所夹的锐角为 , 设仰角为 , 请直接用含的代数式示 .(2)、如图3,为了测量广场上空气球离地面的高度,该小组利用自制简易测角仪在点分别测得气球的仰角为 , 为 , 地面上点在同一水平直线上, , 求气球离地面的高度 . (参考数据: , )24. 如图1,水平放置一个三角板和一个量角器,三角板的边AB和量角器的直径DE在一条直线上,AB=BC=6cm,OD=3cm,开始的时候BD=1cm,现在三角板以2cm/s的速度向右移动.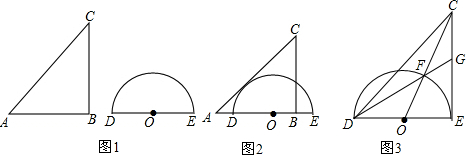 (1)、当B与O重合的时候,求三角板运动的时间;(2)、如图2,当AC与半圆相切时,求AD;(3)、如图3,当AB和DE重合时,求证:=CG·CE.25. 应用与探究
(1)、当B与O重合的时候,求三角板运动的时间;(2)、如图2,当AC与半圆相切时,求AD;(3)、如图3,当AB和DE重合时,求证:=CG·CE.25. 应用与探究【情境呈现】
在一次数学兴趣小组活动中,小明同学将一大一小两个三角板按照如图1所示的方式摆放,其中 , , . 他把三角板固定好后,将三角板从图1所示的位置开始绕点按顺时针方向旋转,每秒转动 , 设转动时间为秒 .
 (1)、【问题应用】请直接写出图1中线段的值;(2)、如图2,在三角板旋转的过程中,连接 , 当四边形是矩形时,求值;(3)、【问题探究】如图3,在三角板旋转的过程中,取的中点 , 连接 , 是否存在最大值?若存在,请求出的最大值,并直接写出此时的值:若不存在,请说明理由.26. 综合与实践
(1)、【问题应用】请直接写出图1中线段的值;(2)、如图2,在三角板旋转的过程中,连接 , 当四边形是矩形时,求值;(3)、【问题探究】如图3,在三角板旋转的过程中,取的中点 , 连接 , 是否存在最大值?若存在,请求出的最大值,并直接写出此时的值:若不存在,请说明理由.26. 综合与实践综合与实践课上,老师让同学们以“三角板的平移”为主题开展数学活动.
 (1)、操作判断
(1)、操作判断操作一:将一副等腰直角三角板两斜边重合,按图1放置;
操作二:将三角板沿方向平移(两三角板始终接触)至图2位置.
根据以上操作,填空:
①图1中四边形的形状是;
②图2中与的数量关系是;四边形的形状是 .
(2)、迁移探究小航将一副等腰直角三角板换成一副含角的直角三角板,继续探究,已知三角板边长为 , 过程如下:
将三角板按(1)中的方式操作,如图3,在平移过程中,四边形的形状能否是菱形,若不能,请说明理由,若能,请求出的长.
(3)、拓展应用在(2)的探究过程中:
①当为等腰三角形时,请直接写出的长;
②直接写出的最小值.