2024年中考数学热点探究十四 折叠问题
试卷更新日期:2024-04-27 类型:二轮复习
一、选择题(每题3分,共30分)
-
1. 如图,在矩形ABCD中,点E在DC上,将矩形沿AE折叠,使点D落在BC边上的点F处,若AB=6,BC=10,则tan∠EAF的值为( )
 A、 B、 C、 D、2. 如图,三角形纸片ABC,点D是BC边上一点,连接AD,把△ABD沿着AD翻折,得到△AED,DE与AC交于点G,连接BE交AD于点F.若DG=GE,AF=3,BF=2,△ADG的面积为2,则点F到BC的距离为( )
A、 B、 C、 D、2. 如图,三角形纸片ABC,点D是BC边上一点,连接AD,把△ABD沿着AD翻折,得到△AED,DE与AC交于点G,连接BE交AD于点F.若DG=GE,AF=3,BF=2,△ADG的面积为2,则点F到BC的距离为( ) A、 B、 C、 D、3. 如图,在矩形中,点为的中点,将沿所在直线翻折压平,得到 , 延长与交于点 , 若 , , 则四边形的面积为( )
A、 B、 C、 D、3. 如图,在矩形中,点为的中点,将沿所在直线翻折压平,得到 , 延长与交于点 , 若 , , 则四边形的面积为( ) A、 B、 C、 D、4. 如图,是一条弦,将劣弧沿弦翻折,连结并延长交翻折后的弧于点 , 连结 , 若 , 则的长为( )
A、 B、 C、 D、4. 如图,是一条弦,将劣弧沿弦翻折,连结并延长交翻折后的弧于点 , 连结 , 若 , 则的长为( )
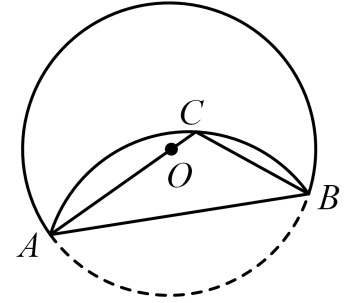 A、 B、 C、 D、5. 如图,矩形纸片 , 满足 , 将此矩形纸片按下面顺序折叠,则图4中的长为(用含的代数式表示)( )
A、 B、 C、 D、5. 如图,矩形纸片 , 满足 , 将此矩形纸片按下面顺序折叠,则图4中的长为(用含的代数式表示)( ) A、 B、 C、 D、6. 意大利著名画家达·芬奇用如图所示的方法证明了勾股定理,图2是将图1沿直线剪开,将右半部分上下翻转得到的图形,其中四边形 , 四边形与四边形均为正方形,若图1中空白部分面积为37,线段的长为7,则图2中两个直角三角形的面积和为( )
A、 B、 C、 D、6. 意大利著名画家达·芬奇用如图所示的方法证明了勾股定理,图2是将图1沿直线剪开,将右半部分上下翻转得到的图形,其中四边形 , 四边形与四边形均为正方形,若图1中空白部分面积为37,线段的长为7,则图2中两个直角三角形的面积和为( ) A、6 B、12 C、15 D、257. 如图,将正方形纸片的和进行折叠,使两个直角的顶点重合于对角线上的点P处、分别是折痕,若点P沿从点B向点D移动,则阴影部分的周长( )
A、6 B、12 C、15 D、257. 如图,将正方形纸片的和进行折叠,使两个直角的顶点重合于对角线上的点P处、分别是折痕,若点P沿从点B向点D移动,则阴影部分的周长( )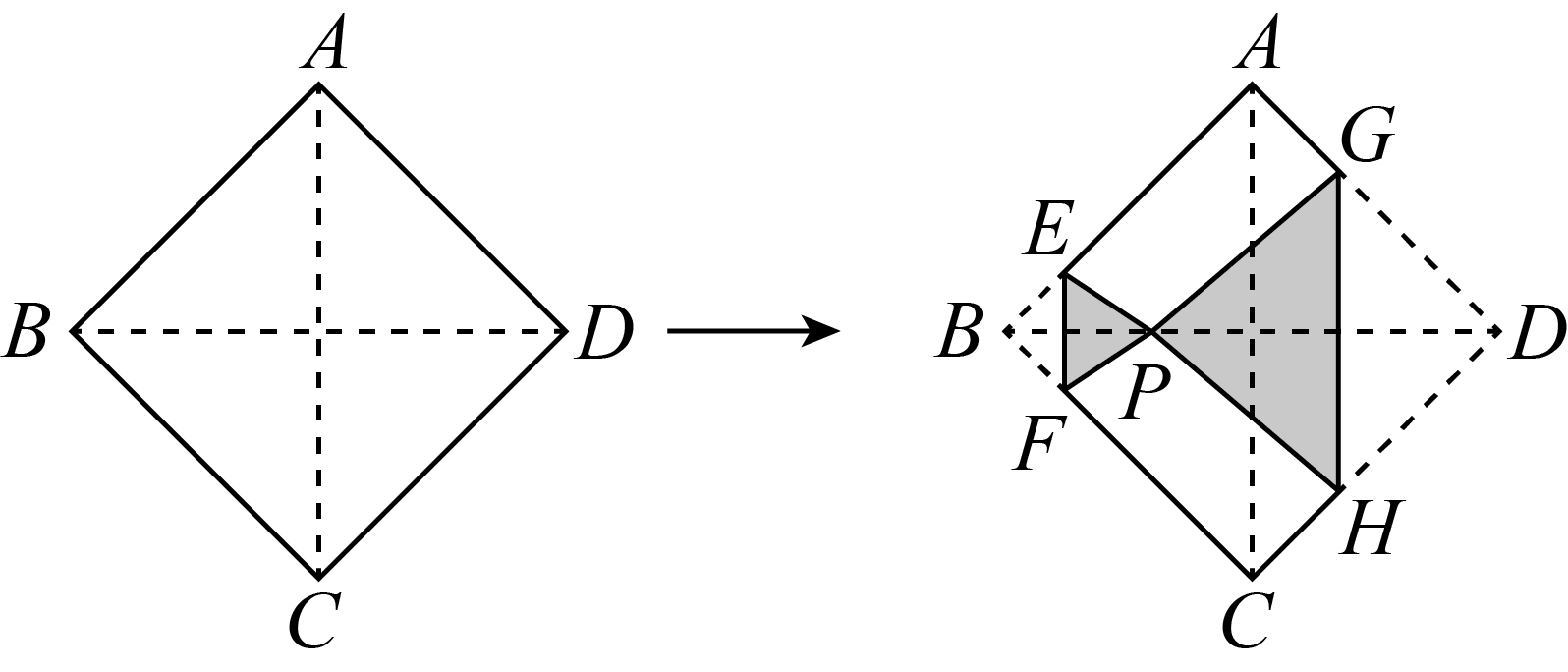 A、先变大,后变小 B、先变小,后变大 C、当占P在中点处时,阴影部分周长最大 D、保持不变8. 如图,为的直径,将沿翻折,翻折后的弧交于D.若 , , 则图中阴影部分的面积为( )
A、先变大,后变小 B、先变小,后变大 C、当占P在中点处时,阴影部分周长最大 D、保持不变8. 如图,为的直径,将沿翻折,翻折后的弧交于D.若 , , 则图中阴影部分的面积为( ) A、 B、 C、8 D、109. 如图,在平面直角坐标系中,矩形的边 . , 将矩形沿直线折叠到如图所示的位置,线段恰好经过点 , 点落在轴的点位置,点的坐标是
A、 B、 C、8 D、109. 如图,在平面直角坐标系中,矩形的边 . , 将矩形沿直线折叠到如图所示的位置,线段恰好经过点 , 点落在轴的点位置,点的坐标是 A、 B、 C、 , D、 ,10. 如图,正方形的边长为4,点是边上的一点,将沿着折叠至 , 若、恰好与正方形的中心为圆心的相切,则折痕的长为( )
A、 B、 C、 , D、 ,10. 如图,正方形的边长为4,点是边上的一点,将沿着折叠至 , 若、恰好与正方形的中心为圆心的相切,则折痕的长为( ) A、 B、5 C、 D、以上都不对
A、 B、5 C、 D、以上都不对二、填空题(每题3分,共15分)
-
11. 在△ABC中, , , 点D是边上一动点,将△ACD沿直线翻折,使点A落在点E处,连接交于点F(所给图形仅仅是示意图).当△DEF是直角三角形时, .
 12. 如图,在矩形中, , , 点、分别在、上,连接、 , 将矩形沿折叠,使点落在边上的点处,沿折叠,使点落在上的点处,延长交于点 , 连接 , 则的面积为 .
12. 如图,在矩形中, , , 点、分别在、上,连接、 , 将矩形沿折叠,使点落在边上的点处,沿折叠,使点落在上的点处,延长交于点 , 连接 , 则的面积为 . 13. 如图,在菱形ABCD中,点在BC上,将沿AE折叠得到 , 点在BC的延长线上,AG与CD相交于点.若 , 则的值为.
13. 如图,在菱形ABCD中,点在BC上,将沿AE折叠得到 , 点在BC的延长线上,AG与CD相交于点.若 , 则的值为. 14. 如图,在中,D为斜边的中点,点E在边上,将沿叠至 . 若的延长线经过点D , 平分 , , 则的值为 , 的长为 .
14. 如图,在中,D为斜边的中点,点E在边上,将沿叠至 . 若的延长线经过点D , 平分 , , 则的值为 , 的长为 . 15. 如图,在矩形ABCD中, AB=3, AD=4, 点P 是边AD上的一个动点(点P不与点A, D重合),将△BAP沿BP折叠, 使点A落在点A'的位置, 连接AA', DA', 若AA' = DA', 则AP 的长为 .
15. 如图,在矩形ABCD中, AB=3, AD=4, 点P 是边AD上的一个动点(点P不与点A, D重合),将△BAP沿BP折叠, 使点A落在点A'的位置, 连接AA', DA', 若AA' = DA', 则AP 的长为 .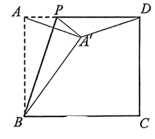
三、解答题(共5题,共40分)
-
16. 我们知道:如图①,点B把线段AC分成两部分,如果 , 那么称点B为线段AC的黄金分割点.它们的比值为.
图①
 图②
图② 图③
图③ (1)、在图①中,若 , 则AB的长为cm;(2)、如图②,用边长为20cm的正方形纸片进行如下操作:对折正方形ABCD得折痕EF , 连接CE , 将CB折叠到CE上,点B的对应点H , 得折痕CG.试说明:G是AB的黄金分割点;(3)、如图③,小明进一步探究:在边长为a的正方形ABCD的边AD上任取点E(),连接BE , 作 , 交AB于点F , 延长EF , CB交于点P.他发现当PB与BC满足某种关系时,E , F恰好分别是AD , AB的黄金分割点.请猜想小明的发现,并说明理由.17. 如图,为的中线,以为直角边在其右侧作直角 , , 与交于点F , .
(1)、在图①中,若 , 则AB的长为cm;(2)、如图②,用边长为20cm的正方形纸片进行如下操作:对折正方形ABCD得折痕EF , 连接CE , 将CB折叠到CE上,点B的对应点H , 得折痕CG.试说明:G是AB的黄金分割点;(3)、如图③,小明进一步探究:在边长为a的正方形ABCD的边AD上任取点E(),连接BE , 作 , 交AB于点F , 延长EF , CB交于点P.他发现当PB与BC满足某种关系时,E , F恰好分别是AD , AB的黄金分割点.请猜想小明的发现,并说明理由.17. 如图,为的中线,以为直角边在其右侧作直角 , , 与交于点F , . (1)、如图1,若 , 求的长;(2)、如图2,若将绕点C逆时针旋转得到 , 连接、 , 探究、的数量关系,并说明理由;(3)、如图3,若 , , , 直线上有一点M , 连接 , 将沿着翻折到所在的平面内得到 , 取的中点P , 连接 , 当最小时,请直接写出的面积.18. 在中, , , 为平面内的一点.
(1)、如图1,若 , 求的长;(2)、如图2,若将绕点C逆时针旋转得到 , 连接、 , 探究、的数量关系,并说明理由;(3)、如图3,若 , , , 直线上有一点M , 连接 , 将沿着翻折到所在的平面内得到 , 取的中点P , 连接 , 当最小时,请直接写出的面积.18. 在中, , , 为平面内的一点.图1
 图2
图2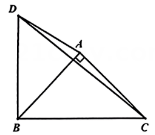 图3
图3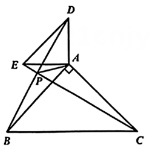 (1)、如图1,当点在边上时, , 且 , 求的长;(2)、如图2,当点在的外部,且满足 , 求证:;(3)、如图3, , 当、分别为、的中点时,把绕点顺时针旋转,设旋转角为 , 直线与的交点为 , 连接 , 直接写出旋转中面积的最大值.19. 定义:对多边形进行折叠,若翻折后的图形恰能拼成一个无缝隙、无重叠的四边形,则这样的四边形称为镶嵌四边形.
(1)、如图1,当点在边上时, , 且 , 求的长;(2)、如图2,当点在的外部,且满足 , 求证:;(3)、如图3, , 当、分别为、的中点时,把绕点顺时针旋转,设旋转角为 , 直线与的交点为 , 连接 , 直接写出旋转中面积的最大值.19. 定义:对多边形进行折叠,若翻折后的图形恰能拼成一个无缝隙、无重叠的四边形,则这样的四边形称为镶嵌四边形. (1)、如图1,将纸片沿中位线折叠,使点落在边上的处,再将纸片分别沿 , 折叠,使点和点都与点重合,得到双层四边形 , 则双层四边形为形.(2)、纸片按图2的方式折叠,折成双层四边形为矩形,若 , , 求的长.(3)、如图3,四边形纸片满足 , , , , . 把该纸片折叠,得到双层四边形为正方形.请你画出一种折叠的示意图,并直接写出此时的长.20. 在中,D为AB边上一点,过点D作交AC于点E , 以DE为折线,将翻折,设所得的与梯形DBCE重叠部分的面积为y.
(1)、如图1,将纸片沿中位线折叠,使点落在边上的处,再将纸片分别沿 , 折叠,使点和点都与点重合,得到双层四边形 , 则双层四边形为形.(2)、纸片按图2的方式折叠,折成双层四边形为矩形,若 , , 求的长.(3)、如图3,四边形纸片满足 , , , , . 把该纸片折叠,得到双层四边形为正方形.请你画出一种折叠的示意图,并直接写出此时的长.20. 在中,D为AB边上一点,过点D作交AC于点E , 以DE为折线,将翻折,设所得的与梯形DBCE重叠部分的面积为y.图1
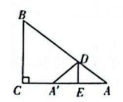 图2
图2  图3
图3 (1)、如图1,若 , , , , 则y的值为;(2)、如图2,若 , , D为AB中点,则y的值为;(3)、若 , , , 设.
(1)、如图1,若 , , , , 则y的值为;(2)、如图2,若 , , D为AB中点,则y的值为;(3)、若 , , , 设.①求y与x的函数解析式;
②y是否有最大值,若有,求出y的最大值;若没有,请说明理由.
四、实践探究题(共4题,共35分)
-
21. 综合与实践:

问题背景:数学小组发现国旗上五角星的五个角都是顶角为的等腰三角形,对此三角形产生了极大兴趣并展开探究.
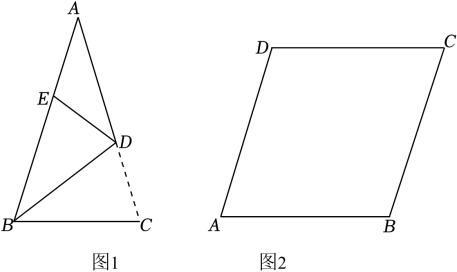
探究发现:如图1,在中, , .
(1)、操作发现:将折叠,使边落在边上,点的对应点是点 , 折痕交于点 , 连接 , ,①;
②设 , 则(用含的式子表示);
(2)、进一步探究发现: , 这个比值被称为黄金比.请你在(1)的条件下,证明: .(3)、拓展应用:当等腰三角形的底与腰的比等于黄金比时,这个三角形叫黄金三角形.如图1中的是黄金三角形.
如图2,在菱形中, , , 求菱形较长对角线的长.
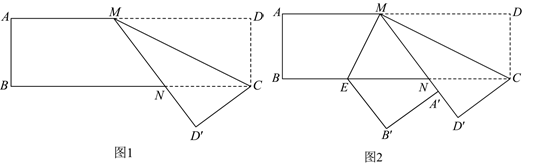
22. 折叠问题是我们常见的数学问题,它是利用图形变化的轴对称性质解决的相关问题.数学活动课上,同学们以“矩形的折叠”为主题开展了数学活动.【操作】如图1,在矩形中,点M在边上,将矩形纸片沿所在的直线折叠,使点D落在点处,与交于点N .
【猜想】
(1)、【验证】请将下列证明过程补充完整:∵矩形纸片沿所在的直线折叠
∴
∵四边形是矩形
∴(矩形的对边平行)
∴()
∴(等量代换)
∴()
(2)、【应用】如图2,继续将矩形纸片折叠,使恰好落在直线上,点A落在点处,点B落在点处,折痕为 .
⑴猜想与的数量关系,并说明理由;
⑵若 , , 求的长.
23.(1)、【探究发现】如图①所示,在正方形中,为边上一点,将沿翻折到处,延长交边于点.求证: (2)、【类比迁移】如图②,在矩形中,为边上一点,且将沿翻折到处,延长交边于点延长交边于点且求的长.
(2)、【类比迁移】如图②,在矩形中,为边上一点,且将沿翻折到处,延长交边于点延长交边于点且求的长. (3)、【拓展应用】如图③,在菱形中, , 为边上的三等分点,将沿翻折得到 , 直线交于点求的长.
(3)、【拓展应用】如图③,在菱形中, , 为边上的三等分点,将沿翻折得到 , 直线交于点求的长. 24. 综合与实践
24. 综合与实践 (1)、【操作发现】如图1,诸葛小组将正方形纸片ABCD沿过点A的直线折叠,使点B落在正方形内部的点M处,折痕为AE , 再将纸片沿过点A的直线折叠,使AD与AM重合,折痕为AF , 求∠EAF的正切值;(2)、【拓展探究】如图2,孔明小组继续将正方形纸片沿EF继续折叠,点C的对应点恰好落在折痕AE上的点N处,连接NF交AM于点P , 若 , 求线段PM的长;(3)、【迁移应用】如图3,在矩形ABCD中,点E , F分别在边BC , CD上,将矩形ABCD沿AE , AF折叠,点B落在点M处,点D落在点G处,点A , M , G恰好在同一直线上,若点F为CD的三等分点,AB=3,AD=5,请求出线段BE的长.
(1)、【操作发现】如图1,诸葛小组将正方形纸片ABCD沿过点A的直线折叠,使点B落在正方形内部的点M处,折痕为AE , 再将纸片沿过点A的直线折叠,使AD与AM重合,折痕为AF , 求∠EAF的正切值;(2)、【拓展探究】如图2,孔明小组继续将正方形纸片沿EF继续折叠,点C的对应点恰好落在折痕AE上的点N处,连接NF交AM于点P , 若 , 求线段PM的长;(3)、【迁移应用】如图3,在矩形ABCD中,点E , F分别在边BC , CD上,将矩形ABCD沿AE , AF折叠,点B落在点M处,点D落在点G处,点A , M , G恰好在同一直线上,若点F为CD的三等分点,AB=3,AD=5,请求出线段BE的长.