2024年中考数学热点探究十三 格点图中的作图与计算问题
试卷更新日期:2024-04-27 类型:二轮复习
一、作图题
-
1. 如图在
 的网格中,
的网格中, 的顶点都在格点上.仅用无刻度的直尺在给定的网格中分别按下列要求画图.(请保留画图痕迹,画图过程用虚线表示,画图结果用实线表示)
的顶点都在格点上.仅用无刻度的直尺在给定的网格中分别按下列要求画图.(请保留画图痕迹,画图过程用虚线表示,画图结果用实线表示) (1)、在图1中,画出
(1)、在图1中,画出 的重心G; (2)、在图2中,画线段
的重心G; (2)、在图2中,画线段 , 点E在
, 点E在 上,使得
上,使得 ; (3)、图3中,在
; (3)、图3中,在 内寻找一格点N,使∠ANB=2∠C。并标注点N的位置。 2. 如图,在的正方形网格中,每个小正方形的顶点称为格点,的顶点均在格点上.按要求完成下列画图.(要求:用无刻度直尺,保留必要的画图痕迹,不写画法)
内寻找一格点N,使∠ANB=2∠C。并标注点N的位置。 2. 如图,在的正方形网格中,每个小正方形的顶点称为格点,的顶点均在格点上.按要求完成下列画图.(要求:用无刻度直尺,保留必要的画图痕迹,不写画法)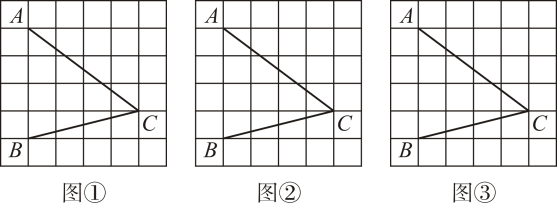 (1)、在图①中画出一个 , 使 , D为格点(点D不在点C处):(2)、在图②中的边BC上找一点E , 连接AE , 使;(3)、在图③中的边BC上找一点F , 使点F到AB和AC所在直线的距离相等.3. 如图,在由边长为1的小正方形构成的6×8的网格中,△ABC的顶点A,B,C均在格点上.请按要求完成作图:①仅用无刻度直尺;②保留作图痕迹并标注相关字母.
(1)、在图①中画出一个 , 使 , D为格点(点D不在点C处):(2)、在图②中的边BC上找一点E , 连接AE , 使;(3)、在图③中的边BC上找一点F , 使点F到AB和AC所在直线的距离相等.3. 如图,在由边长为1的小正方形构成的6×8的网格中,△ABC的顶点A,B,C均在格点上.请按要求完成作图:①仅用无刻度直尺;②保留作图痕迹并标注相关字母. (1)、如图1,在线段AC上找一点D,使得.(2)、如图2,画出△ABC的角平分线BE.4. 如图①,图②,图③均是5×5的正方形网格,每个小正方形的边长均为1,每个小正方形的顶点称为格点,点A , B均在格点上.在图①,图②,图③中,只用无刻度的直尺,在给定的网格中按要求作图,所画图形的顶点均在格点上.
(1)、如图1,在线段AC上找一点D,使得.(2)、如图2,画出△ABC的角平分线BE.4. 如图①,图②,图③均是5×5的正方形网格,每个小正方形的边长均为1,每个小正方形的顶点称为格点,点A , B均在格点上.在图①,图②,图③中,只用无刻度的直尺,在给定的网格中按要求作图,所画图形的顶点均在格点上. (1)、在图①中,找一个格点C , 使AC=BC .(2)、在图②中,以AB为直角边画等腰直角三角形ABD(画出一个即可).(3)、在图③中,画锐角三角形ABE , 使∠AEB=45°(画出一个即可).5. 如图是由小正方形组成的6×7网格,每个小正方形的边长为1,每个小正方形的顶点称为格点.格点A、B、C在同一个圆上,只用无刻度直尺在分别在给定网格中按照下列要求作图,保留作图痕迹.
(1)、在图①中,找一个格点C , 使AC=BC .(2)、在图②中,以AB为直角边画等腰直角三角形ABD(画出一个即可).(3)、在图③中,画锐角三角形ABE , 使∠AEB=45°(画出一个即可).5. 如图是由小正方形组成的6×7网格,每个小正方形的边长为1,每个小正方形的顶点称为格点.格点A、B、C在同一个圆上,只用无刻度直尺在分别在给定网格中按照下列要求作图,保留作图痕迹. (1)、图①中,先画出圆心O , 然后在上画点D , 使 .(2)、图②中,在弧BC上画点E , 连接AE , 使AE平分∠CAB .6. 如图,是由边长为1的小正方形构成的6×6网格,每个小正方形的顶点叫做格点,⊙O经过A、B、C、D四个格点,仅用无刻度的直尺在给定的网格中按要求画图(画图过程中起辅助作用的用虚线表示,画图结果用实线表示,并用黑色水笔描黑)
(1)、图①中,先画出圆心O , 然后在上画点D , 使 .(2)、图②中,在弧BC上画点E , 连接AE , 使AE平分∠CAB .6. 如图,是由边长为1的小正方形构成的6×6网格,每个小正方形的顶点叫做格点,⊙O经过A、B、C、D四个格点,仅用无刻度的直尺在给定的网格中按要求画图(画图过程中起辅助作用的用虚线表示,画图结果用实线表示,并用黑色水笔描黑) (1)、如图1,判断圆心O(填“是”或“不是”)在格点上,并在图1中标出格点O;(2)、在图1中画出⊙O的切线CG(G为格点);(3)、在图2中画出的中点E;7. 如图,在的正方形网格中,每个小正方形的顶点叫做格点,经过格点 , 仅用无刻度的直尺在给定网格中画图.(保留作图痕迹)
(1)、如图1,判断圆心O(填“是”或“不是”)在格点上,并在图1中标出格点O;(2)、在图1中画出⊙O的切线CG(G为格点);(3)、在图2中画出的中点E;7. 如图,在的正方形网格中,每个小正方形的顶点叫做格点,经过格点 , 仅用无刻度的直尺在给定网格中画图.(保留作图痕迹)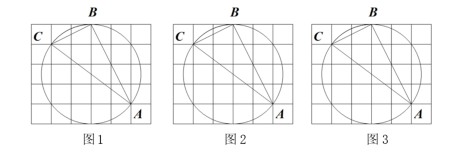 (1)、在图1中,画出的中线.(2)、在图2中,标出圆心 , 并画出的角平分线.(3)、在图3中,画出的边上的高线.8. 如图是的正方形网格,请仅用无刻度的直尺按要求完成以下作图(保留作图痕迹).
(1)、在图1中,画出的中线.(2)、在图2中,标出圆心 , 并画出的角平分线.(3)、在图3中,画出的边上的高线.8. 如图是的正方形网格,请仅用无刻度的直尺按要求完成以下作图(保留作图痕迹). (1)、在图1中作的角平分线;(2)、在图2中过点作一条直线,使点 , 到直线的距离相等.9. 如图在的网格中,的顶点都在格点上,仅用无刻度的直尺在给定的网格中分别按下列要求画图.(请保留画图痕迹,画图过程用虚线表示,画图结果用实线表示)
(1)、在图1中作的角平分线;(2)、在图2中过点作一条直线,使点 , 到直线的距离相等.9. 如图在的网格中,的顶点都在格点上,仅用无刻度的直尺在给定的网格中分别按下列要求画图.(请保留画图痕迹,画图过程用虚线表示,画图结果用实线表示) (1)、在图1中,画出的重心G;(2)、在图2中,画线段 , 点E在上,使得;(3)、图3中,在内寻找一格点N,使 , 并标注点N的位置.10. 如图,在6×6方格纸中,已知格点P和格点线段AC,请按要求画出以AC为对角线的格点四边形(顶点均在格点上),且点P在四边形内部(不包括边界上).
(1)、在图1中,画出的重心G;(2)、在图2中,画线段 , 点E在上,使得;(3)、图3中,在内寻找一格点N,使 , 并标注点N的位置.10. 如图,在6×6方格纸中,已知格点P和格点线段AC,请按要求画出以AC为对角线的格点四边形(顶点均在格点上),且点P在四边形内部(不包括边界上). (1)、在图1中画出一个▱ABCD;(2)、在图2中画出一个四边形AECF , 使得点P落在四边形某一边的中垂线上,且四边形中有且仅有两个内角为直角.11. 图①、图②均为4×4的正方形网格,每个小正方形的顶点称为格点,每个小正方形的边长均为1.线段AB、BC 的端点均在格点上,只用无刻度的直尺,在给定的网格中按要求作图,使所画图形的顶点均在格点上,所画图形不全等.
(1)、在图1中画出一个▱ABCD;(2)、在图2中画出一个四边形AECF , 使得点P落在四边形某一边的中垂线上,且四边形中有且仅有两个内角为直角.11. 图①、图②均为4×4的正方形网格,每个小正方形的顶点称为格点,每个小正方形的边长均为1.线段AB、BC 的端点均在格点上,只用无刻度的直尺,在给定的网格中按要求作图,使所画图形的顶点均在格点上,所画图形不全等. (1)、在图①中画一个四边形ABCD,∠ABC+∠DAB=180°;(2)、在图②中画一个四边形ABCE,使∠ABC=∠AEC;(3)、在图③中画一个四边形ABCF,使∠ABC+∠AFC=180°.12. 如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点(顶点是网格线的交点).
(1)、在图①中画一个四边形ABCD,∠ABC+∠DAB=180°;(2)、在图②中画一个四边形ABCE,使∠ABC=∠AEC;(3)、在图③中画一个四边形ABCF,使∠ABC+∠AFC=180°.12. 如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点(顶点是网格线的交点).
⑴以点为位似中心,在网格中画出 , 使与的位似比为;
⑵将向右平移7格,再向下平移2格,得到 , 画出;
⑶借助网格,在上选一点 , 使得平分的面积(保留确定关键点的画法),画出线段 .
13. 如图所示,在平面直角坐标系中△ABC三个顶点坐标分别为A(0,4),B(-4,1),C(2,0).
⑴作出△ABC关于x轴对称的△A1B1C1 , 并直接写出点B1的坐标 ▲ .
⑵在(1)的条件下,若点P在x轴上,当B1P+PA的值最小时,画出点P的位置,并直接写出B1P+PA的最小值.
⑶在x轴上是否存在一点M,使△MAC是等腰三角形,若存在,直接写出点M的坐标;若不存在,请说明理由.
14. 如图,为制作角度尺,将长为10,宽为4的矩形OABC分割成4×10的小正方形网格.在该矩形边上取点P,来表示∠POA的度数.阅读以下作图过程,并回答下列问题:作法(如图)
结论
①在上取点 , 使.
,
点表示.
②以为圆心,8为半径作弧,与交于点
,
点表示.
③分别以 , 为圆心,大于长度一半的长为半径作弧,相交于点E,F,连结EF与BC相交于点.
…
④以为圆心,的长为半径作弧,与射线交于点 , 连结交于点.
…
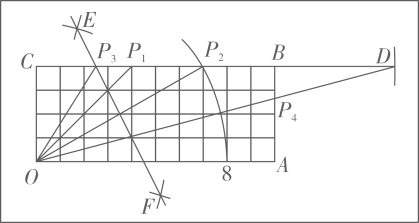 (1)、分别求点表示的度数.(2)、用直尺和圆规在该矩形的边上作点 , 使该点表示(保留作图痕迹,不写作法).15. 如图是由边长为的小正方形构成的网格.每个小正方形的顶点叫做格点.的顶点在格点上,仅用无刻度尺的直尺在给定网格中画图.画图过程用虚线表示.画图结果用实线表示,完成下列问题:
(1)、分别求点表示的度数.(2)、用直尺和圆规在该矩形的边上作点 , 使该点表示(保留作图痕迹,不写作法).15. 如图是由边长为的小正方形构成的网格.每个小正方形的顶点叫做格点.的顶点在格点上,仅用无刻度尺的直尺在给定网格中画图.画图过程用虚线表示.画图结果用实线表示,完成下列问题:
⑴ ▲ ;
⑶将边绕点顺时针旋转得到线段则 ▲ ;
⑶画出的外接圆的圆心;
⑷在上确定一点 , 使 .
16. 如图是由小正方形组成的12×11网格,每个小正方形的顶点叫作格点,过格点A,B,C的圆交于点F,点G在DE上,其中D,G是格点.仅用无刻度的直尺在给定网格中按要求完成画图,画图过程用虚线表示.
⑴在AD的下方画出正方形ADMN;
⑵画出圆心O;
⑶画出的中点P;
⑷画出线段AE绕点A逆时针旋转90°后的对应线段AQ.