2024年中考数学热点探究十一 与圆有关的辅助线
试卷更新日期:2024-04-27 类型:二轮复习
一、选择题(每题3分,共30分)
-
1. 如图,AB、BC为的两条弦,连接OA、OC,点D为AB的延长线上一点,若 , 则的度数为( )
 A、100° B、118° C、124° D、130°2. 如图,四边形ABCD内接于⊙O,AB为直径,∠C=120°,若AD=2,则AB的长为( )
A、100° B、118° C、124° D、130°2. 如图,四边形ABCD内接于⊙O,AB为直径,∠C=120°,若AD=2,则AB的长为( ) A、 B、2 C、2 D、43. 如图,AB为⊙O的直径,点C、D、E在⊙O上,且 , ∠E=70°,则∠ABC的度数为( )
A、 B、2 C、2 D、43. 如图,AB为⊙O的直径,点C、D、E在⊙O上,且 , ∠E=70°,则∠ABC的度数为( ) A、30° B、40° C、35° D、50°4. 如图,正六边形内接于 , 为上的一点(点不与点 , 重合),则的度数为( )
A、30° B、40° C、35° D、50°4. 如图,正六边形内接于 , 为上的一点(点不与点 , 重合),则的度数为( ) A、 B、 C、 D、5. 如图,是的直径,是的切线,为切点,的延长线交直线于点 , 连接 , 若 , , 则的长度是( )
A、 B、 C、 D、5. 如图,是的直径,是的切线,为切点,的延长线交直线于点 , 连接 , 若 , , 则的长度是( )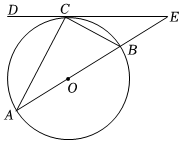 A、 B、 C、 D、6. 如图,是的直径, , 分别切于点、 , 若 , 则的度数是( )
A、 B、 C、 D、6. 如图,是的直径, , 分别切于点、 , 若 , 则的度数是( ) A、 B、 C、 D、7. 如图,半径长 , 点、、是三等分点,点为圆上一点,连接 , 且 , 交于点 , 则
A、 B、 C、 D、7. 如图,半径长 , 点、、是三等分点,点为圆上一点,连接 , 且 , 交于点 , 则 A、 B、 C、 D、8. 如图,在△ABC中,AB+AC=BC,AD⊥BC于D,⊙O为△ABC的内切圆,设⊙O的半径为R,AD的长为h,则的值为( )
A、 B、 C、 D、8. 如图,在△ABC中,AB+AC=BC,AD⊥BC于D,⊙O为△ABC的内切圆,设⊙O的半径为R,AD的长为h,则的值为( )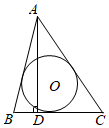 A、 B、 C、 D、9. 如图,AB为⊙O的直径,弦CD⊥AB于点F,OE⊥AC于点E,若OE=3,OB=5,则CD的长度是( )
A、 B、 C、 D、9. 如图,AB为⊙O的直径,弦CD⊥AB于点F,OE⊥AC于点E,若OE=3,OB=5,则CD的长度是( )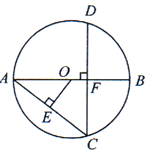 A、9.6 B、4 C、5 D、1010. 如图,点是的八等分点.若 , 四边形的周长分别为a,b,则下列正确的是( )
A、9.6 B、4 C、5 D、1010. 如图,点是的八等分点.若 , 四边形的周长分别为a,b,则下列正确的是( )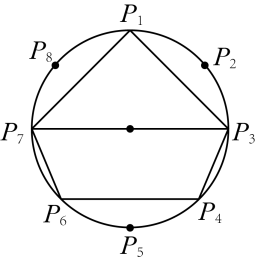 A、 B、 C、 D、a,b大小无法比较
A、 B、 C、 D、a,b大小无法比较二、填空题(每题4分,共20分)
-
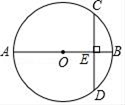
11. 如图,AB为⊙O的直径,弦CD⊥AB于点E,已知CD=6,EB=1,则⊙O的半径为 .
 12. 如图,是等边三角形的外接圆,其半径为4.过点B作于点E , 点P为线段上一动点(点P不与B , E重合),则的最小值为 .
12. 如图,是等边三角形的外接圆,其半径为4.过点B作于点E , 点P为线段上一动点(点P不与B , E重合),则的最小值为 .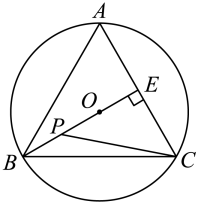 13. 如图,在⊙O中,AB切⊙O于点A,连接OB交⊙O于点C,过点A作AD∥OB交⊙O于点D,连接CD.若∠B=50°,则∠OCD的度数等于 .
13. 如图,在⊙O中,AB切⊙O于点A,连接OB交⊙O于点C,过点A作AD∥OB交⊙O于点D,连接CD.若∠B=50°,则∠OCD的度数等于 . 14. 如图,在平面直角坐标系中,点 , , 的坐标分别为 , , , 点是三角形的外接圆上一点,交线段于点 , 若 , 则点的坐标为.
14. 如图,在平面直角坐标系中,点 , , 的坐标分别为 , , , 点是三角形的外接圆上一点,交线段于点 , 若 , 则点的坐标为. 15. 如图,在等边三角形ABC中,点D,E分别是边BC,CA上的点,且BD=CE,连结AD,BE交于点P.连接CP,若CP⊥AP时,则AE:CE= ;设△ABC的面积为S1 , 四边形CDPE的面积为S2 , 则 = .
15. 如图,在等边三角形ABC中,点D,E分别是边BC,CA上的点,且BD=CE,连结AD,BE交于点P.连接CP,若CP⊥AP时,则AE:CE= ;设△ABC的面积为S1 , 四边形CDPE的面积为S2 , 则 = .
三、解答题(共5题,共42分)
-
16. 如图, , 是上的两点,是的直径,过点的切线交的延长线于点 , , 连接 , , .
 (1)、求证∶;(2)、若 , , 求的半径;(3)、在(2)的条件下,求出的面积.17. 如图,AB是⊙O的直径,AC是上半圆的弦,过点C作⊙O的切线DE交AB的延长线于点E , 且AD⊥DE于D , 与⊙O交于点F .
(1)、求证∶;(2)、若 , , 求的半径;(3)、在(2)的条件下,求出的面积.17. 如图,AB是⊙O的直径,AC是上半圆的弦,过点C作⊙O的切线DE交AB的延长线于点E , 且AD⊥DE于D , 与⊙O交于点F . (1)、判断AC是否是∠DAE的平分线?并说明理由;(2)、连接OF与AC交于点G , 当AG=GC=k时,求切线CE的长.18. 如图,在⊙O中,AB是弦,过点O作OA⊥OC与AB交于点C , 在OC的延长线取点D , 使DC=DB .
(1)、判断AC是否是∠DAE的平分线?并说明理由;(2)、连接OF与AC交于点G , 当AG=GC=k时,求切线CE的长.18. 如图,在⊙O中,AB是弦,过点O作OA⊥OC与AB交于点C , 在OC的延长线取点D , 使DC=DB .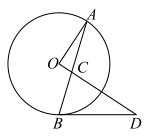 (1)、求证:BD是⊙O的切线;(2)、若BC=4, , 求⊙O的半径长.19. 如图, 与等边 的边 , 分别交于点 , , 是直径,过点 作 于点 .
(1)、求证:BD是⊙O的切线;(2)、若BC=4, , 求⊙O的半径长.19. 如图, 与等边 的边 , 分别交于点 , , 是直径,过点 作 于点 .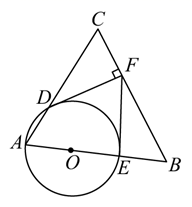 (1)、求证: 是 的切线;(2)、连接 ,当 是 的切线时,求 的半径 与等边 的边长 之间的数量关系.20. 如图,为的直径,弦于点E , 点F在上,连结并延长交与点G , 连结 , .
(1)、求证: 是 的切线;(2)、连接 ,当 是 的切线时,求 的半径 与等边 的边长 之间的数量关系.20. 如图,为的直径,弦于点E , 点F在上,连结并延长交与点G , 连结 , . (1)、如图1,求证:;(2)、如图2,与交于点N , 过点F作的平行线交于点M , 若 , 求 . (用含a的代数式表示)(3)、如图3,在(2)的条件下,连结 , 若与的面积相等,求的值.
(1)、如图1,求证:;(2)、如图2,与交于点N , 过点F作的平行线交于点M , 若 , 求 . (用含a的代数式表示)(3)、如图3,在(2)的条件下,连结 , 若与的面积相等,求的值.四、实践探究题(共3题,共28分)
-
21. 【概念呈现】在钝角三角形中,钝角的度数恰好是其中一个锐角的度数与90度的和,则称这个钝角三角形为和美三角形,这个锐角叫做和美角.
 (1)、【概念理解】当和美三角形是等腰三角形时,求和美角的度数.(2)、【性质探究】如图1,△ABC是和美三角形,∠B是钝角,∠A是和美角,
(1)、【概念理解】当和美三角形是等腰三角形时,求和美角的度数.(2)、【性质探究】如图1,△ABC是和美三角形,∠B是钝角,∠A是和美角,求证:.
(3)、【拓展应用】如图2,AB是⊙O的直径,且AB=13,点C,D是圆上的两点,弦CD与AB交于点E,连接AD,BD,△ACE是和美三角形.①当BC=5时,求AD的长.
②当△BCD是和美三角形时,直接写出的值.
22. 探究式学习是新课程倡导的重要学习方式,某兴趣小组拟做以下探究。如图1,等腰中, , 以为直径的与所在直线、分别交于点于点 .
 (1)、【初步感知】求证:为的切线;(2)、【深入研究】当时,若 , 求的长。(3)、【拓展延伸】如图2,当时,若 , 求的长。23. 定义:当点P在射线OA上时,把的值叫做点P在射线OA上的射影值;当点P不在射线OA上时,把射线OA上与点P最近点的射影值,叫做点P在射线OA上的射影值.
(1)、【初步感知】求证:为的切线;(2)、【深入研究】当时,若 , 求的长。(3)、【拓展延伸】如图2,当时,若 , 求的长。23. 定义:当点P在射线OA上时,把的值叫做点P在射线OA上的射影值;当点P不在射线OA上时,把射线OA上与点P最近点的射影值,叫做点P在射线OA上的射影值.例如:如图1,△OAB三个顶点均在格点上,BP是OA边上的高,则点P和点B在射线OA上的射影值均为 .
 (1)、在△OAB中,
(1)、在△OAB中,①点B在射线OA上的射影值小于1时,则△OAB是锐角三角形;
②点B在射线OA上的射影值等于1时,则△OAB是直角三角形;
③点B在射线OA上的射影值大于1时,则△OAB是钝角三角形.
其中真命题有 ▲ .
. ①② . ①③ . ②③ . ①②③
(2)、已知:点C是射线OA上一点,CA=OA=1,以〇为圆心,OA为半径画圆,点B是⊙O上任意点.①如图2,若点B在射线OA上的射影值为 . 求证:直线BC是⊙O的切线;
②如图3,已知D为线段BC的中点,设点D在射线OA上的射影值为x , 点D在射线OB上的射影值为y , 直接写出y与x之间的函数关系式为 .