2024年中考数学热点探究十一 与三角形、四边形有关的辅助线
试卷更新日期:2024-04-27 类型:二轮复习
一、选择题(每题3分,共24分)
-
1. 如图,在四边形 中,点P是边 上的动点,点Q是边 上的定点,连接 , 分别是 的中点,连接 .点P在由C到D运动过程中,线段EF的长度( )
 A、保持不变 B、逐渐变小 C、先变大,再变小 D、逐渐变大2. 如图,半径长 , 点、、是三等分点,点为圆上一点,连接 , 且 , 交于点 , 则
A、保持不变 B、逐渐变小 C、先变大,再变小 D、逐渐变大2. 如图,半径长 , 点、、是三等分点,点为圆上一点,连接 , 且 , 交于点 , 则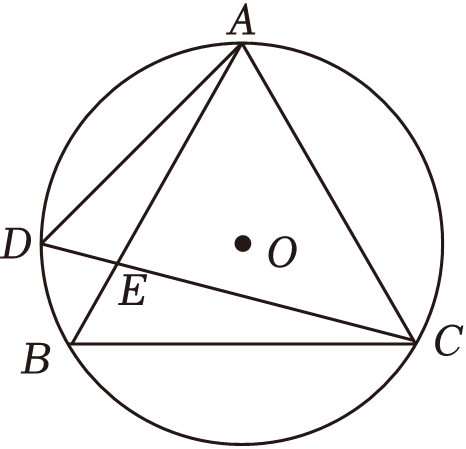 A、 B、 C、 D、3. 如图,矩形是由4块矩形拼接而成,矩形是由4个直角三角形和一个平行四边形拼接而成.则( )
A、 B、 C、 D、3. 如图,矩形是由4块矩形拼接而成,矩形是由4个直角三角形和一个平行四边形拼接而成.则( ) A、 B、 C、 D、4. 如图,在正方形中,点 , 分别在 , 上,且保持 , 在上取一点 , 连结 , 使恰好平分 , 连结 . 若要求正方形的面积,则只需要知道
A、 B、 C、 D、4. 如图,在正方形中,点 , 分别在 , 上,且保持 , 在上取一点 , 连结 , 使恰好平分 , 连结 . 若要求正方形的面积,则只需要知道 A、 的面积 B、 的面积 C、 的周长 D、 的周长5. 如图,在矩形ABCD中, , 点P是AD的中点,点E在BC上,CE=2BE,点M、N在线段BD上.若△PMN 是等腰三角形且底角与∠DEC相等,则MN的值为( )
A、 的面积 B、 的面积 C、 的周长 D、 的周长5. 如图,在矩形ABCD中, , 点P是AD的中点,点E在BC上,CE=2BE,点M、N在线段BD上.若△PMN 是等腰三角形且底角与∠DEC相等,则MN的值为( )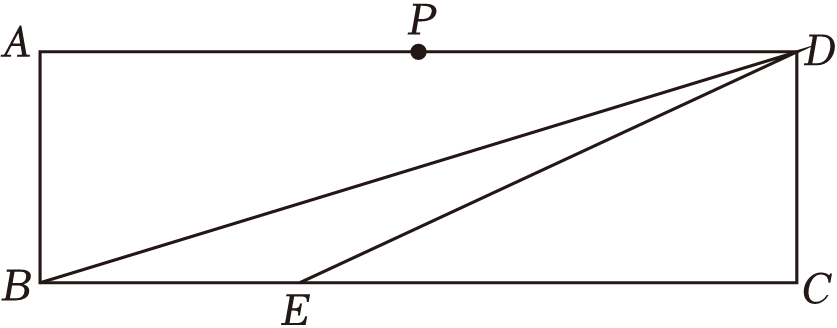 A、6或2 B、3或 C、2或3 D、6或6. 将四个全等的三角形按如图所示的方式围成一个正方形 , 记的面积为 , 四边形的面积为.若 , , , 则图中阴影部分的面积为( )
A、6或2 B、3或 C、2或3 D、6或6. 将四个全等的三角形按如图所示的方式围成一个正方形 , 记的面积为 , 四边形的面积为.若 , , , 则图中阴影部分的面积为( )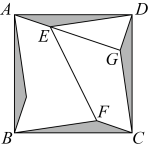 A、 B、 C、 D、7. 如图,在正方形中,是等边三角形, , 的延长线分别交于点 , , 连接 , ;与相交于点 . 给出下列结论:①;②;③;④;⑤ . 其中正确的结论有( )
A、 B、 C、 D、7. 如图,在正方形中,是等边三角形, , 的延长线分别交于点 , , 连接 , ;与相交于点 . 给出下列结论:①;②;③;④;⑤ . 其中正确的结论有( ) A、1个 B、2个 C、3个 D、4个8. 如图,AB是⊙O的直径,弦CD⊥AB于点E , 在BC上取点F , 使得CF=CE , 连结AF交CD于点G , 连结AD . 若CG=GF , 则的值等于( )
A、1个 B、2个 C、3个 D、4个8. 如图,AB是⊙O的直径,弦CD⊥AB于点E , 在BC上取点F , 使得CF=CE , 连结AF交CD于点G , 连结AD . 若CG=GF , 则的值等于( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每题4分,共20分)
-
9. 如图,是等边三角形的外接圆,其半径为4.过点B作于点E , 点P为线段上一动点(点P不与B , E重合),则的最小值为 .
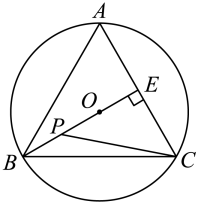 10. 如图,在平行四边形中, , , , 作对角线的垂直平分线 , 分别交对边、于点和点 , 则的长为 .
10. 如图,在平行四边形中, , , , 作对角线的垂直平分线 , 分别交对边、于点和点 , 则的长为 .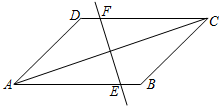 11. 如图,在中, , , , 平分 , 点F是的中点,点E是上的动点,则的最小值为 .
11. 如图,在中, , , , 平分 , 点F是的中点,点E是上的动点,则的最小值为 .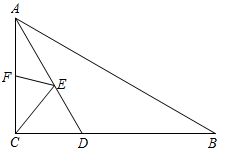 12. 如图,点E是边长为8的正方形ABCD的边AD上一动点(端点A , D除外),以CE为边作正方形CEFG , EF与AB交于点H , 连接BE , BF , BG . 下列四个结论:①BG=DE;②∠FAB=∠FEB;③当点E为AD中点时,H也是EF的中点;④当点E在AD边上运动时,AH有最大值为2.其中正确的结论是(填序号).
12. 如图,点E是边长为8的正方形ABCD的边AD上一动点(端点A , D除外),以CE为边作正方形CEFG , EF与AB交于点H , 连接BE , BF , BG . 下列四个结论:①BG=DE;②∠FAB=∠FEB;③当点E为AD中点时,H也是EF的中点;④当点E在AD边上运动时,AH有最大值为2.其中正确的结论是(填序号). 13. 如图,在等边三角形ABC中,点D,E分别是边BC,CA上的点,且BD=CE,连结AD,BE交于点P.连接CP,若CP⊥AP时,则AE:CE= ;设△ABC的面积为S1 , 四边形CDPE的面积为S2 , 则 = .
13. 如图,在等边三角形ABC中,点D,E分别是边BC,CA上的点,且BD=CE,连结AD,BE交于点P.连接CP,若CP⊥AP时,则AE:CE= ;设△ABC的面积为S1 , 四边形CDPE的面积为S2 , 则 = .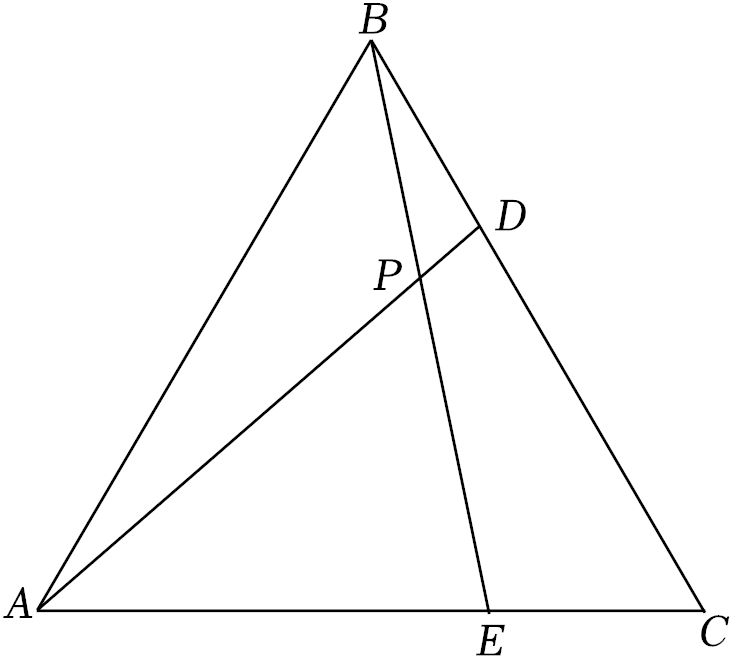
三、解答题(共4题,共36分)
-
14. 如图, 在平行四边形ABCD中, E为DC边的中点,连接AE, 若AE的延长线和BC的延长线相交于 F.
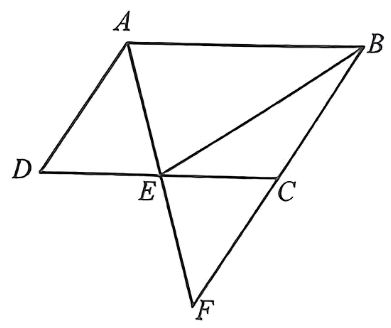 (1)、 求证: AD=FC;(2)、连接BE, 若△AEB的面积为2, 求平行四边形ABCD的面积.15. 如图1,已知四边形四条边上的中点分别为、、、、依次连接、、、、得到四边形 .
(1)、 求证: AD=FC;(2)、连接BE, 若△AEB的面积为2, 求平行四边形ABCD的面积.15. 如图1,已知四边形四条边上的中点分别为、、、、依次连接、、、、得到四边形 .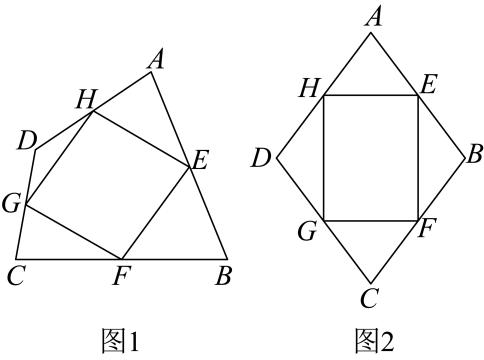 (1)、求证:四边形为平行四边形;(2)、连接与 , 当与满足什么条件时,四边形是矩形?(3)、如图2,若四边形是菱形,则四边形是什么图形,请说明理由.16. 如图,在一个正六边形中,点是该正六边形的中心,将该六边形的每条边延长,延长线的交点分别为、、、、、 .
(1)、求证:四边形为平行四边形;(2)、连接与 , 当与满足什么条件时,四边形是矩形?(3)、如图2,若四边形是菱形,则四边形是什么图形,请说明理由.16. 如图,在一个正六边形中,点是该正六边形的中心,将该六边形的每条边延长,延长线的交点分别为、、、、、 .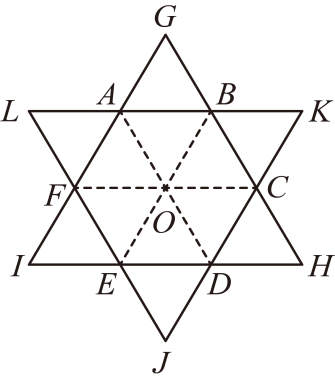 (1)、证明四边形是菱形;(2)、若的长为6,请计算正六边形的面积.17. 如图,在中, , . 点是延长线上一动点,连接 , 将绕点顺时针旋转得到 , 连接交于点 .
(1)、证明四边形是菱形;(2)、若的长为6,请计算正六边形的面积.17. 如图,在中, , . 点是延长线上一动点,连接 , 将绕点顺时针旋转得到 , 连接交于点 . (1)、求证:;(2)、如图1,若 , , , 求的大小;(3)、如图2,若点为中点, , , 求的长(用含的代数式表示).
(1)、求证:;(2)、如图1,若 , , , 求的大小;(3)、如图2,若点为中点, , , 求的长(用含的代数式表示).四、实践探究题(共4题,共40分)
-
18. 如图,已知四边形ABCD为正方形,AB=3 , 点E为对角线AC上一动点,连接DE,过点E作EF⊥DE,交BC于点F,以DE、EF为邻边作矩形DEFG,连接CG.
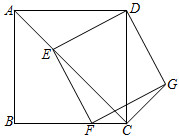 (1)、求证:矩形DEFG是正方形;(2)、探究:CE+CG的值是否为定值?若是,请求出这个定值;若不是,请说明理由.19. “转化”是解决数学问题的重要思想方法,通过构造图形全等或者相似建立数量关系是处理问题的重要手段.
(1)、求证:矩形DEFG是正方形;(2)、探究:CE+CG的值是否为定值?若是,请求出这个定值;若不是,请说明理由.19. “转化”是解决数学问题的重要思想方法,通过构造图形全等或者相似建立数量关系是处理问题的重要手段. (1)、【问题情景】:如图(1),正方形中,点是线段上一点(不与点、重合),连接.将绕点顺时针旋转90°得到 , 连接 , 求的度数.
(1)、【问题情景】:如图(1),正方形中,点是线段上一点(不与点、重合),连接.将绕点顺时针旋转90°得到 , 连接 , 求的度数.以下是两名同学通过不同的方法构造全等三角形来解决问题的思路,
①小聪:过点作的延长线的垂线;
②小明:在上截取 , 使得;
请你选择其中一名同学的解题思路,写出完整的解答过程.
(2)、【类比探究】:如图(2)点是菱形边上一点(不与点、重合), , 将绕点顺时针旋转得到 , 使得(),则的度数为(用含的代数式表示)(3)、【学以致用】:如图(3),在(2)的条件下,连结 , 与相交于点 , 当时,若 , 求的值.20. 综合与实践在△ABC中,AB=AC,D为边BC的中点,以D为顶点作∠MDN=∠B.
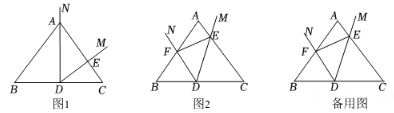 (1)、如图1,当射线DN经过点A时,DM交边AC于点E,不添加辅助线,则图①中与△ADE相似的三角形有.(填序号)
(1)、如图1,当射线DN经过点A时,DM交边AC于点E,不添加辅助线,则图①中与△ADE相似的三角形有.(填序号)①△ABD ②△ADC ③△ABC④△DCE
(2)、如图2,将∠MDN绕点D沿逆时针方向旋转,DM,DN分别交线段AC,AB于点E,F(点E与点A不重合),求证:△BDF∽△DEF(3)、在图2中,若AB=AC=5,BC=6,当△DEF的面积等于△ABC的面积时,求线段EF的长.21. 我们定义:有一组邻边相等且有一组对角互补的凸四边形叫做等补四边形. (1)、如图1,是等边三角形,在上任取一点D(B、C除外),连接 , 我们把绕点A逆时针旋转60°,则与重合,点D的对应点E.请根据给出的定义判断,四边形(选择是或不是)等补四边形.(2)、如图2,等补四边形中, , , 若 , 求的长.(3)、如图3,四边形中, , , , 求四边形面积的最大值.
(1)、如图1,是等边三角形,在上任取一点D(B、C除外),连接 , 我们把绕点A逆时针旋转60°,则与重合,点D的对应点E.请根据给出的定义判断,四边形(选择是或不是)等补四边形.(2)、如图2,等补四边形中, , , 若 , 求的长.(3)、如图3,四边形中, , , , 求四边形面积的最大值.