2024年中考数学热点探究七 以函数为背景的几何综合性问题
试卷更新日期:2024-04-27 类型:二轮复习
一、选择题(每题2分,共20分)
-
1. 如图,在平面直角坐标系中,平行四边形的边在轴的正半轴上, , 两点的坐标分别为 , , 点在第一象限,将直线沿轴向右平移个单位.若平移后的直线与边有交点,则的取值范围是( )
 A、 B、 C、 D、2. 如图, 为矩形 的对角线,已知 , .点P沿折线 以每秒1个单位长度的速度运动(运动到D点停止),过点P作 于点E,则 的面积y与点P运动的路程x间的函数图象大致是( )
A、 B、 C、 D、2. 如图, 为矩形 的对角线,已知 , .点P沿折线 以每秒1个单位长度的速度运动(运动到D点停止),过点P作 于点E,则 的面积y与点P运动的路程x间的函数图象大致是( ) A、
A、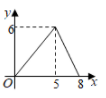 B、
B、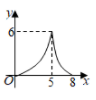 C、
C、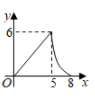 D、
D、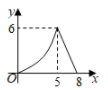 3. 如图,的半径是 , 点是直线上一动点,过点作的切线,切点为 , 连接 , , 则的最小值为( )
3. 如图,的半径是 , 点是直线上一动点,过点作的切线,切点为 , 连接 , , 则的最小值为( )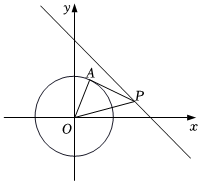 A、 B、 C、 D、4. 已知如图,反比例函数 , 的图象分别经过正方形、正方形的顶点D、A , 连接 , 则的面积等于( )
A、 B、 C、 D、4. 已知如图,反比例函数 , 的图象分别经过正方形、正方形的顶点D、A , 连接 , 则的面积等于( )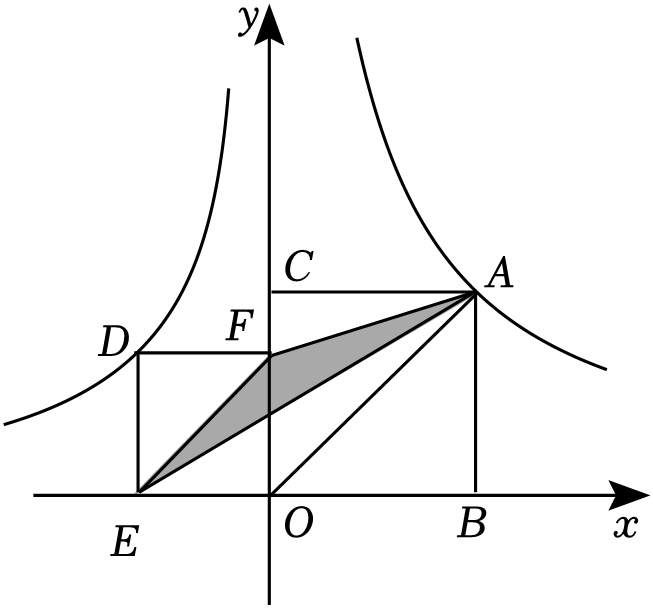 A、2 B、3 C、1 D、55. 如图 , 点、在反比例函数的图象上,过点、作轴的垂线,垂足分别为 , , 延长线段交轴于点 , 当时,阴影部分的面积;如图 , 点、在反比例函数的图象上,过点、作轴的垂线,垂足分别为 , , 连接 , 交于于点 , 当时,阴影部分的面积 , 则的值为( )
A、2 B、3 C、1 D、55. 如图 , 点、在反比例函数的图象上,过点、作轴的垂线,垂足分别为 , , 延长线段交轴于点 , 当时,阴影部分的面积;如图 , 点、在反比例函数的图象上,过点、作轴的垂线,垂足分别为 , , 连接 , 交于于点 , 当时,阴影部分的面积 , 则的值为( ) A、 B、 C、 D、6. 如图,等腰直角三角形ABC中,∠A=90°,BC=8,点D、点E分别是BC、AC边上的点,DE//AB则S△BDE的最大值是( )
A、 B、 C、 D、6. 如图,等腰直角三角形ABC中,∠A=90°,BC=8,点D、点E分别是BC、AC边上的点,DE//AB则S△BDE的最大值是( )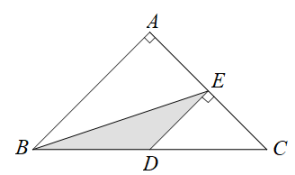 A、3 B、4 C、5 D、67. 如图, 正方形OABC有三个顶点在抛物线 上, 点 是原点, 顶点 在 轴上则顶点 的坐标是 ( )
A、3 B、4 C、5 D、67. 如图, 正方形OABC有三个顶点在抛物线 上, 点 是原点, 顶点 在 轴上则顶点 的坐标是 ( )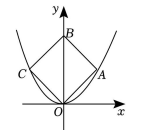 A、 B、 C、 D、8. 如图,在平面直角坐标系中,直线y=-3x+3交x轴于点A,交y轴于点B,以AB为边在第一象限作正方形ABCD,其中顶点D恰好落在双曲线y=k/x上,现将正方形ABCD沿y轴向下平移a个单位长度,可以使得顶点C落在双曲线上,则a的值为( )
A、 B、 C、 D、8. 如图,在平面直角坐标系中,直线y=-3x+3交x轴于点A,交y轴于点B,以AB为边在第一象限作正方形ABCD,其中顶点D恰好落在双曲线y=k/x上,现将正方形ABCD沿y轴向下平移a个单位长度,可以使得顶点C落在双曲线上,则a的值为( )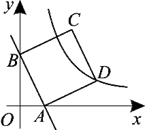 A、 B、 C、2 D、9. 如图,正方形ABCD边长为8,M,N分别是边BC,CD上的两个动点,且AM⊥MN,则AN的最小值是( )
A、 B、 C、2 D、9. 如图,正方形ABCD边长为8,M,N分别是边BC,CD上的两个动点,且AM⊥MN,则AN的最小值是( )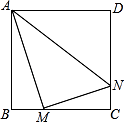 A、8 B、4 C、10 D、810. 如图,抛物线 (a>0)与x轴交于A,B,顶点为点D,把抛物线在x轴下方部分关于点B作中心对称,顶点对应D′,点A对应点C,连接DD′,CD′,DC,当△CDD′是直角三角形时,a的值为( )
A、8 B、4 C、10 D、810. 如图,抛物线 (a>0)与x轴交于A,B,顶点为点D,把抛物线在x轴下方部分关于点B作中心对称,顶点对应D′,点A对应点C,连接DD′,CD′,DC,当△CDD′是直角三角形时,a的值为( ) A、 或 B、 或 C、 或 D、 或
A、 或 B、 或 C、 或 D、 或二、填空题(每题2分,共10分)
-
11. 若直线:与轴、轴分别交于点和点 , 直线:与轴、轴分别交于点和点 , 线段与的中点分别是 , , 点为轴上一动点.
点的坐标为 ;
当的值最小时,点的坐标为 . 12. 如图,矩形ABCD中,AB=2cm,AD=5cm,动点P从点A出发,以1cm/s的速度沿AD向终点D移动,设移动时间为t(s).连接PC,以PC为一边作正方形PCEF,连接DE、DF,则△DEF面积最小值为 .
12. 如图,矩形ABCD中,AB=2cm,AD=5cm,动点P从点A出发,以1cm/s的速度沿AD向终点D移动,设移动时间为t(s).连接PC,以PC为一边作正方形PCEF,连接DE、DF,则△DEF面积最小值为 . 13. 如图,一次函数的图象交轴于点 , 交轴于点 , 点在射线上不与、重合 , 过点分别作轴和轴的垂线,垂足为、当矩形的面积为时,点的坐标为 .
13. 如图,一次函数的图象交轴于点 , 交轴于点 , 点在射线上不与、重合 , 过点分别作轴和轴的垂线,垂足为、当矩形的面积为时,点的坐标为 . 14. 如图,点A , B在反比例函数的图象上,点C , D在反比例函数的图象上,轴,已知点A , B的横坐标分别为2,4,与的面积之差为1,则k的值为 .
14. 如图,点A , B在反比例函数的图象上,点C , D在反比例函数的图象上,轴,已知点A , B的横坐标分别为2,4,与的面积之差为1,则k的值为 .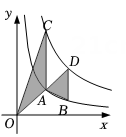 15. 如图,点E是边长为8的正方形ABCD的边AD上一动点(端点A , D除外),以CE为边作正方形CEFG , EF与AB交于点H , 连接BE , BF , BG . 下列四个结论:①BG=DE;②∠FAB=∠FEB;③当点E为AD中点时,H也是EF的中点;④当点E在AD边上运动时,AH有最大值为2.其中正确的结论是(填序号).
15. 如图,点E是边长为8的正方形ABCD的边AD上一动点(端点A , D除外),以CE为边作正方形CEFG , EF与AB交于点H , 连接BE , BF , BG . 下列四个结论:①BG=DE;②∠FAB=∠FEB;③当点E为AD中点时,H也是EF的中点;④当点E在AD边上运动时,AH有最大值为2.其中正确的结论是(填序号).
三、综合题(共4题,共33分)
-
16. 如图①,在矩形ABCD中,AB=6, AD=10,点E在边BC上,且BE=4,动点P从点E出发,沿折线EB-BA-AD以每秒2个单位长度的速度运动.作∠PEQ=90°,EQ交边AD或边DC于点Q,连接PQ.当点Q与点C重合时,点P停止运动、设点P的运动时间为t秒.(t>0)
 (1)、当点P和点B重合时,线段PQ的长为(2)、当点Q和点D重合时,求sin∠PQE;(3)、当点P在边AD上运动时, △PQE的形状始终是等腰直角三角形,如图②,请说明理由;(4)、作点E关于直线PQ的对称点F ,连接PF、QF ,当四边形EPFQ和矩形ABCD重叠部分图形为轴对称四边形时,直接写出t的取值范围.17. 如图①,一次函数的图象与轴交于点 , 点是反比例函数的图象与一次函数的图象在第一象限的交点.
(1)、当点P和点B重合时,线段PQ的长为(2)、当点Q和点D重合时,求sin∠PQE;(3)、当点P在边AD上运动时, △PQE的形状始终是等腰直角三角形,如图②,请说明理由;(4)、作点E关于直线PQ的对称点F ,连接PF、QF ,当四边形EPFQ和矩形ABCD重叠部分图形为轴对称四边形时,直接写出t的取值范围.17. 如图①,一次函数的图象与轴交于点 , 点是反比例函数的图象与一次函数的图象在第一象限的交点. (1)、求点B的坐标;(2)、点是反比例函数在第一象限内的图象上有别于的另外一点,过点作交轴于点 . 在轴正半轴上是否存在一点 , 使四边形是平行四边形,如果存在,请确定的长度,如果不存在,请说明理由.18. 如图,在等腰直角三角形ABC中,∠ACB=90°,AC=BC=4,D是AB的中点,E,F分别是AC,BC上的点(点E不与端点A,C重合),且AE=CF,连接EF并取EF的中点O,连接DO并延长至点G,使GO=OD,连接DE,DF,GE,GF.
(1)、求点B的坐标;(2)、点是反比例函数在第一象限内的图象上有别于的另外一点,过点作交轴于点 . 在轴正半轴上是否存在一点 , 使四边形是平行四边形,如果存在,请确定的长度,如果不存在,请说明理由.18. 如图,在等腰直角三角形ABC中,∠ACB=90°,AC=BC=4,D是AB的中点,E,F分别是AC,BC上的点(点E不与端点A,C重合),且AE=CF,连接EF并取EF的中点O,连接DO并延长至点G,使GO=OD,连接DE,DF,GE,GF.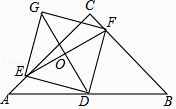 (1)、求证:四边形EDFG是正方形;(2)、当点E在什么位置时,四边形EDFG的面积最小?并求四边形EDFG面积的最小值.19. 如图,已知 , 是的平分线,是射线上一点, . 动点从点出发,以的速度沿水平向左作匀速运动,与此同时,动点从点出发,也以的速度沿竖直向上作匀速运动.连接 , 交于点 . 经过、、三点作圆,交于点 , 连接、 . 设运动时间为 , 其中 .
(1)、求证:四边形EDFG是正方形;(2)、当点E在什么位置时,四边形EDFG的面积最小?并求四边形EDFG面积的最小值.19. 如图,已知 , 是的平分线,是射线上一点, . 动点从点出发,以的速度沿水平向左作匀速运动,与此同时,动点从点出发,也以的速度沿竖直向上作匀速运动.连接 , 交于点 . 经过、、三点作圆,交于点 , 连接、 . 设运动时间为 , 其中 .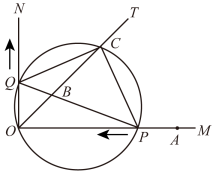 (1)、求的值;(2)、是否存在实数t , 使得线段的长度最大?若存在,求出t的值;若不存在,说明理由.(3)、在点P , 点Q运动过程中,四边形的面积是否发生改变,如果变,请说明理由;如果不变,请求出四边形的面积.
(1)、求的值;(2)、是否存在实数t , 使得线段的长度最大?若存在,求出t的值;若不存在,说明理由.(3)、在点P , 点Q运动过程中,四边形的面积是否发生改变,如果变,请说明理由;如果不变,请求出四边形的面积.四、实践探究题(共6题,共57分)
-
20. 综合与实践
如图1,某兴趣小组计划开垦一个面积为的矩形地块种植农作物,地块一边靠墙,另外三边用木栏围住,木栏总长为 .

【问题提出】
小组同学提出这样一个问题:若 , 能否围出矩形地块?
【问题探究】
小颖尝试从“函数图象”的角度解决这个问题:
设为 , 为 . 由矩形地块面积为 , 得到 , 满足条件的可看成是反比例函数的图象在第一象限内点的坐标;木栏总长为 , 得到 , 满足条件的可看成一次函数的图象在第一象限内点的坐标,同时满足这两个条件的就可以看成两个函数图象交点的坐标.
如图2,反比例函数的图象与直线:的交点坐标为和 ▲ , 因此,木栏总长为时,能围出矩形地块,分别为: , ;或 ▲ m , ▲ m .
 (1)、根据小颖的分析思路,完成上面的填空.(2)、【类比探究】
(1)、根据小颖的分析思路,完成上面的填空.(2)、【类比探究】若 , 能否围出矩形地块?请仿照小颖的方法,在图2中画出一次函数图象并说明理由.
(3)、【问题延伸】当木栏总长为时,小颖建立了一次函数 . 发现直线可以看成是直线通过平移得到的,在平移过程中,当过点时,直线与反比例函数的图象有唯一交点.
请在图2中画出直线过点时的图象,并求出的值.
(4)、【拓展应用】小颖从以上探究中发现“能否围成矩形地块问题”可以转化为“与图象在第一象限内交点的存在问题”.
若要围出满足条件的矩形地块,且和的长均不小于 , 请直接写出的取值范围.
21. (1)、【探究·发现】正方形的对角线长与它的周长及面积之间存在一定的数量关系.已知正方形的对角线长为a,则正方形的周长为 , 面积为(都用含a的代数式表示).(2)、【拓展·综合】如图1,若点M、N是某个正方形的两个对角顶点,则称M、N互为“正方形关联点”,这个正方形被称为M、N的“关联正方形”.
(1)、【探究·发现】正方形的对角线长与它的周长及面积之间存在一定的数量关系.已知正方形的对角线长为a,则正方形的周长为 , 面积为(都用含a的代数式表示).(2)、【拓展·综合】如图1,若点M、N是某个正方形的两个对角顶点,则称M、N互为“正方形关联点”,这个正方形被称为M、N的“关联正方形”.①在平面直角坐标系中,点P是原点O的“正方形关联点”.若 , 则O、P的“关联正方形”的周长是 ▲ ;若点P在直线上,则O、P的“关联正方形”面积的最小值是 ▲ .
②如图2,已知点 , 点B在直线上,正方形是A、B的“关联正方形”,顶点P、Q到直线l的距离分别记为a和b,求的最小值.
22. 如图,在平面直角坐标系中,点 , 为的顶点, , 点C在x轴上.将沿x轴水平向右平移a个单位得到 , A , B两点的对应点 , 恰好落在反比例函数的图象上. (1)、求a和k的值;(2)、作直线l平行于且与 , 分别交于M , N , 若与四边形的面积比为 , 求直线l的函数表达式;(3)、在(2)问的条件下,是否存在x轴上的点P和直线l上的点Q , 使得以P , Q , , 四个点为顶点的四边形是平行四边形?若存在,请直接写出符合题意的点P , Q的坐标;若不存在,请说明理由.23. 综合与实践
(1)、求a和k的值;(2)、作直线l平行于且与 , 分别交于M , N , 若与四边形的面积比为 , 求直线l的函数表达式;(3)、在(2)问的条件下,是否存在x轴上的点P和直线l上的点Q , 使得以P , Q , , 四个点为顶点的四边形是平行四边形?若存在,请直接写出符合题意的点P , Q的坐标;若不存在,请说明理由.23. 综合与实践【问题提出】
某兴趣小组开展综合实践活动:在中, , 为上一点, , 动点以每秒1个单位的速度从点出发,在三角形边上沿匀速运动,到达点时停止,以为边作正方形.设点的运动时间为 , 正方形的面积为 , 探究与的关系.
 (1)、【初步感知】如图1,当点由点运动到点时,
(1)、【初步感知】如图1,当点由点运动到点时,①当时,;
②关于的函数解析式为.
(2)、当点由点运动到点时,经探究发现是关于的二次函数,并绘制成如图2所示的图象.请根据图象信息,求关于的函数解析式及线段的长.(3)、【延伸探究】若存在3个时刻 , , 对应的正方形的面积均相等.①▲;
②当时,求正方形的面积.
24. 定义:对角线互相垂直且相等的四边形叫做垂等四边形.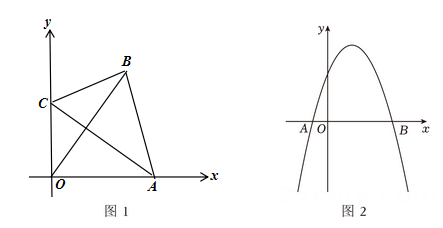 (1)、理解应用:如图,在平面直角坐标系xOy中,已知四边形OABC是垂等四边形,点A的坐标为(4,0),点C的坐标为(0,3),则点B的坐标为 .(2)、综合探究:如图,已知抛物线y=﹣x2+2x+3与x轴交于A,B两点,点A在点B的左侧,C,D两点在该抛物线上.若以A,B,C,D为顶点的四边形是垂等四边形.设点C的横坐标为m,点D的横坐标为n,且m>n,求m的值.25. 用一条直线截三角形的两边,若所截得的四边形对角互补,则称该直线为三角形第三条边上的逆平行线.如图1,DE为△ABC的截线,截得四边形BCED , 若∠BDE+∠C=180°,则称DE为△ABC边BC的逆平行线.
(1)、理解应用:如图,在平面直角坐标系xOy中,已知四边形OABC是垂等四边形,点A的坐标为(4,0),点C的坐标为(0,3),则点B的坐标为 .(2)、综合探究:如图,已知抛物线y=﹣x2+2x+3与x轴交于A,B两点,点A在点B的左侧,C,D两点在该抛物线上.若以A,B,C,D为顶点的四边形是垂等四边形.设点C的横坐标为m,点D的横坐标为n,且m>n,求m的值.25. 用一条直线截三角形的两边,若所截得的四边形对角互补,则称该直线为三角形第三条边上的逆平行线.如图1,DE为△ABC的截线,截得四边形BCED , 若∠BDE+∠C=180°,则称DE为△ABC边BC的逆平行线.
如图2,已知△ABC中,AB=AC , 过边AB上的点D作DE∥BC交AC于点E , 过点E作边AB的逆平行线EF , 交边BC于点F .
(1)、求证:DE是边BC的逆平行线.(2)、点O是△ABC的外心,连接CO . 求证:CO⊥FE .(3)、已知AB=5,BC=6,过点F作边AC的逆平行线FG , 交边AB于点G .①试探索AD为何值时,四边形AGFE的面积最大,并求出最大值;
②在①的条件下,比较AD+BG ▲ AB大小关系.(“<、>或=”)