2024年中考数学热点探究六函数应用型问题

试卷更新日期：2024-04-27 类型：二轮复习

进入出卷网下载

一、选择题（每题2分，共20分）

1. 某烤鸭店在确定烤鸭的烤制时间时，主要依据的是表中的数据：
鸭的质量/千克
0.5
1
1.5
2
2.5
3
3.5
4
烤制时间/分钟
40
60
80
100
120
140
160
180
设鸭的质量为x千克，烤制时间为t ．估计当x＝3.8千克时，t的值约为（）

A、140 B、160 C、170 D、180

查看试题解析
2. 一种弹簧秤最大能称不超过10kg的物体，不挂物体时弹簧的长为12cm，每挂重1kg物体，弹簧伸长0.5cm.在弹性限度内，挂重后弹簧的长度y（cm）与所挂物体的质量x（kg）之间的函数表达式为（）

A、 $y = 12 - 0.5 x$ B、 $y = 12 + 0.5 x$ C、 $y = 10 + 0.5 x$ D、 $y = 0.5 x$

查看试题解析
3. 下面的三个问题中都有两个变量：
$①$ 京沪铁路全程为 $1463 k m$ ，某次列车的平均速度 $y ($ 单位： $k m / h)$ 与此次列车的全程运行时间 $x ($ 单位： $h)$ ；
$②$ 已知北京市的总面积为 $1.68 \times 1 0^{4} k m^{2}$ ，人均占有面积 $y ($ 单位： $k m^{2} /$ 人 $)$ 与全市总人口 $x ($ 单位：人 $)$ ；
$③$ 某油箱容量是 $50 L$ 的汽车，加满汽油后开了 $200 k m$ 时，油箱中汽油大约消耗了 $\frac{1}{4} .$ 油箱中的剩油量 $y L$ 与加满汽油后汽车行驶的路程 $x k m$ ．
其中，变量 $y$ 与变量 $x$ 之间的函数关系可以用如图所示的图象表示的是（）

A、 $① ②$ B、 $① ③$ C、 $② ③$ D、 $① ② ③$

查看试题解析
4. 古希腊著名的科学家阿基米德发现了杠杆平衡，后来人们把它归纳为“杠杆原理”，即“阻力 $\times$ 阻力臂 $=$ 动力 $\times$ 动力臂” $.$ 小明同学用撬棍撬动一块大石头，已知阻力和阻力臂分别是 $1200 N$ 和 $0.5 m$ ，则动力 $F ($ 单位： $N)$ 关于动力臂 $l ($ 单位： $m)$ 的函数表达式正确的是（）

A、 $F = \frac{1200}{l}$ B、 $F = \frac{600}{l}$ C、 $F = \frac{1000}{l}$ D、 $F = \frac{2400}{l}$

查看试题解析
5. 在四个密闭容器中分别装有甲、乙、丙、丁四种气体，如图，用四个点分别描述这四种气体的密度 $ρ (k g / m^{2})$ 与体积 $V (m^{2})$ 的情况，其中描述乙、丁两种气体情况的点恰好在同一个反比例函数的阁象上，则这四种气体的质量最小的是（）

A、甲 B、乙 C、丙 D、丁

查看试题解析
6. 某综合实践活动小组设计了简易电子体重秤：制作一个装有踏板（踏板质量忽略不计）的可变电阻 $R_{1} (Ω)$ （如图 1），当人站上踏板时，通过电压表显示的读数 $U_{0}$ 换算为人的质量 $m (k g$ ），已知 $U_{0}$ 随着 $R_{1}$ 的变化而变化（如图 2）， $R_{1}$ 与踏板上人的质量 $m$ 的关系见图3. 则下列说法不正确的是（）

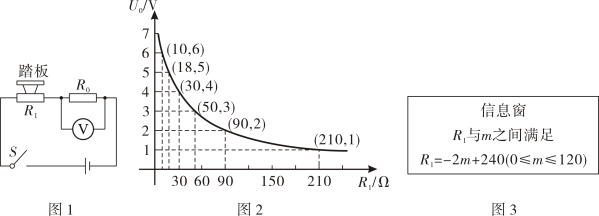A、在一定范围内， $U_{0}$ 越大， $R_{1}$ 越小 B、当 $U_{0} = 3 V$ 时， $R_{1}$ 的阻值为 $50 Ω$ C、当踏板上人的质量为 $90 k g$ 时， $U_{0} = 2 V$ D、若电压表量程为 $0 ~ 6 V (0 \leq U_{0} \leq 6)$ ，为保护电压表，该电子体重科可称的最大质量是 $115 k g$

查看试题解析
7. 某农场拟建两间矩形饲养室，一面靠现有墙 $($ 墙足够长 $)$ ，中间用一道墙隔开，并在如图所示的三处各留 $1 m$ 宽的门，已知计划中的材料可建墙体 $($ 不包括门 $)$ 总长为 $27 m$ ，则能建成的饲养室的总面积最大为（）

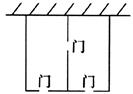A、 $75 m^{2}$ B、 $\frac{75}{2} m^{2}$ C、 $48 m^{2}$ D、 $\frac{225}{2} m^{2}$

查看试题解析
8. 某商品现在的售价为每件60元，每星期可卖出300件．市场调查反映，如果调整商品售价，每降价1元，每星期可多卖出20件．设每件商品降价x元后，每星期售出商品的总销售额为y元，则y与x的关系式为（）

A、 $y = 60 (300 + 20 x)$ B、 $y = (60 - x) (300 + 20 x)$ C、 $y = 300 (60 - 20 x)$ D、 $y = (60 - x) (300 - 20 x)$

查看试题解析
9. 如图1是莲花山景区一座抛物线形拱桥，按图2所示建立平面直角坐标系，得到抛物线解析式为y＝ $- \frac{1}{36} x^{2}$ ，正常水位时水面宽AB为36m，当水位上升5m时水面宽CD为（）

A、10m B、12m C、24m D、48m

查看试题解析
10. 如图1，一个移动喷灌架喷射出的水流可以近似地看成抛物线.图2是喷灌架为一坡地草坪喷水的平面示意图，喷水头的高度（喷水头距喷灌架底部的距离）是1米.当喷射出的水流距离喷水头20米时，达到最大高度11米，现将喷灌架置于坡度为1∶10的坡地底部点O处，草坡上距离О的水平距离为30米处有一棵高度约为2.3米的石榴树AB，因为刚刚被喷洒了农药，近期不能被喷灌.下列说法正确的是（）

A、水流运行轨迹满足函数 $y = - \frac{1}{40} x^{2} - x + 1$ B、水流喷射的最远水平距离是40米 C、喷射出的水流与坡面OA之间的最大铅直高度是9.1米 D、若将喷灌架向后移动7米，可以避开对这棵石榴树的喷灌

查看试题解析

二、填空题（每题2分，共10分）

11. 声音在空气中的传播速度

v (m / s)

与温度

t (℃)

的关系如表：

温度 $(℃)$	$0$	$5$	$10$	$15$	$20$
速度 $v (m / s)$	$331$	$336$	$341$	$346$	$351$

则速度 $v$ 与温度 $t$ 之间的关系式为；当 $t = 30 ℃$ 时，声音的传播速度为 $m / s$ ．

查看试题解析

12. 杆秤是我国传统的计重工具，如图，可以用秤砣到秤纽的水平距离，来得出秤钩上所挂物体的质量．称重时，若秤砣到秤纽的水平距离为x（单位：cm）时，秤钩所挂物重为y（单位：kg），则y是x的一次函数．下表记录了四次称重的数据，其中只有一组数据记录错误，它是第组．

组数	1	2	3	4
x/cm	1	2	4	7
y/kg	0.60	0.85	1.45	2.10

查看试题解析

13. 饮水机中原有水的温度为 $20 ℃$ ，通电开机后，饮水机自动开始加热(此过程中，水温 $y ℃$ 与开机时间 $x$ 分满足一次函数关系)，当加热到 $100 ℃$ 时自动停止加热，随后水温开始下降(此过程中，水温 $y ℃$ 与开机时间x分成反比例函数关系)，当水温降至 $20 ℃$ 时，饮水机又自动开始加热，……如此循环下去(如图所示)．那么开机后 $56$ 分钟时，水的温度是 $℃$ ．

查看试题解析
14. 漏刻是我国古代的一种计时工具．据史书记载，西周时期就已经出现了漏刻，这是中国古代人民对函数思想的创造性应用．小明同学依据漏刻的原理制作了一个简单的漏刻计时工具模型，研究中发现水位 $h (c m)$ 是时间 $t (m i n)$ 的一次函数，下表是小明记录的部分数据，其中有一个 $h$ 的值记录错误，请排除后利用正确的数据确定当 $h$ 为 $8 c m$ 时，对应的时间 $t$ 为 $m i n$ ．
          $t (m i n)$
…
1
2
3
5
…
          $h (c m)$
…
2.4
2.8
3.4
4
…

查看试题解析
15. 小明和小强做弹球游戏，如图1，小明向斜坡找一个乒乓球，乒乓球弹起的运行路线是一条抛物线，乒乓球落地后又弹起，第二次弹起的运行路线和第一次运行路线的抛物线形状相同．小强在地面立一块高度为 $0.4 m$ 的木板，以斜坡底端 $O$ 为坐标原点，地面水平线为 $x$ 轴，取单位长度为 $1 m$ ，建立如图2所示的平面直角坐标系，乒乓球的大小忽略不计，经测量发现，拋球点 $A$ 的坐标为 $(- 1 ， 3.36)$ ，第一次弹起的运行路线最高点坐标为 $(- 0.5 ， 3.61)$ ，第二次弹起的最大高度为 $1.21 m$ ．

(1)、求乒乓球第一次落地点B距斜坡低端O的距离是 $m$ ；

(2)、为了确保乒乓球在第二次下落时能落在木板上，小强将木板立在到斜坡底端O的最小距离是 $m$ ．

查看试题解析

三、解答题（共7题，共55分）

16. 科学课上，同学用自制密度计测量液体的密度．密度计悬浮在不同的液体中时，浸在液体中的高度h（单位：cm）是液体的密度 $ρ$ （单位： $g / c m^{3}$ ）的反比例函数，当密度计悬浮在密度为 $1 g / c m^{3}$ 的水中时， $h = 20 c m$ ．

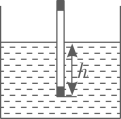(1)、求h关于 $ρ$ 的函数解析式．

(2)、当密度计悬浮在另一种液体中时， $h = 25 c m$ ，求该液体的密度 $ρ$ ．

查看试题解析
17. 网络直播带货已成为一种新业态，某网店尝试用60天的时间，按单价随天数而变化的直播带货模式销售一种成本为10元/每件的商品，经过统计得到此商品的日销售量 $m$ （件）、销售单价 $n$ （元/件）在第 $x$ 天（x为正整数）销售的相关信息：
① $m$ 与 $x$ 满足一次函数关系，且第1天的日销售量为98件，第4天的日销售量为92件；
② $n$ 与 $x$ 函数关系如下图所示；

(1)、第5天的日销售量件； $n$ 与 $x$ 的函数关系式为．

(2)、在这60天中，网店哪天销售该商品的日利润 $y$ 最大？最大是多少元？

(3)、在这60天中，共有多少天日利润 $y$ 不低于2418元？

查看试题解析
18. 学校与图书馆在同一条笔直道路上，甲从学校去图书馆，乙从图书馆回学校，甲、乙两人都匀速步行且同时出发，乙先到达目的地．两人之间的距离y（米）与时间t（分钟）之间的函数关系如图所示．

(1)、根据图象信息，求出甲和乙的速度各为多少？（单位：米/分钟）

(2)、求线段AB所在的直线的函数表达式；

(3)、在整个过程中，请通过计算，t为何值时两人相距400米？

查看试题解析
19. 电子体重秤度数直观又便于携带，为人们带来了方便，某综合实践活动小组设计了简易电子体重秤：一个装有踏板（踏板质量忽略不计）的可变电阻 $R_{1}$ 与踏板上人的质量 $m$ 之间的函数关系式为 $R_{1} = k m + b$ （其中 $k$ ， $b$ 为常数， $0 \leq m \leq 120$ ），其图象如图①所示；图②的电路中，电源电压恒为8伏，定值电阻 $R_{0}$ 的阻值为30欧，接通开关，人站上踏板，电压表显示的度数为 $U_{0}$ ，该度数可以换算为人的质量 $m$ .
注：①导体两端的电压 $U$ ，导体的电阻 $R$ ，通过导体的电流 $I$ ，满足关系式 $I = \frac{U}{R}$ .
②串联电路中电流处处相等，各电阻两端的电压之和等于总电压，即：可变电阻 $R_{1}$ 两端的电压+定值电阻 $R_{0}$ 两端的电压=总电压.

(1)、求出 $R_{1}$ 关于 $m$ 的函数解析式；

(2)、当 $U_{0} = 1.5$ 伏时， $R_{1} =$ 欧；

(3)、若电压表量程为0-6伏，为保护电压表，请求出该电子体重秤可称的最大质量.

查看试题解析
20. 小明和小亮在做传球训练，某同学借做此情境编了一道数学题．
在如图的平面直角坐标系中，一个单位长度代表1m，小明从点A(8，2)处将球传出，其运动路线为抛物线 $C_{1} : y = a (x - 4)^{2} + 4$ 的一部分，小亮在 B处接住球，然后跳起将球传出，球的运动路线是抛物线 $C_{2} : y = - \frac{1}{10} x^{2} + \frac{n}{10} x + \frac{5}{2}$ 的一部分．

(1)、求抛物线C₁的函数表达式；

(2)、设抛物线C₁的顶点为点 M，在x轴上找一点P，求使| $| P A - P M |$ 的值最大的点P的坐标；

(3)、若小明在x轴上方2m的高度上，且到点A水平距离不超过1m的范围内可以接到球，求符合条件的n的整数值．

查看试题解析
21. 如图1为某公园的圆形喷水池，小玲学习了二次函数后，受到该图启发设计了一种新的喷水池，它的截面示意图如图2所示， $O$ 为水池中心，喷头 $A$ 、 $B$ 之间的距离为 $18$ 米，喷射水柱呈抛物线形，水柱距水池中心 $6 m$ 处达到最高，高度为 $4 m$ ．水池中心处有一个圆柱形蓄水池，其高 $C F$ 为 $1.75$ 米．

(1)、在图2中，以点 $O$ 为坐标原点，水平方向为 $x$ 轴建立直角坐标系，并求右边这条抛物线的函数解析式．

(2)、如图3，拟在圆柱形蓄水池中心处建一喷水装置 $O P (O P ⊥ C D)$ ，从点 $P$ 向四周喷射抛物线形水柱且满足以下四个条件：不能碰到图2中的水柱；落水点 $H$ ， $N$ 的间距为 $H N = 0.5 m$ ；水柱的最高点与点 $P$ 的高度差为 $1 m$ ；从点 $P$ 向四周喷射与图2中形状相同的抛物线形水柱．
①在建立的坐标系中，求落水点 $H$ 的坐标；
②求出喷水装置 $O P$ 的高度．

查看试题解析
22. 麻城市思源实验学校自从开展“高效课堂”模式以来，在课堂上进行当堂检测效果很好．每节课40分钟教学，假设老师用于精讲的时间x（单位：分钟）与学生学习收益量y的关系如图1所示，学生用于当堂检测的时间x（单位：分钟）与学生学习收益y的关系如图2所示（其中OA是抛物线的一部分，A为抛物线的顶点），且用于当堂检测的时间不超过用于精讲的时间．

(1)、求老师精讲时的学生学习收益量y与用于精讲的时间x之间的函数关系式；

(2)、求学生当堂检测的学习收益量y与用于当堂检测的时间x的函数关系式；

(3)、问此“高效课堂”模式如何分配精讲和当堂检测的时间，才能使学生在这40分钟的学习收益总量最大？

查看试题解析

四、实践探究题（共4题，共35分）

23. 根据以下素材，探索完成任务．

如何确定木板分配方案？
素材1	我校开展爱心义卖活动，小艺和同学们打算推销自己的手工制品．他们以每块15元的价格买了100张长方形木板，每块木板长和宽分别为80cm，40cm.
素材2	现将部分木板按图1虚线裁剪，剪去四个边长相同的小正方形（阴影）．把剩余五个矩形拼制成无盖长方体收纳盒，使其底面长与宽之比为3：1．其余木板按图2虚线裁剪出两块木板（阴影是余料），给部分盒子配上盖子．
素材3	义卖时的售价如标签所示：
问题解决
任务1	计算盒子高度	求出长方体收纳盒的高度．
任务2	确定分配方案1	若制成的有盖收纳盒个数大于无盖收纳盒，但不到无盖收纳盒个数的2倍，木板该如何分配？请给出分配方案．
任务3	确定分配方案2	为了提高利润，小艺打算把图2裁剪下来的余料（阴影部分）利用起来，一张矩形余料可以制成一把小木剑，并以5元/个的价格销售．请确定木板分配方案，使销售后获得最大利润．

查看试题解析

24. 阅读与思考

下面是小宇同学的一篇日记，请仔细阅读并完成相应的任务.

在物理活动课上，我们“博学”小组的同学，参加了一次“探究电功率 $P$ 与电阻 $R$ 之间的函数关系”的活动.

第一步，实验测量.根据物理知识，改变电阻 $R$ 的大小，通过测量电路中的电流，计算电功率 $P$ .

第二步，整理数据.

R/Ω	…	3	6	9	12	15	…
P/W	…	3	1.5	1	0.75	0.7	…

第三步，描点连线，以 $R$ 的数值为横坐标，对应 $P$ 的数值为纵坐标在平面直角坐标系中描出以表中数值为坐标的各点，并用光滑的曲线顺次连接这些点.

在数据分析时，我发现一个数据有错误，重新测量计算后，证明了我的猜想正确，并修改了表中这个数据.实验结束后，大家都有很多收获，每人都撰写了日记.

任务：

(1)、表格中错误的数据是，

P

与

R

的函数表达式为；

(2)、在平面直角坐标系中，画出

P

与

R

的函数图象；

(3)、结合图象，直接写出P大于6W时R的取值范围.

查看试题解析

25. 根据以下素材，探索完成任务．

如何设计跳长绳方案
素材1	图1是集体跳长绳比赛，比赛时，各队跳绳10人，摇绳2人，共计12人．图2是绳甩到最高处时的示意图，可以近似的看作一条抛物线，正在甩绳的甲、乙两位队员拿绳的手间距6米，到地面的距离均为1米，绳子最高点距离地面2.5米．
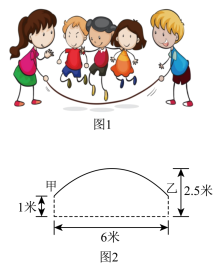
素材2	某队跳绳成员有6名男生和4名女生，男生身高1.70米至1.80米，女生身高1.66米至1.68米．跳长绳比赛时，可以采用一路纵队或两路纵队并排的方式安排队员位置，但为了保证安全，人与人之间距离至少0.5米．
问题解决
任务1	确定长绳形状	在图2中建立合适的直角坐标系，并求出抛物线的函数表达式．
任务2	探究站队方式	当该队以一路纵队的方式跳绳时，绳子能否顺利的甩过所有队员的头顶？
任务3	拟定位置方案	为了更顺利的完成跳绳，现按中间高两边低的方式居中安排站位．请在你所建立的坐标系中，求出左边第一位跳绳队员横坐标的最大取值范围．

查看试题解析

26. 根据下列素材，完成相应任务

仓储品装容的优化设计
素材1	如图1是某个仓库，图2是其横截面的示意图，已知墙体OA=2.6米，BC=5米，水平距离OC=12米，其顶部的轮廓为抛物线的一部分，建立如图所示的平面直角坐标系后它可以近似地用函数 y= $- \frac{1}{15}$ x²+bx+c表示
素材2	图3是棱长为1m的立方体仓储品，将四件一样的仓储品如图4所示叠放在MN处，MN=1m.当叉车要取货物时，需要将其向上抬升10cm，沿水平方向移动1米后取出。
素材3	如图5，为保证能够用叉车安全顺利地搬运和放置仓储品进出仓库，需设计三条宽度为2米的过道OE，HC，FG，以及在过道之间设计两块宽度不少于2米的仓储区域EF，GH. 要求： ①靠近过道的仓储品需从就近过道搬运，其余可从左或右搬运。 ②尽可能多的装容仓储品.
问题解决
任务1	确定顶部形状	求仓库离地的最大距离.
任务2	确定摆放高度	当OM=2.4米时，试分别判断叉车能否从左边或右边取出?请说明理由。
任务3	设计最优方案	已知该仓库的长为50米，请你根据素材和要求设计：仓储区EF= ▲米， GH= ▲米，仓库最大仓储品容量为 ▲件.

查看试题解析

鸭的质量/千克	0.5	1	1.5	2	2.5	3	3.5	4
烤制时间/分钟	40	60	80	100	120	140	160	180

$t (m i n)$	…	1	2	3	5	…
$h (c m)$	…	2.4	2.8	3.4	4	…

2024年中考数学热点探究六 函数应用型问题

一、选择题（每题2分，共20分）

二、填空题（每题2分，共10分）

三、解答题（共7题，共55分）

四、实践探究题（共4题，共35分）

2024年中考数学热点探究六函数应用型问题