2024年中考数学热点探究五 一次函数与反比例函数结合问题
试卷更新日期:2024-04-27 类型:二轮复习
一、选择题(每题3分,共30分)
-
1. 反比例函数的图象与一次函数的图象交于A、B两点,其中 , 当时,x的取值范围是( )A、 B、 C、 D、或2. 如图,直线与双曲线交于点和点 , 则不等式的解集是( )
 A、 B、 C、或 D、或3. 如图所示,反比例函数y=(x<0)与一次函数 y=x+4的图象交于A,B两点,A,B两点的横坐标分别为-3,-1.则关于x的不等式<x+4(x<0)的解集为( )
A、 B、 C、或 D、或3. 如图所示,反比例函数y=(x<0)与一次函数 y=x+4的图象交于A,B两点,A,B两点的横坐标分别为-3,-1.则关于x的不等式<x+4(x<0)的解集为( ) A、x<-3 B、-3<x<-1 C、-1<x<0 D、x<-3或-1<x<04. 如图,直线y=x+2与反比例函的图像在第一象限交于点P . 若 , 则k的值为( )
A、x<-3 B、-3<x<-1 C、-1<x<0 D、x<-3或-1<x<04. 如图,直线y=x+2与反比例函的图像在第一象限交于点P . 若 , 则k的值为( )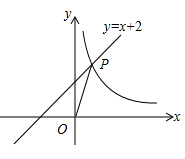 A、6 B、8 C、10 D、125. 如图,直线与双曲线交于两点,点在轴上,连接 , 且 , 已知的面积为 , 则的值为( )
A、6 B、8 C、10 D、125. 如图,直线与双曲线交于两点,点在轴上,连接 , 且 , 已知的面积为 , 则的值为( ) A、 B、 C、 D、6. 如图,直线与双曲线交于A、B两点,其横坐标分别为1和5,则不等式的解为( )
A、 B、 C、 D、6. 如图,直线与双曲线交于A、B两点,其横坐标分别为1和5,则不等式的解为( )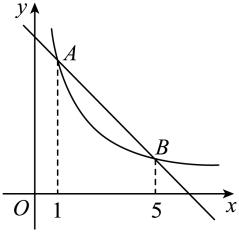 A、 B、或 C、或 D、或7. 正比例函数y=x与反比例函数y=的图象相交于A , C两点,AB⊥x轴于点B , CD⊥x轴于点D(如图),则四边形ABCD的面积为( )
A、 B、或 C、或 D、或7. 正比例函数y=x与反比例函数y=的图象相交于A , C两点,AB⊥x轴于点B , CD⊥x轴于点D(如图),则四边形ABCD的面积为( ) A、1 B、2 C、4 D、88. 如图,直线与双曲线交于两点,轴于点 , 连接交轴于点。下列结论:①;②的面积为定值;③是的中点;④ . 其中正确的结论有( )
A、1 B、2 C、4 D、88. 如图,直线与双曲线交于两点,轴于点 , 连接交轴于点。下列结论:①;②的面积为定值;③是的中点;④ . 其中正确的结论有( )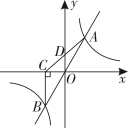 A、1个 B、2个 C、3个 D、4个9. 已知在平面直角坐标系中,正比例函数y=k1x(k1>0)的图象与反比例函数(k2>0)的图象的两个交点中,有一个交点的横坐标为1,点A(t , p)和点B(t+2,q)在函数y=k1x的图象上(t≠0且t≠-2),点C(t , m)和点D(t+2,n)在函数的图象上.当p-m与q-n的积为负数时,t的取值范围是( )A、或 B、或 C、-3<t<-2或-1<t<0 D、-3<t<-2或0<t<110. 如图,在直角坐标系中,直线与坐标轴交于、两点,与双曲线交于点 , 过点作轴,垂足为 , 且 , 则以下结论:
A、1个 B、2个 C、3个 D、4个9. 已知在平面直角坐标系中,正比例函数y=k1x(k1>0)的图象与反比例函数(k2>0)的图象的两个交点中,有一个交点的横坐标为1,点A(t , p)和点B(t+2,q)在函数y=k1x的图象上(t≠0且t≠-2),点C(t , m)和点D(t+2,n)在函数的图象上.当p-m与q-n的积为负数时,t的取值范围是( )A、或 B、或 C、-3<t<-2或-1<t<0 D、-3<t<-2或0<t<110. 如图,在直角坐标系中,直线与坐标轴交于、两点,与双曲线交于点 , 过点作轴,垂足为 , 且 , 则以下结论:
;
当时,;
如图,当时,;
当时,随的增大而增大,随的增大而减小.
其中正确结论的个数是 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每题3分,共15分)
-
11. 如图,经过原点的直线交反比例函数的y=图象于A , B两点,过点A作AC⊥x轴于点C , 连接BC , 当S△ABC=2时,k的值为 .
 12. 如图,在平面直角坐标系中,O是坐标原点,直线向下平移b个单位后与反比例函数交第一象限于点A , 交x轴于B点, , , 则 .
12. 如图,在平面直角坐标系中,O是坐标原点,直线向下平移b个单位后与反比例函数交第一象限于点A , 交x轴于B点, , , 则 .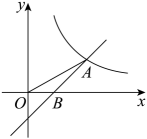 13. 如图,正比例函数的图象与反比例函数的图象交于、两点.点在轴负半轴上, , 的面积为12,则 .
13. 如图,正比例函数的图象与反比例函数的图象交于、两点.点在轴负半轴上, , 的面积为12,则 . 14. 如图所示,直线y=kx(k>0)与双曲线y=交于A(x1 , y1),B(x2 , y2)两点,则2x1y2-7x2y1的值等于。
14. 如图所示,直线y=kx(k>0)与双曲线y=交于A(x1 , y1),B(x2 , y2)两点,则2x1y2-7x2y1的值等于。 15. 直线y=-x+2a(常数)和双曲线的图象有且只有一个交点B,一次函数y=-x+2a与x轴交于点A,点P是线段OA上的动点,点Q在反比例函数图象上,且满足∠BPO=∠QPA.设PQ与线段AB的交点为M,若OM⊥BP,则的值为 .
15. 直线y=-x+2a(常数)和双曲线的图象有且只有一个交点B,一次函数y=-x+2a与x轴交于点A,点P是线段OA上的动点,点Q在反比例函数图象上,且满足∠BPO=∠QPA.设PQ与线段AB的交点为M,若OM⊥BP,则的值为 .
三、解答题(共6题,共44分)
-
16. 如图,B,C是反比例函数y= (k≠0)在第一象限图象上的点,过点B的直线y=x-1与x轴交于点A,CD⊥x轴,垂足为D,CD与AB交于点E,OA=AD,CD=3.
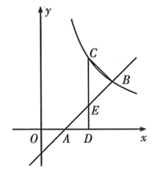 (1)、求此反比例函数的表达式;(2)、求△BCE的面积.17. 如图在平面直角坐标系中,一次函数y=kx+b的图象经过点A(0,﹣4)、B(2,0)交反比例函数的图象于点C(3,a),点P在反比例函数的图象上,横坐标为n(0<n<3),PQ∥y轴交直线AB于点Q , 连接OP、OQ .
(1)、求此反比例函数的表达式;(2)、求△BCE的面积.17. 如图在平面直角坐标系中,一次函数y=kx+b的图象经过点A(0,﹣4)、B(2,0)交反比例函数的图象于点C(3,a),点P在反比例函数的图象上,横坐标为n(0<n<3),PQ∥y轴交直线AB于点Q , 连接OP、OQ . (1)、求一次函数和反比例函数的表达式;(2)、求△OPQ面积的最大值.18. 如图,已知直线l:y=x+4与反比例函数的图象交于点A(﹣1,n),直线l'经过点A , 且与l关于直线x=﹣1对称.
(1)、求一次函数和反比例函数的表达式;(2)、求△OPQ面积的最大值.18. 如图,已知直线l:y=x+4与反比例函数的图象交于点A(﹣1,n),直线l'经过点A , 且与l关于直线x=﹣1对称. (1)、求反比例函数的解析式;(2)、求图中阴影部分的面积;(3)、已知直线l:y=x+4与反比例函数的图象交于点另一点B , P在平面内,若以点A , B , P , O为顶点的四边形是平行四边形,请直接写出所有符合条件点P的坐标.19. 如图,一次函数的图象与x轴交于点 , 与y轴交于点 , 与反比例函数的图象交于点C , B是的中点.
(1)、求反比例函数的解析式;(2)、求图中阴影部分的面积;(3)、已知直线l:y=x+4与反比例函数的图象交于点另一点B , P在平面内,若以点A , B , P , O为顶点的四边形是平行四边形,请直接写出所有符合条件点P的坐标.19. 如图,一次函数的图象与x轴交于点 , 与y轴交于点 , 与反比例函数的图象交于点C , B是的中点.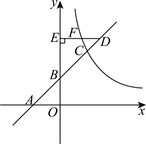 (1)、求一次函数和反比例函数的解析式;(2)、点D在一次函数的图象上且横坐标为3,过点D作轴于点E , 交反比例函数的图象于点F , 连 , 求四边形的面积.20. 如图,在同一平面直角坐标系中,一次函数的图象与反比例函数的图象交于、两点,与轴交于点 , 与轴交于点 , 连接 , 已知 , .
(1)、求一次函数和反比例函数的解析式;(2)、点D在一次函数的图象上且横坐标为3,过点D作轴于点E , 交反比例函数的图象于点F , 连 , 求四边形的面积.20. 如图,在同一平面直角坐标系中,一次函数的图象与反比例函数的图象交于、两点,与轴交于点 , 与轴交于点 , 连接 , 已知 , .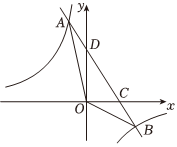 (1)、求反比例函数的解析式;(2)、直接写出时对应自变量的取值范围;(3)、若点在线段上,且 , 求点的坐标.21. 在平面直角坐标系xOy 中,直线与反比例函数的图象交于A(3,m),B两点.
(1)、求反比例函数的解析式;(2)、直接写出时对应自变量的取值范围;(3)、若点在线段上,且 , 求点的坐标.21. 在平面直角坐标系xOy 中,直线与反比例函数的图象交于A(3,m),B两点. (1)、求直线AB的函数表达式及点B的坐标;(2)、如图1,过点A的直线分别与x轴,反比例函数y=的图象(x<0)交于点M , N , 且 , 连接BM , 求△ABM的面积;(3)、如图2,点D在另一条反比例函数的图象上,点C在x轴正半轴上,连接DC交该反比例函数图象于点E , 且DE=2EC , 再连接AD , BC , 若此时四边形ABCD恰好为平行四边形,求k的值.
(1)、求直线AB的函数表达式及点B的坐标;(2)、如图1,过点A的直线分别与x轴,反比例函数y=的图象(x<0)交于点M , N , 且 , 连接BM , 求△ABM的面积;(3)、如图2,点D在另一条反比例函数的图象上,点C在x轴正半轴上,连接DC交该反比例函数图象于点E , 且DE=2EC , 再连接AD , BC , 若此时四边形ABCD恰好为平行四边形,求k的值.四、实践探究题(共3题,共31分)
-
22. 探究函数性质时,我们经历了列表、描点、连线画函数图象,观察分析图象特征,概括函数性质的过程.以下是我们研究函数性质及其应用的部分过程,请按要求完成下列各小题.
0
1
2
3
4
5
6
5
4
2
1
7
(1)、写出函数关系式中及表格中 , 的值:, , ;
(2)、根据表格中的数据在所给的平面直角坐标系中画出该函数的图象,并根据图象写出该函数的一条性质: ;(3)、已知函数的图象如图所示,结合你所画的函数图象,直接写出不等式的解集. 23. 模具厂计划生产面积为4,周长为的矩形模具,对于的取值范围,小亮已经能用“代数”的方法解决,现在他又尝试从“图形”的角度进行探究,过程如下:
23. 模具厂计划生产面积为4,周长为的矩形模具,对于的取值范围,小亮已经能用“代数”的方法解决,现在他又尝试从“图形”的角度进行探究,过程如下: (1)、建立函数模型:
(1)、建立函数模型:设矩形相邻两边的长分别为 , 由矩形的面积为4,得 , 即;由周长为 , 得 , 即 . 满足要求的应是两个函数图象在第象限内的交点的坐标.
(2)、画出函数图象:函数的图像如图所示,而函数的图像可由直线平移得到.请在同一直角坐标系中直接画出直线 .
(3)、平移直线 , 观察函数图象:当直线平移到与函数的图像有唯一交点时,写出周长的值;
(4)、得出结论:若能生产出面积为4的矩形模具,求出周长的取值范围 . (直接写出结论)
24. 综合与实践如图1,某兴趣小组计划开垦一个面积为的矩形地块种植农作物,地块一边靠墙,另外三边用木栏围住,木栏总长为 .

【问题提出】
小组同学提出这样一个问题:若 , 能否围出矩形地块?
【问题探究】
小颖尝试从“函数图象”的角度解决这个问题:
设为 , 为 . 由矩形地块面积为 , 得到 , 满足条件的可看成是反比例函数的图象在第一象限内点的坐标;木栏总长为 , 得到 , 满足条件的可看成一次函数的图象在第一象限内点的坐标,同时满足这两个条件的就可以看成两个函数图象交点的坐标.
如图2,反比例函数的图象与直线:的交点坐标为和 ▲ , 因此,木栏总长为时,能围出矩形地块,分别为: , ;或 ▲ m , ▲ m .
 (1)、根据小颖的分析思路,完成上面的填空.(2)、【类比探究】
(1)、根据小颖的分析思路,完成上面的填空.(2)、【类比探究】若 , 能否围出矩形地块?请仿照小颖的方法,在图2中画出一次函数图象并说明理由.
(3)、【问题延伸】当木栏总长为时,小颖建立了一次函数 . 发现直线可以看成是直线通过平移得到的,在平移过程中,当过点时,直线与反比例函数的图象有唯一交点.
请在图2中画出直线过点时的图象,并求出的值.
(4)、【拓展应用】小颖从以上探究中发现“能否围成矩形地块问题”可以转化为“与图象在第一象限内交点的存在问题”.
若要围出满足条件的矩形地块,且和的长均不小于 , 请直接写出的取值范围.