2024年中考数学热点探究三 含字母参数的方程(组)、不等式(组)
试卷更新日期:2024-04-27 类型:二轮复习
一、选择题(每题3分,共24分)
-
1. 已知 , 与 , 都是方程的解,则k与b的值分别是( )A、 , 4 B、 , 4 C、 , D、 ,2. 若关于x的方程 有正数解,则( ).A、m>0且m≠3 B、m<6且m≠3 C、m<0 D、m>63. 关于x的不等式组恰好有3个整数解,则a满足( )A、a=10 B、10≤a<12 C、10<a≤12 D、10≤a≤124. 已知关于x的方程(a , b , m均为常数,且)的两个解是 , 则方程的解是( )A、 B、 C、 D、5. 已知关于 , 的方程组 ,将此方程组的两个方程左右两边分别对应相加,得到一个新的方程,当 每取一个值时,就有一个方程,这些方程有一个公共解,这个公共解是( )A、 B、 C、 D、6. 在关于的二元一次方程组的下列说法中,正确的是( )
①当时,方程的两根互为相反数:
②当且仅当时,解得与相等;
③满足关系式;
④若 , 则 .
A、①③ B、①② C、①②③ D、①②③④7. 对实数x , y定义一种新的运算F , 规定若关于正数x的不等式组恰好有 3 个整数解,则m的取值范围是( )A、 B、 C、 D、8. 已知多项式 , 下列说法正确的个数为( )若 , 则代数式的值为; 当时,代数式的最小值为; 当时,若 , 则的取值范围是 .
A、个 B、个 C、个 D、个二、填空题(每题3分,共15分)
-
9. 若关于的方程无解,求的值 .10. 若关于x , y的方程组的解是 , 则关于m , n的方程组的解是 .11. 若关于x的不等式组有且只有四个整数解,且关于y的分式方程的解为非正数,则符合条件的所有整数a的和为 .12. 已知关于x的分式方程的解为整数,且关于y的不等式组有且仅有3个整数解,则所有满足条件的整数m的值之和是 .13. 对于实数m,n,先定义一种运算“⊗”如下: , 若x⊗(﹣2)=10,则实数x的值为 .
三、解答题(共5题,共43分)
-
14. 已知关于x、y的二元一次方程组 , 它的解是正数.(1)、求m的取值范围;(2)、化简: .15. 下图是一个运算程序:
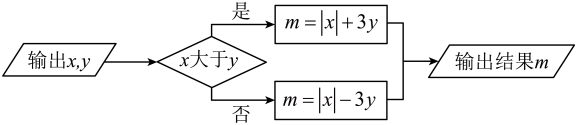 (1)、若 , , 求的值;(2)、若 , 输出结果的值是输入的值的两倍,求的值.16. 已知关于的一元二次方程 .(1)、求证:无论取任何实数,方程总有实数根;(2)、若一元二次方程的两根为 , , 且满足 , 求的值.17. 若.(1)、若以a、b、c为边的三角形,判断这个三角形的形状:(2)、解方程;(3)、若一元二次方程有实数根,求m的取值范围.18. 已知反比例函数的图像经过点 .
(1)、若 , , 求的值;(2)、若 , 输出结果的值是输入的值的两倍,求的值.16. 已知关于的一元二次方程 .(1)、求证:无论取任何实数,方程总有实数根;(2)、若一元二次方程的两根为 , , 且满足 , 求的值.17. 若.(1)、若以a、b、c为边的三角形,判断这个三角形的形状:(2)、解方程;(3)、若一元二次方程有实数根,求m的取值范围.18. 已知反比例函数的图像经过点 . (1)、求的值;(2)、完成下面的解答过程.
(1)、求的值;(2)、完成下面的解答过程.解不等式组
解:解不等式①,得;
在方格中画出反比例函数的大致图像,根据图像写出不等式②的解集是;
把不等式①和②的解集在数轴上表示出来;

从图中可以找出这两个不等式解集的公共部分,得到原不等式组的解集是 .
四、实践探究题(共4题,共38分)
-
19. 定义:若 , 是方程的两个整数根,且满足 , 则称此类方程为“差1方程”.例如:是“差方程”.(1)、下列方程是“差方程”的是;(填序号)
① ② ③;
(2)、若方程是“差方程”,求的值.20. 定义:如果关于x的一元二次方程ax2+bx+c=0(a≠0)满足b=a+c,那么我们称这个方程为“完美方程”.(1)、下面方程是“完美方程”的是 . (填序号)①x2-4x+3=0;②2x2+x+3=0;③2x2-x-3=0.(2)、已知3x2+mx+n=0是关于x的“完美方程”,若m是此“完美方程”的一个根,求m的值.21. 如果关于x的一元二次方程ax2+bx+c=0(a≠0)有两个实数根,且其中一个根为另一个根的2倍,那么称这样的方程为“倍根方程”.例如,一元二次方程x2-6x+8=0的两个根是x1=2和x2=4,则方程x2-6x+8=0是“倍根方程”.(1)、根据上述定义,一元二次方程2x2+x-1=0(填“是”或“不是”)“倍根方程”.(2)、若一元二次方程x2-3x+c=0是“倍根方程”,则c= .(3)、若关于x的一元二次方程ax2+bx+c=0(a≠0)是“倍根方程”,则a、b、c之间的关系为 .(4)、若(x-2)(mx-n)=0(m≠0)是“倍根方程”,求代数式4m2-5mn+n2的值.22. 定义新运算“”:对于实数 , , , , 有 , 其中等式的右边是通常的加法和乘法运算.例如: .(1)、求关于的方程的根;(2)、若关于的方程有两个实数根,求的取值范围.