2024年中考数学热点探究二整体思想在求值中的运用

试卷更新日期：2024-04-27 类型：二轮复习

进入出卷网下载

一、选择题（每题3分，共30分）

1. 已知x-y=4， xy=5，则 $x^{2} y - x y^{2}$ 的值为（）

A、25 B、20 C、15 D、10

查看试题解析
2. 如果代数式 $2 y^{2} - y$ 的值是 $7$ ，那么代数式 $4 y^{2} - 2 y + 1$ 的值等于（）

A、 $2$ B、 $3$ C、 $- 2$ D、 $15$

查看试题解析
3. 若 $a$ 是关于 $x$ 的方程 $3 x^{2} - x + 1 = 0$ 的一个根，则 $2022 - 6 a^{2} + 2 a$ 的值是（）

A、2024 B、2023 C、2022 D、2021

查看试题解析
4. 已知a是方程 $x^{2} - 2020 x + 4 = 0$ 的一个解，则 $a^{2} - 2019 a + \frac{8080}{a^{2} + 4} + 7$ 的值为（）

A、2023 B、2022 C、2021 D、2020

查看试题解析
5. 若 $n$ 为正整数．且 $a^{2 n} = 4$ ，则 ${(2 a^{3 n})}^{2} - 4 {(a^{2})}^{2 n}$ 的值为（）

A、4 B、16 C、64 D、192

查看试题解析
6. 若x、y二者满足等式 $x^{2} - 3 y = 3 x + y^{2}$ ，且x、y互为倒数，则代数式 $x^{2} - 3 (x + y) + 5 - y^{2} - 4 x y$ 的值为（）

A、1 B、4 C、5 D、9

查看试题解析
7. 若 $3 x^{2} + 4 x + 1 = 0$ ，则代数式 $6 x^{2} + 8 x + 2024$ 的值是（）

A、2021 B、2022 C、2023 D、2024

查看试题解析
8. 若m，n互为相反数，p，q互为倒数，t的绝对值等于4，则 ${(\frac{m + n}{200})}^{2022} - {(- p q)}^{2023} + t^{3}$ 的值是（）

A、 $- 63$ B、65 C、 $- 63$ 或65 D、63或 $- 65$

查看试题解析
9. 已知m为方程 $x^{2} + 3 x - 2024 = 0$ 的根，那么 $m^{3} + 2 m^{2} - 2027 m + 2024$ 的值为（）

A、-2024 B、0 C、2024 D、4048

查看试题解析
10. 已知一列数的和 $x_{1} + x_{2} + ⋯ + x_{2023} = \frac{1}{2} \times (1 + 2 + ⋯ + 2023)$ ，且 $x_{1} - 3 x_{2} + 1 = x_{2} - 3 x_{3} + 2 = ⋯ = x_{2022} - 3 x_{2023} + 2022 = x_{2023} - 3 x_{1} + 2023$ ，则 $x_{1} - 2 x_{2} - 3 x_{3}$ 的值是（）

A、2 B、 $- 2$ C、3 D、 $- 3$

查看试题解析

二、填空题（每题3分，共15分）

11. 若 $a^{2} + a - 5 = 0$ ，代数式 $(a^{2} - 5) (a + 1)$ 的值为．

查看试题解析
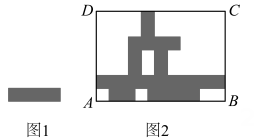
12. 已知 $a - b = \sqrt{2}$ ， $a - c = 2$ ，则代数式 ${(b - c)}^{2} + (b - c) + 4 =$ ．

查看试题解析
13. 给等式中的某些字母赋予一定的特殊值，可以解决一些问题．比如对于等式 ${(x + 3)}^{2} = a x^{2} + b x + c$ ，当 $x = 0$ 时，可得 $3^{2} = c$ ，计算得 $c = 9$ ；请你再给x赋不同的值，可计算得 $4 a + 2 b =$ ．

查看试题解析
14. 图1，由两个相同的小长方形组成的图形周长为10，图2中在长方形ABCD内放置了若干个相同的小长方形，则长方形ABCD的周长为.

查看试题解析
15. “整体思想”是中学数学解题中一种重要的思想方法，它在多项式的化简与求值中应用极为广泛．已知 $x = 2$ 是方程 $a - b x = 4$ 的解，则 $- 4 b + 2 a + 2027$ 的值为．

查看试题解析

三、解答题（共9题，共75分）

16. 已知：数a与b互为相反数，c与d互为倒数， $x = \pm 2$ ．求式子 ${(a + b)}^{2011} - \frac{{(a + b - c d)}^{2020}}{| x |}$ 的值．

查看试题解析
17. 先阅读下列材料，再解答问题：
材料：因式分解：(x+y)²+2(x+y)+1.
解：将“x+y”看成整体，令x+y=A，则原式=A²+2A+1=(A+1)².
再将“A”还原，得原式=(x+y+1)².
上述解题用到的是“整体思想”，“整体思想”是数学解题中常用的一种思想方法，请解答下列问题：

(1)、因式分解：1+2(2x-3y)+(2x-3y)²；

(2)、因式分解：(a+b)(a+b-4)+4.

查看试题解析
18. 整体代换是数学的一种思想方法，例如：已知 $x^{2} + x = 0$ ，求 $x^{2} + x + 1186$ 的值，我们将 $x^{2} + x$ 作为一个整体代入，则原式 $= 0 + 1186 = 1186$ ．仿照上面的解题方法，完成下面的问题：

(1)、如果 $a + b = 6$ ，求 $2 (a + b) - 4 a - 4 b + 2$ 的值；

(2)、若 $a^{2} + 2 a b = 20 ， b^{2} + 2 a b = 8$ ，求 $2 a^{2} - 4 b^{2} - 4 a b$ 的值．

查看试题解析
19. 阅读材料：我们知道，4x-2x+x=(4-2+1)x=3x，类似地，我们把(a+b)看成一个整体，则4(a+b)-2(a+b)+(a+b)=(4-2+1)(a+b)=3(a+b).“整体思想”是中学学习中的一种重要的思想方法，它在多项式的化简与求值中应用极为广泛.
尝试应用：

(1)、把(a-b)²看成一个整体，合并3(a-b)²-6(a-b)²+2(a-b)²的结果是；

(2)、已知x²-2y=4，求3x²-6y-21的值；

(3)、拓展探索：
已知a-2b=3，2b-c=-5，c-d=10，求(a-c)+(2b-d)-(2b-c)的值.

查看试题解析
20. 换元法是数学中的一种解题方法．若我们把其中某些部分看成一个整体，用一个新字母代替（即换元），则能使复杂的问题简单化．如：解二元一次方程组 ${\begin{array}{l} 2 (x + y) + 3 (x - y) = - 2 \\ x + y - 2 (x - y) = 3 \end{array}$ ，按常规思路解方程组计算量较大．可设 $x + y = a$ ， $x - y = b$ ，那么方程组可化为 ${\begin{array}{l} 2 a + 3 b = - 2 \\ a - 2 b = 3 \end{array}$ ，从而将方程组简单化，解出 $a$ 和 $b$ 的值后，再利用 $x + y = a$ ， $x - y = b$ 解出 $x$ 和 $y$ 的值即可．用上面的思想方法解方程：

(1)、 $\frac{x^{2}}{x + 2} + \frac{2 x + 4}{x^{2}} = 3$ ；

(2)、 $x^{2} + 2 x + 4 \sqrt{x^{2} + 2 x} - 5 = 0$

查看试题解析
21. 阅读材料：
解方程： ${(x^{2} - 1)}^{2} - 5 (x^{2} - 1) + 4 = 0$ ．我们可以将 $x^{2} - 1$ 视为一个整体，然后设 $x^{2} - 1 = y$ ，则 ${(x^{2} - 1)}^{2} = y^{2}$ ，原方程化为 $y^{2} - 5 y + 4 = 0$ ①，解得 $y_{1} = 1 ， y_{2} = 4$ ．
当 $y = 1$ 时， $x^{2} - 1 = 1 ， ∴ x^{2} = 2 ， ∴ x = \pm \sqrt{2}$ ．
当 $y = 4$ 时， $x^{2} - 1 = 4 ， ∴ x^{2} = 5 ， ∴ x = \pm \sqrt{5}$ ．
$∴$ 原方程的解为 $x_{1} = \sqrt{2} ， x_{2} = - \sqrt{2} ， x_{3} = \sqrt{5} ， x_{4} = - \sqrt{5}$ ．
根据上面的解答，解决下面的问题：

(1)、填空：在由原方程得到方程①的过程中，利用法达到降次的目的，体现了的数学思想；

(2)、解方程； $x^{4} - x^{2} - 12 = 0$ ．

查看试题解析
22. 阅读理解，并解决问题：
“整体思想”是中学数学中的一种重要思想，贯穿于中学数学的全过程，比如整体代入，整体换元，整体约减，整体求和，整体构造，…，有些问题若从局部求解，采取各个击破的方式，很难解决，而从全局着眼，整体思考，会使问题化繁为简，化难为易，复杂问题也能迎刃而解．

例：当代数式 $x^{2} + 3 x + 5$ 的值为7时，求代数式 $3 x^{2} + 9 x － 2$ 的值．

解：因为 $x^{2} + 3 x + 5 = 7$ ，所以 $x^{2} + 3 x = 2$ ．

所以． $3 x^{2} + 9 x － 2 = 3 （ x^{2} + 3 x ）－ 2 = 3 \times 2 － 2 = 4$

以上方法是典型的整体代入法．

请根据阅读材料，解决下列问题：

(1)、已知 $a^{2} + 3 a － 2 = 0$ ，求 $5 a^{3} + 15 a^{2} － 10 a + 2020$ 的值．

(2)、我们知道方程 $x^{2} + 2 x － 3 = 0$ 的解是 $x_{1} = 1 ， x_{2} = － 3$ ，现给出另一个方程 $（ 2 x + 3 ）^{2} + 2 （ 2 x + 3 ）－ 3 = 0$ ，则它的解是．

查看试题解析
23. 两个边长分别为a和b的正方形如图放置（图1），其未叠合部分（阴影）面积为S₁；若再在图1中大正方形的右下角摆放一个边长为b的小正方形（如图2），两个小正方形叠合部分（阴影）面积为S₂

(1)、用含a ， b的代数式分别表示S₁ ， S₂；

(2)、若a+b＝10，ab＝23，求S₁+S₂的值；

(3)、当S₁+S₂＝28时，求出图3中的阴影部分的面积S₃.

查看试题解析
24. 阅读下面材料，然后解答问题：
解方程：(x²-6)³-(x²-6)-2=0.
分析：本题实际上为一元四次方程，若展开按常规方法解答，对同学们来说具有一定的挑战性.解高次方程的基本方法是“降次”，我们发现本方程是以 $x^{2} - 6$ 为基本结构搭建的，所以我们可以把 $x^{2} - 6$ 视为一个整体，设为另外一个未知数，就可以把原方程降次为一元二改方程来继续解答.我们把这种换元解方程的方法叫做换元法.
解：设 $x^{2} - 6 = m$ ，则原方程换元为 $m^{2} - m - 2 = 0$ .
$∴ (m - 2) (m + 1) = 0 ，$ $∴ m - 2 = 0$ 或 $m + 1 = 0 .$
解得 $m_{1} = 2 ， m_{2} = - 1 ，$
$∴ x^{2} - 6 = 2$ 或 $x^{2} - 6 = - 1$
解得： $x_{1} = 2 \sqrt{2} ， x_{2} = - 2 \sqrt{2} ， x_{3} = \sqrt{5} ， x_{4} = - \sqrt{5} .$
请参考例题解法，解下列方程：

(1)、 $x^{4} - 5 x^{2} + 6 = 0$ ；

(2)、 $x^{2} + 3 x - \sqrt{x^{2} + 3 x} - 2 = 0$ .

查看试题解析

2024年中考数学热点探究二 整体思想在求值中的运用

一、选择题（每题3分，共30分）

二、填空题（每题3分，共15分）

三、解答题（共9题，共75分）

2024年中考数学热点探究二整体思想在求值中的运用