2024年中考数学热点探究一实数与数轴的关系

试卷更新日期：2024-04-27 类型：二轮复习

进入出卷网下载

一、选择题（每题3分，共30分）

1. 如图所示，点 $C$ 的表示的数为 $2$ ， $B C ＝ 1$ ，以 $O$ 为圆心， $O B$ 为半径画弧，交数轴于点 $A$ ，则点 $A$ 表示的数是（）

A、 $\sqrt{3}$ B、 $\sqrt{5}$ C、 $- \sqrt{3}$ D、 $- \sqrt{5}$

查看试题解析
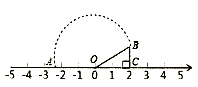2. 实数x、y在数轴上的位置如图所示，化简 $\sqrt{(x - y)^{2}}$ 的结果是（）

A、 $x - y$ B、 $x + y$ C、 $- x - y$ D、 $y - x$

查看试题解析
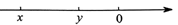3. 在数轴上表示实数 $a$ 和 $b$ 的点的位置如图所示，那么下列各式成立的是（）

A、 $a < b$ B、 $a > b$ C、 $a b > 0$ D、 $| a | > | b |$

查看试题解析
4. 一个正数x的两个不同的平方根分别是 $2 a + 3$ 和 $a - 9$ ．如图，在数轴上表示实数 $\sqrt[3]{x + 3 a}$ 的点是（）

A、点N B、点M C、点Q D、点P

查看试题解析
5. 如图，面积为2的正方形 $A B C D$ 的顶点C在数轴上，且表示的数为 $- 1$ .若将正方形 $A B C D$ 绕点C逆时针旋转，使点D落到数轴上的点P处，则点P在数轴上所对应的数为（）

A、 $\sqrt{2} - 1$ B、 $\sqrt{2} + 1$ C、 $- \sqrt{2} + 1$ D、 $- \sqrt{2} - 1$

查看试题解析
6. 实数 $a$ 在数轴上对应的点的位置如图所示，则 $\sqrt{{(a - 4)}^{2}} - \sqrt{{(a - 11)}^{2}}$ 化简后为（）

A、 $7$ B、 $- 7$ C、 $15 - 2 a$ D、 $2 a - 15$

查看试题解析
7. 已知实数a在数轴上的对应点的位置如图所示，则化简 $| a - 1 | - \sqrt{{(a - 2)}^{2}}$ 的结果是（）

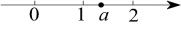A、3-2a B、-1 C、1 D、2a-3

查看试题解析
8. 数轴上A、B、C三点所代表的数分别是m、2、n且 $| m - n | - | m - 2 | = | n - 2 |$ ．则下列选项中，表示A、B、C三点在数轴上的位置关系正确的是（）

A、 B、 C、 D、

查看试题解析
9. 若实数a ， b在数轴上的位置如图所示，则化简 $\sqrt{4 a^{2}} + 2 | a + b |$ 的结果为（）

A、－4a－2b B、－2a＋b C、－2b D、4a－2b

查看试题解析
10. 有理数a，b，c在数轴上的位置如图所示：则代数式 $| a + c | - 2 | a - b | + | b - c |$ 化简后的结果为（）

A、b B、 $a - 3 b$ C、 $b + 2 c$ D、 $b - 2 c$

查看试题解析

二、填空题（每题4分，共20分）

11. 已知A ， B ， C三点在数轴上对应的数为a ， b ， c ，它们在数轴上的位置如图所示，化简： $| a + b + c | - | c - b - a | =$ ．

查看试题解析
12. 实数a ， b在数轴上的位置如图所示，化简： $\sqrt{(a + 1)^{2}} + | b - 1 | - \sqrt{(a + b)^{2}} =$ ．

查看试题解析
13. 已知有理数a、b、c在数轴上的位置如图所示，化简： $| a - b | - | b - c | + | c - a | =$ ．

查看试题解析
14. 如图，在数轴上点 $A$ ，点 $B$ 表示的数分别是 $- 5$ ， $3$ ，点 $P$ 在数轴上，若 $P A = 3 P B$ ，则点 $P$ 表示的数是．

查看试题解析
15. 如图，面积为 $a (a > 1)$ 的正方形 $A B C D$ 的边 $A B$ 在数轴上，点 $B$ 表示的数为1．将正方形 $A B C D$ 沿着数轴水平移动，移动后的正方形记为 $A^{'} B^{'} C D^{'}$ ，点 $A 、 B 、 C 、 D$ 的对应点分别为 $A^{'} 、 B^{'} 、 C 、 D^{'}$ ，移动后的正方形 $A^{'} B^{'} C D^{'}$ 与原正方形 $A B C D$ 重叠部分图形的面积记为 $S$ ．当 $S = \frac{1}{2} \sqrt{a}$ 时，数轴上点 $A^{'}$ 表示的数是（可用含 $a$ 的代数式表示）．

查看试题解析

三、解答题（共5题，共54分）

16. 实数a、b在数轴上的位置如图所示．化简 $\sqrt{a^{2}} - \sqrt{b^{2}} + \sqrt{{(a - b)}^{2}}$ ．

查看试题解析
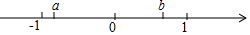17.

(1)、已知实数a，b，c在数轴上的对应点的位置如图所示，化简： $\sqrt{(- a + b)^{2}} + \sqrt{(c - b)^{2}} - \sqrt{(b - c - a)^{2}}$ .

(2)、若 $\sqrt{5}$ 的整数部分为a，小数部分为b，写出a，b的值，并计算 $\frac{a - 1}{b} - a b$ 的值.

查看试题解析
18. 已知 $A$ 、 $B$ 在数轴上对应的数分别用 $a$ 、 $b$ 表示，且 ${(\frac{1}{2} a b + 10)}^{2} + | a - 2 | = 0$ ，点 $P$ 是数轴上的一个动点．

(1)、求出 $A$ 、 $B$ 之间的距离；

(2)、若 $P$ 到点 $A$ 和点 $B$ 的距离相等，求出此时点 $P$ 所对应的数；

(3)、数轴上一点 $C$ 距 $A$ 点 $3 \sqrt{6}$ 个单位长度，其对应的数 $c$ 满足 $| a c | = - a c$ ．当 $P$ 点满足 $P B = 2 P C$ 时，求 $P$ 点对应的数．

查看试题解析
19. 如图①是由8个同样大小的立方体组成的魔方，体积为8．

(1)、求出这个魔方的棱长；

(2)、图①中阴影部分是一个正方形 $A B C D$ ，求出阴影部分的面积及其边长．

(3)、把正方形 $A B C D$ 放到数轴上，如图②，使得点 $A$ 与-1重合，那么点 $D$ 在数轴上表示的数为．

查看试题解析
20. 如图，数轴上，点 $A$ ， $B$ 表示的数分别为 $a$ ， $b$ ，点 $P$ 为负半轴上任意一点，它表示的数为 $x$ ．

(1)、计算 $\frac{| a - b | + a + b}{2}$ 的值；

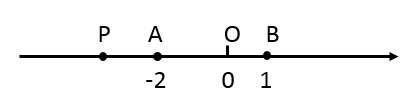(2)、在 $a ， b ， x$ 中，其中一个数是另两个数的平均数，求 $x$ 的值；

(3)、嘉琪认为：当 $- 2 \leq x < 0$ 时， $P O + P A < A B$ ，则以 $P O ， P A ， A B$ 的长为边长不能构成三角形．若以 $P O ， P A ， A B$ 的长为边长能构成三角形，请直接写出 $x$ 的取值范围．

查看试题解析

四、实践探究题（共16分）

21.

(1)、【算一算】

如图①，点A、B、C在数轴上，B为AC的中点，点A表示-3，点B表示1，则点C表示的数为， AC长等于；

(2)、【找一找】
如图②，点M、N、P、Q中的一点是数轴的原点，点A、B分别表示实数 $\frac{\sqrt{2}}{2}$ -1、 $\frac{\sqrt{2}}{2}$ +1，Q是AB的中点，则点是这个数轴的原点；

(3)、【画一画】
如图③，点A、B分别表示实数c-n、c+n，在这个数轴上作出表示实数n的点E（要求：尺规作图，不写作法，保留作图痕迹）；

(4)、【用一用】
学校设置了若干个测温通道，学生进校都应测量体温，已知每个测温通道每分钟可检测a个学生.凌老师提出了这样的问题：假设现在校门口有m个学生，每分钟又有b个学生到达校门口.如果开放3个通道，那么用4分钟可使校门口的学生全部进校；如果开放4个通道，那么用2分钟可使校门口的学生全部进校.在这些条件下，a、m、b会有怎样的数量关系呢？
爱思考的小华想到了数轴，如图④，他将4分钟内需要进校的人数m+4b记作+(m+4b)，用点A表示；将2分钟内由4个开放通道检测后进校的人数，即校门口减少的人数8a记作-8a，用点B表示.
①用圆规在小华画的数轴上分别画出表示+（m+2b）、-12a的点F、G，并写出+(m+2b)的实际意义；
②写出a、m的数量关系：　　.

查看试题解析

2024年中考数学热点探究一 实数与数轴的关系

一、选择题（每题3分，共30分）

二、填空题（每题4分，共20分）

三、解答题（共5题，共54分）

四、实践探究题（共16分）

2024年中考数学热点探究一实数与数轴的关系