【北师大版·数学】2024年中考二轮复习之勾股定理
试卷更新日期：2024-04-27 类型：二轮复习
一、选择题
-
1. 勾股定理是人类早期发现并证明的重要数学定理之一，是用代数思想解决几何问题的最重要的工具之一，也是数形结合的纽带之一．它不但因证明方法层出不穷吸引着人们，更因为应用广泛而使人入迷．如图，秋千静止时，踏板离地的垂直高度 ， 将它往前推至处时（即水平距离），踏板离地的垂直高度 ， 它的绳索始终拉直，则绳索的长是（ ）
A、 B、 C、6 D、2. 下列四组数据中，不能作为直角三角形的三边长的是（ ）A、7，24，25 B、8，15，17 C、5，11，12 D、3，4，53. 直角三角形的两条直角边的长分别为6和8，则斜边长为（ ）A、10 B、5 C、4 D、34. 如图，AB，BC，CD，DE是四根长度均为5cm的火柴棒，点A，C，E共线，若AC=6cm，CD⊥BC，则线段CE的长度是（ ）
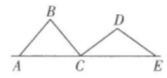A、6cm B、7cm C、6cm D、8cm5. 如图，AD是等腰三角形ABC的顶角平分线，AB=5，BC=6，则AD等于 （ ）
A、10 B、5 C、4 D、36. 如图，四边形 是边长为9的正方形纸片，将其沿 折叠，使点 落在 边上的点 处，点 的对应点为点 ， ，则 的长为（ ）
A、1.8 B、2 C、2.3 D、7. 若直角三角形的一条直角边长为9，斜边长为10，则另一条直角边长为（ ）．A、1 B、 C、19 D、38. 如图，分别以 的三边为斜边向外作等腰直角三角形，若斜边 ，则图中阴影部分的面积为（ ）．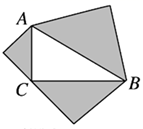
A、6 B、12 C、16 D、189. 如图，梯子AB靠在墙上，梯子的底端A到墙根O的距离为5m，梯子的顶端B到地面的距离为12m，现将梯子的底端A向外移动到A'，使梯子的底端A'到墙根O的距离等于6m，同时梯子的顶端B下降至B'，那么BB'（ ）
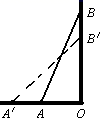A、小于1m B、大于1m C、等于1m D、小于或等于1m10. 勾股定理是几何中的一个重要定理，在我国古算书《周髀算经》中就有“若勾三，股四，则弦五”的记载.如图1是由边长相等的小正方形和直角三角形构成的，可用其面积关系验证勾股定理.图2是由图1放入矩形内得到的， ， ， .点D，E，F，G，H，I都在矩形 的边上，则矩形 的面积为（ ）．
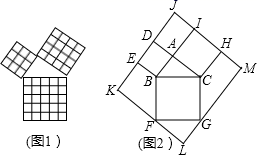A、288 B、400 C、432 D、440二、填空题
-
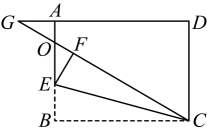
11. 如图，在长方形中， ， ， 点E为上一点，将沿翻折至 ， 延长交于点O ， 交的延长线于点G ， 且 ， 则的长为 ．
12. 如图，已知△ABC与△A'B'C'是以坐标原点O为位似中心的位似图形，且=.若点A的坐标为（-1，0），点C的坐标为（ ， 1），则A'C'=.
13. 如图，A，B两地之间有一座山，汽车原来从A地到B地需途经C地沿折线ACB行驶，开通隧道后，汽车可直接沿线段AB行驶。已知BC=80km，∠A=45°，∠B=30°，则开通隧道后，汽车从A地到B地的路程大约有km.（结果精确到0.1km，参考数据：1.41，1.73）
14. 动手操作：在长方形纸片ABCD中，AB＝6，AD＝10．如图所示，折叠纸片，使点A落在BC边上的A′处，折痕为PQ ， 当点A′在BC边上移动时，折痕的端点P、Q也随之移动．若限定点P、Q分别在AB、AD边上移动，则点A′在BC边上可移动的最大距离为 ．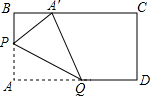
15. 有一架竖直靠在直角墙面的梯子正在下滑，一只猫紧紧盯住位于梯子正中间的老鼠，等待与老鼠距离最小时扑捉．把墙面、梯子、猫和老鼠都理想化为同一平面内的线或点，模型如图， ，点 ， 分别在射线 ， 上， 长度始终保持不变， ， 为 的中点，点 到 ， 的距离分别为4和2．在此滑动过程中，猫与老鼠的距离 的最小值为 ．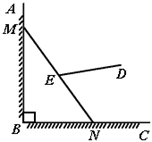
三、解答题
-
16. 如图，小刚想知道学校旗杆的高度，他发现旗杆顶端A处的绳子垂到地面B处后还多2米当他把绳子拉直并使下端刚好接触到地面C处，发现绳子下端到旗杆下端的距离为6米，请你帮小刚求出旗杆的高度AB长．
17. 学校运动场上垂直竖立的旗杆的顶端A系有一根升旗用的绳子，绳子垂直到地面时还剩1米长在地面（如图①），小芳为了测量旗杆AB的高度，将绳子拉直，使绳子的另一端C刚好着地（如图②）．量得BC＝5米，求旗杆AB的高度．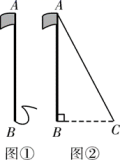
18. 已知△ABC中，AB＝AC，CD⊥AB于D，若AB＝5，CD＝3，求BC的长．
19. 如图，在△ABC中，∠ADC＝∠BDC＝90°，AC＝20，BC＝15，BD＝9，求AD的长．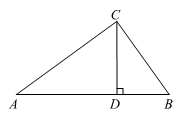
四、综合题
-
20. 如图，在△ABC和△DCE中，AC=DE，∠B=∠DCE=90°，点A，C，D在同一直线上，且AB∥DE，连接AE.
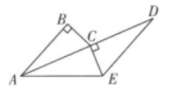(1)、求证：△ABC≌△DCE.(2)、当BC=5，AC=12时，求AE的长.21. 如图，长方形纸片ABCD中，AB＝8，BC＝10，折叠纸片的一边AD，使点D落在BC边上的点F处，AE为折痕．请回答下列问题：
(1)、AF＝；(2)、试求线段DE的长度．22. 如图，等边△ABC中，A ， B关于y轴对称，AD⊥AC交y轴负半轴于点D ， C（0，6）．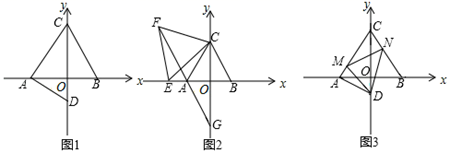
(1)、如图1，求D点坐标；(2)、如图2，E为x轴负半轴上任一点，以CE为边作等边△CEF ， FA的延长线交y轴于点G ， 求OG的长；(3)、如图3，在（1）的条件下，以D为顶点作60°的角，它的两边分别与CA、BC交于点MN ， 连接MN ． 探究线段AM、MN、NB之间的关系，并予以证明．23. 如图，在△ABC中，AB=15，BC=14，AC=13，求△ABC的面积． 某学习小组经过合作交流，给出了下面的解题思路，请你按照他们的解题思路，完成解答过程．
(1)、作AD⊥BC于D，设BD=x，用含x的代数式表示CD，则CD=(2)、请根据勾股定理，利用AD作为“桥梁”建立方程，并求出x的值；(3)、利用勾股定理求出AD的长，再计算三角形的面积．