【北师大版·数学】2024年中考二轮复习之平行四边形
试卷更新日期:2024-04-27 类型:二轮复习
一、选择题
-
1. 如果一个正多边形的内角和是900°,则这个正多边形是( )A、正七边形 B、正九边形 C、正五边形 D、正十边形2. 如图,在平行四边形ABCD中,E,F分别在边BC,AD上,添加选项中的条件后不能判定四边形AECF是平行四边形的是( ).
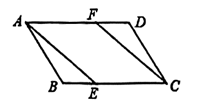 A、BE = DF B、AECF C、AF = EC D、AE = EC3. 如图,在▱ABCD中AB为⊙O的直径,⊙O与DC相切于点E,与AD相交于点F,已知AB=12,∠C=60°,则 的长为( )
A、BE = DF B、AECF C、AF = EC D、AE = EC3. 如图,在▱ABCD中AB为⊙O的直径,⊙O与DC相切于点E,与AD相交于点F,已知AB=12,∠C=60°,则 的长为( ) A、 B、 C、 D、24. 如图,在▱ABCD中,AE平分∠BAD且交BC于点E,∠D=58°,则∠AEC的大小是 ( )
A、 B、 C、 D、24. 如图,在▱ABCD中,AE平分∠BAD且交BC于点E,∠D=58°,则∠AEC的大小是 ( )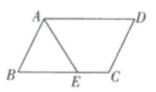 A、61° B、109° C、119° D、122°5. 如图,在Rt△ABC中,∠ACB=90°,CD为中线,延长CB至点E,使BE=BC,连接DE,F为DE中点,连接BF,若AC=8,BC=6,则BF的长为( )
A、61° B、109° C、119° D、122°5. 如图,在Rt△ABC中,∠ACB=90°,CD为中线,延长CB至点E,使BE=BC,连接DE,F为DE中点,连接BF,若AC=8,BC=6,则BF的长为( ) A、2 B、2.5 C、3 D、46. 如图,在四边形ABCD中,对角线AC和BD相交于点O,下列条件不能判定四边形ABCD是平行四边形的是( )
A、2 B、2.5 C、3 D、46. 如图,在四边形ABCD中,对角线AC和BD相交于点O,下列条件不能判定四边形ABCD是平行四边形的是( ) A、AB∥DC,AD∥BC B、AB= DC,AD=BC C、AB∥DC,AD=BC D、OA=OC,OB=OD7. 如图,E是▱ABCD的边AD上的点,且= , 连接BE并延长,交CD的延长线于点F,若DE=DF=3,则▱ABCD的周长为( )
A、AB∥DC,AD∥BC B、AB= DC,AD=BC C、AB∥DC,AD=BC D、OA=OC,OB=OD7. 如图,E是▱ABCD的边AD上的点,且= , 连接BE并延长,交CD的延长线于点F,若DE=DF=3,则▱ABCD的周长为( ) A、15 B、24 C、30 D、368. 一个多边形的内角和是1080°,则这个多边形的边数是 ( )A、9 B、8 C、7 D、69. 中,点 分别是 的边 , 的中点,连接 ,若 ,则 ( )A、 B、 C、 D、10. 如图,E,F分别是▱ABCD的边AD、BC上的点,EF=6,∠DEF=60°,将四边形EFCD沿EF翻折,得到EFC′D′,ED′交BC于点G,则△GEF的周长为( )
A、15 B、24 C、30 D、368. 一个多边形的内角和是1080°,则这个多边形的边数是 ( )A、9 B、8 C、7 D、69. 中,点 分别是 的边 , 的中点,连接 ,若 ,则 ( )A、 B、 C、 D、10. 如图,E,F分别是▱ABCD的边AD、BC上的点,EF=6,∠DEF=60°,将四边形EFCD沿EF翻折,得到EFC′D′,ED′交BC于点G,则△GEF的周长为( ) A、6 B、12 C、18 D、24
A、6 B、12 C、18 D、24二、填空题
-
11. 如图,在▱ABCD中,AD=10,对角线AC 与BD相交于点O,AC+BD=22,则△BOC的周长为
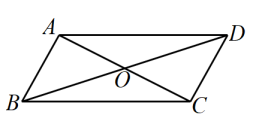 12. 如图,以平行四边形ABCO的顶点O为原点,边OC所在直线为x轴,建立平面直角坐标系,顶点C的坐标是(2,0),tan∠AOC=2,过点A的反比例函数的图象过BC边的中点D,则k的值是 .
12. 如图,以平行四边形ABCO的顶点O为原点,边OC所在直线为x轴,建立平面直角坐标系,顶点C的坐标是(2,0),tan∠AOC=2,过点A的反比例函数的图象过BC边的中点D,则k的值是 . 13. 如图,在Rt△ABC中,∠ACB=90°,D,E,F分别是AB,AC,AD的中点,若EF=3,则AB的长为.
13. 如图,在Rt△ABC中,∠ACB=90°,D,E,F分别是AB,AC,AD的中点,若EF=3,则AB的长为. 14. 如图,已知▱ABCD,AD⊥BD,AC=10,AD=4,则BD的长是.
14. 如图,已知▱ABCD,AD⊥BD,AC=10,AD=4,则BD的长是. 15. 正十边形每个内角的度数为.
15. 正十边形每个内角的度数为.三、解答题
-
16. 如图,在线段AD上有两点E,F,且AE=DF,过点E,F分别作AD的垂线BE和CF,连接AB,CD,BF,CE,且AB∥CD.求证:四边形BECF是平行四边形。
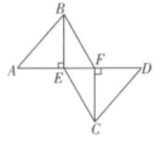 17. 如图,在平行四边形ABCD中,BE=DF . 求证:CE=AF .
17. 如图,在平行四边形ABCD中,BE=DF . 求证:CE=AF .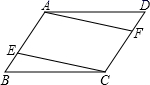 18. 已知:如图,在平行四边形ABCD中,AE⊥BD,CF⊥BD,垂足分别为E,F.求证:△ADE≌△CBF.
18. 已知:如图,在平行四边形ABCD中,AE⊥BD,CF⊥BD,垂足分别为E,F.求证:△ADE≌△CBF.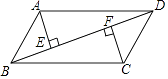 19. 如图,在▱ABCD中,E、F为对角线BD上的两点,且∠BAE=∠DCF.求证:BE=DF.
19. 如图,在▱ABCD中,E、F为对角线BD上的两点,且∠BAE=∠DCF.求证:BE=DF.
四、综合题
-
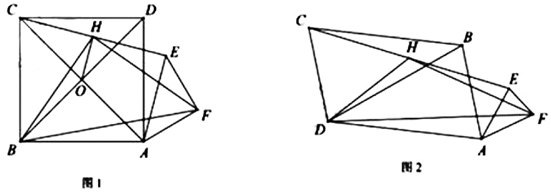
20. 在正方形 中,等腰直角 , ,连接 ,H为 中点,连接 、 、 ,发现 和 为定值.
 (1)、① ▲ ;
(1)、① ▲ ;② ▲ .
③小明为了证明①②,连接 交 于O , 连接 ,证明了 和 的关系,请你按他的思路证明①②.
(2)、小明又用三个相似三角形(两个大三角形全等)摆出如图2, , ( )求① (用k的代数式表示)
② (用k、 的代数式表示)
21. 平行四边形中,点E在边上,连 , 点F在线段上,连 , 连 . (1)、如图1,已知 , 点E为中点, . 若 , 求的长度;(2)、如图2,已知 , 将射线沿翻折交于H,过点C作交于点G.若 , 求证:;(3)、如图3,已知 , 若 , 直接写出的最小值.22. 如图,在ABC中,BC=2AB,AD是BC边上的中线,O是AD的中点,过点A作AEBC,交BO的延长线于点E,BE交AC于点F,连接DE交AC于点G.
(1)、如图1,已知 , 点E为中点, . 若 , 求的长度;(2)、如图2,已知 , 将射线沿翻折交于H,过点C作交于点G.若 , 求证:;(3)、如图3,已知 , 若 , 直接写出的最小值.22. 如图,在ABC中,BC=2AB,AD是BC边上的中线,O是AD的中点,过点A作AEBC,交BO的延长线于点E,BE交AC于点F,连接DE交AC于点G. (1)、判断四边形ABDE的形状,并说明理由;(2)、若 , 且OA:OB=3:5,求四边形ABDE的面积;(3)、连接DF,求证:DF2=FG•FC.
(1)、判断四边形ABDE的形状,并说明理由;(2)、若 , 且OA:OB=3:5,求四边形ABDE的面积;(3)、连接DF,求证:DF2=FG•FC.