【北师大版·数学】2024年中考二轮复习之图形的平移与旋转
试卷更新日期:2024-04-27 类型:二轮复习
一、选择题
-
1. 下列标志中,既是中心对称图形,也是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 在平面直角坐标系中,将点向左平移2个单位长度,再向上平移2个单位长度所得到的点坐标为( )A、 B、 C、 D、3. 在平面直角坐标系中,将点A(5,7)向右平移5个单位长度得到点B,则点B关于y轴的对称点B’的坐标为( )A、(5,-12) B、(-10,7) C、(10,-7) D、(5,-7)4. 如图,将△AOB绕着点O顺时针旋转,得到△COD,若∠AOB=40°,∠BOC=30°,则旋转角度是( )
2. 在平面直角坐标系中,将点向左平移2个单位长度,再向上平移2个单位长度所得到的点坐标为( )A、 B、 C、 D、3. 在平面直角坐标系中,将点A(5,7)向右平移5个单位长度得到点B,则点B关于y轴的对称点B’的坐标为( )A、(5,-12) B、(-10,7) C、(10,-7) D、(5,-7)4. 如图,将△AOB绕着点O顺时针旋转,得到△COD,若∠AOB=40°,∠BOC=30°,则旋转角度是( ) A、10° B、30° C、40° D、70°5. 如图所示的圆锥,下列说法正确的是( )
A、10° B、30° C、40° D、70°5. 如图所示的圆锥,下列说法正确的是( )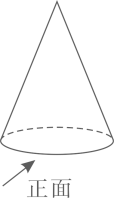 A、该圆锥的主视图是轴对称图形 B、该圆锥的主视图是中心对称图形 C、该圆锥的主视图既是轴对称图形,又是中心对称图形 D、该圆锥的主视图既不是轴对称图形,又不是中心对称图形6. 如图,已知A(3,1)与B(1,0),PQ是直线 上的一条动线段且 (Q在P的下方),当AP+PQ+QB最小时,Q点坐标为( )
A、该圆锥的主视图是轴对称图形 B、该圆锥的主视图是中心对称图形 C、该圆锥的主视图既是轴对称图形,又是中心对称图形 D、该圆锥的主视图既不是轴对称图形,又不是中心对称图形6. 如图,已知A(3,1)与B(1,0),PQ是直线 上的一条动线段且 (Q在P的下方),当AP+PQ+QB最小时,Q点坐标为( )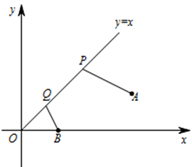 A、( , ) B、( , ) C、(0,0) D、(1,1)7. 如图,△ABC中,BC=8,AD是中线,将△ADC沿AD折叠至△ADC′,发现CD与折痕的夹角是60°,则点B到C′的距离是( )
A、( , ) B、( , ) C、(0,0) D、(1,1)7. 如图,△ABC中,BC=8,AD是中线,将△ADC沿AD折叠至△ADC′,发现CD与折痕的夹角是60°,则点B到C′的距离是( ) A、4 B、 C、 D、38.
A、4 B、 C、 D、38.正方形ABCD在坐标系中的位置如图所示,将正方形ABCD绕D点顺时针旋转90°后,B点的坐标为( )
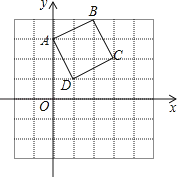 A、(﹣2,2) B、(4,1) C、(3,1) D、(4,0)9.
A、(﹣2,2) B、(4,1) C、(3,1) D、(4,0)9.如图,ABCD是一块长方形纸板.试画一条直线,将它的面积分成相等的两部分,那么这种直线能画( )
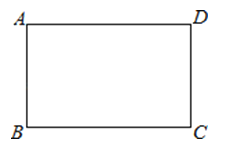 A、2条 B、4条 C、8条 D、无数条10.
A、2条 B、4条 C、8条 D、无数条10.在如图所示的平面直角坐标系中,△OA1B1是边长为2的等边三角形,作△B2A2B1与△OA1B1关于点B1成中心对称,再作△B2A3B3与△B2A2B1关于点B2成中心对称,如此作下去,则△B2nA2n+1B2n+1(n是正整数)的顶点A2n+1的坐标是( )
 A、(4n﹣1,) B、(2n﹣1,) C、(4n+1,) D、(2n+1,)
A、(4n﹣1,) B、(2n﹣1,) C、(4n+1,) D、(2n+1,)二、填空题
-
11. 已知点与点关于原点对称,则 .12. 在平面直角坐标系中,将点A(1,-2)向上平移3个单位长度,再向左平移2个单位长度,得到点A’,则点A'的坐标是.13. 如图,在平面直角坐标系中,△A'B'O与△ABO关于坐标原点O中心对称,若点A(2,1)向上平移三个单位可以得到点B,则点B的对应点B′的坐标为.
 14. 如图,已知△ABC三个顶点的坐标分别为A(0,4),B(-1,1),C(-2,2).将△ABC向右平移4个单位,得到△A'B'C',点A,B,C的对应点分别为A',B,C',再将△A'B'C'绕点B'顺时针旋转90°,得到△A"B"C",点A', B',C'的对应点分别为A",B",C",则点A"的坐标为.
14. 如图,已知△ABC三个顶点的坐标分别为A(0,4),B(-1,1),C(-2,2).将△ABC向右平移4个单位,得到△A'B'C',点A,B,C的对应点分别为A',B,C',再将△A'B'C'绕点B'顺时针旋转90°,得到△A"B"C",点A', B',C'的对应点分别为A",B",C",则点A"的坐标为. 15. 如图,平面直角坐标系xOy中,将四边形ABCD先向下平移,再向右平移得到四边形A1B1C1D1已知A(-3,5),B(-4,3),A1(3,3),则点B1标为.
15. 如图,平面直角坐标系xOy中,将四边形ABCD先向下平移,再向右平移得到四边形A1B1C1D1已知A(-3,5),B(-4,3),A1(3,3),则点B1标为.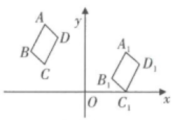
三、作图题
-
16. 线段在平面直角坐标系中的位置如图7所示,其中每个小正方形的边长为1个单位长度.

⑴将线段向左平移6个单位长度,作出平移后的线段;
⑵再将线段绕点顺时针旋转180°后得到线段;
⑶观察线段和线段 , 它们是否关于某点成中心对称?若是,请写出对称中心的坐标.
四、解答题
-
17. 如图 , 点为平面直角坐标系的原点,点在轴上,是边长为的等边三角形.
 (1)、求点的坐标;(2)、若将绕点顺时针旋转 , 则点的对应点的坐标是;(3)、将沿着轴向右平移到处,如图 , 连接 , 交于点判断的形状,并说明理由.18. 如图,将平行四边形ABCD向左平移2个单位长度,得到平行四边形A'B'C'D',画出平移后的图形,并指出其各个顶点的坐标.
(1)、求点的坐标;(2)、若将绕点顺时针旋转 , 则点的对应点的坐标是;(3)、将沿着轴向右平移到处,如图 , 连接 , 交于点判断的形状,并说明理由.18. 如图,将平行四边形ABCD向左平移2个单位长度,得到平行四边形A'B'C'D',画出平移后的图形,并指出其各个顶点的坐标. 19.
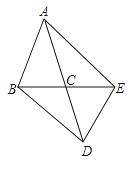
19.如图,在△ABC中,AB=AC,△ABC与△DEC关于点C成中心对称,连接AE、BD.
(1)线段AE、BD具有怎样的位置关系和大小关系?说明你的理由.
(2)如果△ABC的面积为5cm2 , 求四边形ABDE的面积.
(3)当∠ACB为多少度时,四边形ABDE为矩形?说明你的理由.
五、实践探究题
-
20. 问题情境:在学习图形的平移和旋转时,数学兴趣小组遇到这样一个问题:如图 , 点为等边的边上一点,将线段绕点逆时针旋转得到线段 , 连接 .
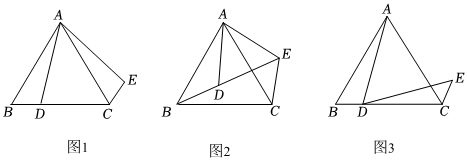 (1)、【猜想证明】试猜想与的数量关系,并加以证明;(2)、【探究应用】如图 , 点为等边内一点,将线段绕点逆时针旋转得到线段 , 连接 , 若、、三点共线,求证:平分;(3)、【拓展提升】如图 , 若是边长为的等边三角形,点是线段上的动点,将线段绕点顺时针旋转得到线段 , 连接点在运动过程中,的周长最小值直接写答案 .
(1)、【猜想证明】试猜想与的数量关系,并加以证明;(2)、【探究应用】如图 , 点为等边内一点,将线段绕点逆时针旋转得到线段 , 连接 , 若、、三点共线,求证:平分;(3)、【拓展提升】如图 , 若是边长为的等边三角形,点是线段上的动点,将线段绕点顺时针旋转得到线段 , 连接点在运动过程中,的周长最小值直接写答案 .六、综合题
-
21. 如图所示的正方形网格中,△ABC的顶点均在格点上,请在所给直角坐标系中按要求画图:
 (1)、作出△ABC关于坐标原点O成中心对称的△A1B1C1;(2)、作出以点A旋转中心,将△ABC绕点A顺时针旋转90°得到的△A2B2C2;(3)、点C2的坐标为.
(1)、作出△ABC关于坐标原点O成中心对称的△A1B1C1;(2)、作出以点A旋转中心,将△ABC绕点A顺时针旋转90°得到的△A2B2C2;(3)、点C2的坐标为.
-
-