【北师大版·数学】2024年中考二轮复习之一元一次不等式(组)
试卷更新日期:2024-04-27 类型:二轮复习
一、选择题
-
1. 不等式组 的解集是( ).A、 B、 C、 D、2. 不等式 的解集在数轴上表示为( )A、
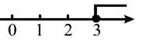 B、
B、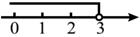 C、
C、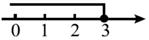 D、
D、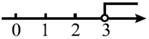 3. 不等式组的解集在数轴上表示为( )A、
3. 不等式组的解集在数轴上表示为( )A、 B、
B、 C、
C、 D、
D、 4. 某校拟用不超过2600元的资金在新华书店购买党史和改革开放史书籍共40套来供学生借阅,其中党史每套72元,改革开放史每套60元,那么学校最多可以购买党史书籍多少套?设学校可以购买党史书籍x套,根据题意得( )A、72x+60(40﹣x)≤2600 B、72x+60(40﹣x)<2600 C、72x+60(40﹣x)≥2600 D、72x+60(40﹣x)=26005. 定义:不大于实数x的最大整数称为x的整数部分,记作 , 例如 , 按此规定,若 , 则x的取值范围为( )A、 B、 C、 D、6. 已知 , 下列选项正确的是( )A、 B、 C、 D、7. 对于实数 , 定义符号其意义为:当时,;当时, . 例如: , 若关于的函数 , 则该函数的最大值是( )A、1 B、 C、 D、28. 某班数学兴趣小组对不等式组 , 讨论得到以下结论:
4. 某校拟用不超过2600元的资金在新华书店购买党史和改革开放史书籍共40套来供学生借阅,其中党史每套72元,改革开放史每套60元,那么学校最多可以购买党史书籍多少套?设学校可以购买党史书籍x套,根据题意得( )A、72x+60(40﹣x)≤2600 B、72x+60(40﹣x)<2600 C、72x+60(40﹣x)≥2600 D、72x+60(40﹣x)=26005. 定义:不大于实数x的最大整数称为x的整数部分,记作 , 例如 , 按此规定,若 , 则x的取值范围为( )A、 B、 C、 D、6. 已知 , 下列选项正确的是( )A、 B、 C、 D、7. 对于实数 , 定义符号其意义为:当时,;当时, . 例如: , 若关于的函数 , 则该函数的最大值是( )A、1 B、 C、 D、28. 某班数学兴趣小组对不等式组 , 讨论得到以下结论:①若 , 则不等式组的解集为;
②若 , 则不等式组无解;
③若不等式组有解,则a的取值范围;
④若不等式组只有四个整数解,则a的值只可以为7;
其中,正确结论的个数是( )
A、1个 B、2个 C、3个 D、4个9. 如果不等式组的解集是x<3,那么m的取值范围是( )A、m< B、m≥ C、m<3 D、m≥310. 关于x的方程3﹣2x=3(k﹣2)的解为非负整数,且关于x的不等式组有解,则符合条件的整数k的值之和为( )A、5 B、4 C、3 D、2二、填空题
-
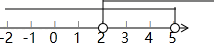
11. 某商品进价4元,标价5元出售,商家准备打折销售,但其利润率不能少于10%,则最多可打折.12. 不等式组的解集是.13. 不等式(x-2)<3的解集是.14. 不等式组的所有整数解的和是 .15. 一个关于x的不等式组的解集在数轴上表示为,则这个不等式组的解集是 .
三、计算题
-
16. 解不等式组: .17. 解不等式:2(x﹣1)<4﹣x .
四、解答题
-
18. 当自变量x满足什么条件时,的函数值不小于的函数值?19. 解不等式组 ,并写出不等式组的非负整数解.20. 某历史文化街区需要加装一批垃圾分类提示牌和垃圾箱.根据需求,提示牌比垃圾箱多5个,且提示牌和垃圾箱的个数之和不少于100个,则至少购买垃圾箱多少个?21. 甲、乙两个仓库向A、B两地运送水泥,已知甲库可调出100吨水泥,乙库可调出80吨水泥,A地需70吨,B地需110吨水泥,两库到A,B两地的路程和费用如下表:(表中运费“元/吨·千米”表示每吨水泥运送1千米所需要人民币).
路程(千米)
运费(元/吨·千米)
甲库
乙库
甲库
乙库
A地
20
15
12
12
B地
25
20
10
8
设甲库运往A地水泥x吨,总运费W元.
(1)、写出w关于x的函数关系式,并求x为何值时总运费最小?(2)、如果要求运送的水泥数是10吨的整数倍,且运费不能超过38000元,则总共有几种运送方案?五、综合题
-
22. 定义运算 min{a,b}:当 a≥b 时,min{a,b}=b;当 a<b 时,min{a,b}=a;如:min{4,0}=0;min{2,2}=2;min{﹣3,﹣1}=﹣3.根据该定义运算完成下列问题:
 (1)、min{﹣3,2}= , 当 x≤3 时,min{x,3}=;(2)、如图,已知直线 y1=x+m 与 y2=kx﹣2 相交于点 P(﹣2,1),若 min{x+m,kx﹣2}=kx﹣2,结合图象,直接写出 x 的取值范围是;(3)、若 min{3x﹣1,﹣x+3}=3﹣x,求 x 的取值范围.
(1)、min{﹣3,2}= , 当 x≤3 时,min{x,3}=;(2)、如图,已知直线 y1=x+m 与 y2=kx﹣2 相交于点 P(﹣2,1),若 min{x+m,kx﹣2}=kx﹣2,结合图象,直接写出 x 的取值范围是;(3)、若 min{3x﹣1,﹣x+3}=3﹣x,求 x 的取值范围.