【北师大版·数学】2024年中考二轮复习之三角形的证明
试卷更新日期:2024-04-27 类型:二轮复习
一、选择题
-
1. 如图,四边形 内有一点 , , ,若 ,则 的大小是( )
 A、 B、 C、 D、2. 如果将长为6cm,宽为5cm的长方形纸片折叠一次,那么这条折痕的长不可能是( )
A、 B、 C、 D、2. 如果将长为6cm,宽为5cm的长方形纸片折叠一次,那么这条折痕的长不可能是( )
A、8cm B、5cm C、5.5cm D、1cm3. 如图,直线l:分别与x轴、y轴交于点A、B . 点P为直线l在第一象限的点.作△POB的外接圆 , 延长OC交于点D , 当△POD的面积最小时,则的半径长为( )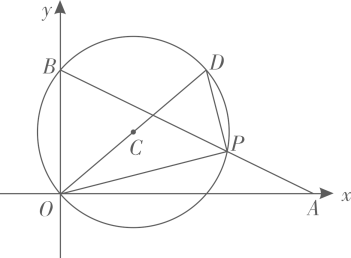 A、 B、2 C、 D、34. 下列命题中,是真命题的有( ).
A、 B、2 C、 D、34. 下列命题中,是真命题的有( ).①全等三角形的对应边相等;②有两个角为的三角形一定是等边三角形;③两条直线被第三条直线所截,内错角相等;④等腰三角形的角平分线和中线相互重合.
A、1个 B、2个 C、3个 D、4个5. 命题:已知 , . 求证: . 运用反证法证明这个命题时,第一步应假设( )成立A、 B、 C、 D、且6. 如图,AC=BC=BE=DE=10cm,点A、B、D在同一条直线上,AB=12cm,BD=16cm,则点C和点E之间的距离是( ) A、6cm B、7cm C、8cm D、7. 如图,在中,分别以点A和点B为圆心,大于的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD.若的周长为17, , 则的周长为( )
A、6cm B、7cm C、8cm D、7. 如图,在中,分别以点A和点B为圆心,大于的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD.若的周长为17, , 则的周长为( ) A、8 B、9 C、10 D、118. 如图,在Rt△ABC中,∠ACB=90°,∠A=30°,CD是斜边AB上的高,BD=2,那么AD的长为( )
A、8 B、9 C、10 D、118. 如图,在Rt△ABC中,∠ACB=90°,∠A=30°,CD是斜边AB上的高,BD=2,那么AD的长为( )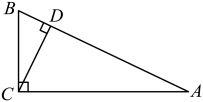 A、2 B、4 C、6 D、89. 如图, , , 平分 , 则的度数为( )
A、2 B、4 C、6 D、89. 如图, , , 平分 , 则的度数为( )
 A、 B、 C、 D、10. 如图,每个小正方形的边长为1,在△ABC中,点D为AB的中点,则线段CD的长为( )
A、 B、 C、 D、10. 如图,每个小正方形的边长为1,在△ABC中,点D为AB的中点,则线段CD的长为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
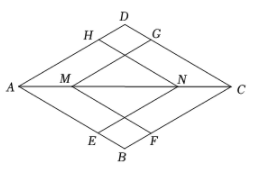
11. 如图,在菱形ABCD中, AB=1,∠BAD=60°.在其内部作形状、大小都相同的菱形 AENH 和菱形 CGMF ,使点E,F,G,H分别在边 AB、BC、CD、DA 上,点M,N在对角线 AC 上.若 AE=3BE,则 MN 的长为 .
 12. 如图,在中, , , 点D为上一动点,连接 , 将沿翻折得到 , 交于点G, , 且 , 则 .
12. 如图,在中, , , 点D为上一动点,连接 , 将沿翻折得到 , 交于点G, , 且 , 则 .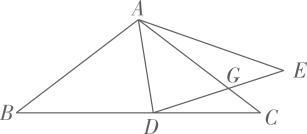 13. 某城市几条道路的位置关系如图所示,道路 , 道路与的夹角 . 城市规划部门想新修一条道路BF,要求 , 则的度数为 .
13. 某城市几条道路的位置关系如图所示,道路 , 道路与的夹角 . 城市规划部门想新修一条道路BF,要求 , 则的度数为 . 14. 如图,OC是∠AOB的平分线,点P是OC上一点,PM⊥OB于点M,点N是射线OA上一动点,若PM=7,则PN的最小值为。
14. 如图,OC是∠AOB的平分线,点P是OC上一点,PM⊥OB于点M,点N是射线OA上一动点,若PM=7,则PN的最小值为。 15. 如图,在△ABC中,AB=5,AC=7,直线DE垂直平分BC,垂足为E,交AC于点D,则△ABD的周长是.
15. 如图,在△ABC中,AB=5,AC=7,直线DE垂直平分BC,垂足为E,交AC于点D,则△ABD的周长是.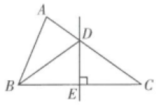
三、作图题
-
16. 如图,正方形网格中的两个小正方形的边长都是 ,每个小正方形的顶点叫格点,一个顶点为格点的三角形称为格点三角形:
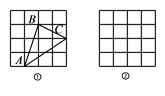 (1)、如图①,已知格点 ,则 (是或不是)直角三角形:(2)、画一个格点 ,使其为钝角三角形,且面积为17. 如图,已知△ABC,用尺规作出△ABC外心.(保留作图痕迹,不写作法)
(1)、如图①,已知格点 ,则 (是或不是)直角三角形:(2)、画一个格点 ,使其为钝角三角形,且面积为17. 如图,已知△ABC,用尺规作出△ABC外心.(保留作图痕迹,不写作法)
四、解答题
-
18. 2023年5月30日,神舟十六号载人飞船发射取得圆满成功,3名航天员顺利进驻中国空间站,如图中的照片展示了中国空间站上机械臂的一种工作状态,当两臂 , 两臂夹角时,求A,B两点间的距离.(结果精确到 , 参考数据 , , )
 19. 如图,已知 ,点P在 上, , ,垂足分别为D,E.求证: .
19. 如图,已知 ,点P在 上, , ,垂足分别为D,E.求证: . 20. 如图,AD是Rt△ABC斜边上的高。若AB=4,BC=10,求BD的长.
20. 如图,AD是Rt△ABC斜边上的高。若AB=4,BC=10,求BD的长. 21. 如图,已知 平分 , .求证: .
21. 如图,已知 平分 , .求证: .
五、实践探究题
-
22. 已知四边形ABCD中,E , F分别是AB , AD边上的点,DE与CF交于点G , 令=k .
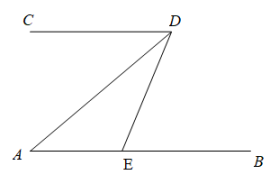
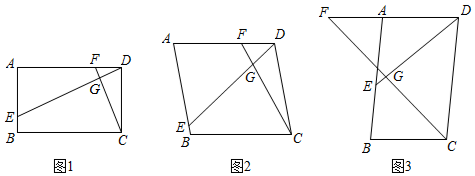 (1)、特例解析:如图1,若四边形ABCD是矩形,且DE⊥CF , 求证:=k;(2)、类比探究:如图2,若四边形ABCD是平行四边形,当∠B与∠EGC满足什么关系时,=k仍然成立?并证明你的结论;(3)、拓展延伸:如图3,在(2)的条件下, , ∠AED=45°,求DE的长.
(1)、特例解析:如图1,若四边形ABCD是矩形,且DE⊥CF , 求证:=k;(2)、类比探究:如图2,若四边形ABCD是平行四边形,当∠B与∠EGC满足什么关系时,=k仍然成立?并证明你的结论;(3)、拓展延伸:如图3,在(2)的条件下, , ∠AED=45°,求DE的长.六、综合题
-
23. 如图,在四边形ABCD中, ,点E是AC的中点,且
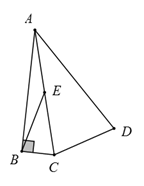 (1)、尺规作图:作 的平分线AF , 交CD于点F , 连结EF、BF(保留作图痕迹,不写作法);(2)、在(1)所作的图中,若 ,且 ,证明: 为等边三角形.
(1)、尺规作图:作 的平分线AF , 交CD于点F , 连结EF、BF(保留作图痕迹,不写作法);(2)、在(1)所作的图中,若 ,且 ,证明: 为等边三角形.
-