云南省昆明市二中2023-2024学年九年级下学期开学数学试卷

试卷更新日期：2024-04-26 类型：开学考试

进入出卷网下载

一、选择题：本题共15小题，每小题2分，共30分．在每小题给出的选项中，只有一项是符合题目要求的．

1. 滇池亦称昆明湖、昆明池、滇南泽、滇海，位于昆明市西山区，是云南省面积最大的高原湖泊，也是全国第六大淡水湖，有着“高原明珠”之称滇池的蓄水量大约为 $1290000000$ 立方米．数字 $1290000000$ 用科学记数法可以表示为（）

A、 $1.29 \times 1 0^{9}$ B、 $12.9 \times 1 0^{8}$ C、 $0.129 \times 1 0^{10}$ D、 $1.29 \times 1 0^{10}$

查看试题解析
2. 剪纸艺术是最古老的中国民间艺术之一，先后入选中国国家级非物质文化遗产名录和人类非物质文化遗产代表作名录.鱼与“余”同音，寓意生活富裕、年年有余，是剪纸艺术中很受喜爱的主题.以下关于鱼的剪纸中，是轴对称图形但不是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 下列由4个大小相同的正方体搭成的几何体，从左面看得到的图形与其它几何体从左面看得到的图形不同的是（）

A、 B、 C、 D、

查看试题解析
4. 将一把直尺和一块含有 $30 °$ 的直角三角板按如图所示的位置摆放，若 $∠ 1 = 33 °$ ，则 $∠ 2$ 为（　　）

A、 $63 °$ B、 $107 °$ C、 $117 °$ D、 $120 °$

查看试题解析
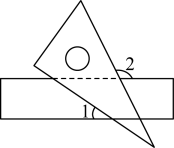5. 下列运算正确的是（）

A、a⁶÷a²＝a³ B、 $\frac{a + 1}{a} - \frac{1}{a} = a (a \neq 0)$ C、（﹣2a）³＝﹣6a³ D、a³•a²＝a⁵

查看试题解析
6. 不等式组 $\{\begin{matrix} 3 - x \geq 0 \\ - 2 x - 4 > 0 \end{matrix}$ 的解集在数轴上表示正确的是（）

A、 B、 C、 D、

查看试题解析
7. 一个凸多边形的内角和比它的外角和的 3 倍还多 180°，则这个多边形是（）

A、九边形 B、八边形 C、七边形 D、六边形

查看试题解析
8. 已知点A（1，﹣3）关于y轴的对称点A^'在反比例函数y＝ $\frac{k}{x}$ 的图象上，则实数k的值为（）

A、3 B、 $\frac{1}{3}$ C、﹣3 D、﹣ $\frac{1}{3}$

查看试题解析
9. 下列说法错误的是（）

A、为了解全省九年级学生每天完成作业的时间的情况，采用抽样调查 B、两条直线相交所形成的对顶角相等是必然事件 C、甲、乙两人各自测试坐位体前屈10次，若他们成绩的平均数相同，甲的成绩的方差为0.36，乙的成绩的方差为0.6，则乙的表现较甲更稳定 D、某种彩票的中奖率是0.0001%，表示该种彩票中奖的可能性非常小

查看试题解析
10. 如图，⊙O是△ABC的外接圆，若∠BAC＝45°，⊙O半径为2，则劣弧 $\hat{B C}$ 的长为（）

A、2 $\sqrt{2}$ B、4 C、 $\frac{π}{2}$ D、π

查看试题解析
11. 如图，在△ABC中，AD平分∠BAC ，按如下步骤作图：
第一步，分别以点A、D为圆心，以大于 $\frac{1}{2}$ AD的长为半径在AD两侧作弧，交于两点M、N；
第二步，连接MN分别交AB、AC于点E、F；
第三步，连接DE、DF ．
若BD＝6，CD＝3，CF＝2，则AE的长是（）

A、3 B、4 C、5 D、6

查看试题解析
12. 按一定顺序排列的单项式：﹣2x ， 4x³ ， ﹣8x⁵ ， 16x⁷ ， ﹣32x⁹ ， 64x¹¹ ， …，第n个单项式是（）

A、2ⁿxⁿ⁺¹ B、2ⁿxⁿ^﹣1 C、（﹣2）ⁿx²ⁿ^﹣1 D、（﹣2）ⁿx²ⁿ⁺¹

查看试题解析
13. 关于x的一元二次方程kx²﹣4x+2＝0有实数根，则k的取值范围是（）

A、k＝2 B、k≥2且k≠0 C、k≤2 D、k≤2且k≠0

查看试题解析
14. 新能源汽车环保节能，越来越受到消费者的喜爱．各种品牌相继投放市场．一汽贸公司经销某品牌新能源汽车．去年销售总额为5000万元，今年1～5月份，每辆车的销售价格比去年降低1万元．销售数量与去年一整年的相同．销售总额比去年一整年的少20%，今年1﹣5月份每辆车的销售价格是多少万元？设今年1﹣5月份每辆车的销售价格为x万元．根据题意，列方程正确的是（）

A、 $\frac{5000}{x + 1}$ = $\frac{5000 (1 - 20 %)}{x}$ B、 $\frac{5000}{x + 1}$ = $\frac{5000 (1 + 20 %)}{x}$ C、 $\frac{5000}{x - 1}$ = $\frac{5000 (1 - 20 %)}{x}$ D、 $\frac{5000}{x - 1}$ = $\frac{5000 (1 + 20 %)}{x}$

查看试题解析
15. 如图，在△ABC中，AB＝AC，MN是边BC上一条运动的线段（点M不与点B重合，点N不与点C重合），且MN＝ $\frac{1}{2}$ BC，MD⊥BC交AB于点D，NE⊥BC交AC于点E，在MN从左至右的运动过程中，设BM＝x，△BMD的面积减去△CNE的面积为y，则下列图象中，能表示y与x的函数关系的图象大致是（）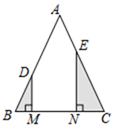

A、 B、 C、 D、

查看试题解析

二、填空题：本题共4小题，每小题2分，共8分.

16. 要使式子 $\frac{\sqrt{x - 5}}{3}$ 有意义，x的取值范围是．

查看试题解析
17. 分解因式： $3 x^{3} + 6 x^{2} + 3 x =$ ．

查看试题解析
18. 如果两个相似三角形的面积比为3：4，那么它们对应高之比为．

查看试题解析
19. 如图，在等腰△ABC中，AB＝AC＝10cm ， BC＝16cm ，点D由点A出发沿AB方向向点B匀速运动，同时点E由点B出发沿BC方向向点C匀速运动，它们的速度均为1cm/s ，连接DE ，设运动时间为ts（0＜t＜10），当△BDE与△ABC相似时，t的值为 s ．

查看试题解析

三、解答题：本题共8小题，共62分.解答应写出文字说明，证明过程或演算步骤

20. 计算： ${(\frac{1}{2})}^{- 1} - \sqrt{9} + 2 s i n 60 ° + {(π - \sqrt{10})}^{0} + | \sqrt{3} - 2 |$ ．

查看试题解析
21. 已知：如图，点A、B、C、D在一条直线上，EA∥FB ， EA＝FB ， AB＝CD ．

(1)、求证：EC＝FD；

(2)、若∠A＝40°，∠D＝80°，求∠E的度数．

查看试题解析
22. 2022年3月25日，教育部印发《义务教育课程方案和课程标准（2022年版）》，优化了课程设置，将劳动从综合实践活动课程中独立出来.某校为了解该校学生一周的课外劳动情况，随机抽取部分学生调查了他们一周的课外劳动时间，将数据进行整理并制成如下统计图.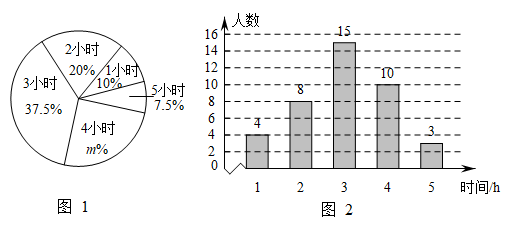
请根据图中提供的信息，解答下面的问题：

(1)、求图1中的m= ，本次调查数据的中位数是h，本次调查数据的众数是h；

(2)、该校此次抽查的这些学生一周平均的课外劳动时间是多少？

(3)、若该校共有2000名学生，请根据统计数据，估计该校学生一周的课外劳动时间不小于 $3 h$ 的人数.

查看试题解析
23. 中国共产党第二十次全国代表大会于2022年10月16日至2022年10月22日在北京胜利召开．为了增进全校学生对二十大有关知识的了解．某校团委举行了关于二十大知识的竞赛活动，最终A ， B ， C ， D这四名同学在本次活动中获得了一等奖，其中A ， B ， C是女生，D是男生．

(1)、若校团委决定从获得一等奖的这四名同学中随机选取一名同学在总结大会上发言，则选取的这名同学是女生的概率为；

(2)、若校团委决定从获得一等奖的这四名同学中随机选取两名同学在总结大会上发言，请用列表或画树状图的方法求选取的两名同学是一名女生和一名男生的概率．

查看试题解析
24. 如图，在 $▱ A B C D$ 中， $C D = B D$ ， DE平分∠BDC交BC于点O，交AB的延长线于点E，连接CE．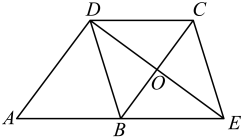

(1)、求证：四边形BECD是菱形；

(2)、如果 $A B = 5$ ， $A D = 6$ ，求四边形BECD的面积．

查看试题解析
25. 某市准备在一个广场上种植甲、乙两种花卉．经市场调查，甲种花卉的种植费用y（元）与种植面积x（m²）的函数关系如图所示，乙种花卉的种植费用为每平方米100元．

(1)、求y与x的函数关系式；

(2)、甲、乙两种花卉种植面积共1200m² ，其中，甲种花卉的种植面积x满足300＜x≤800，怎样分配甲、乙两种花卉种植面积才能使种植费用最少？最少种植费用是多少？

查看试题解析
26. 如图，AB是⊙O的直径，C为⊙O上一点，连接AC ， BC ，延长AB至点D ，使得∠DCB＝∠CAB ，点E为 $\hat{A B}$ 的中点，连接CE交AB于点F ，连接BE ．

(1)、求证：DC为⊙O的切线；

(2)、若CD＝4，tan∠CEB＝ $\frac{1}{2}$ ，求CF•CE ．

查看试题解析
27. 在平面直角坐标系中，O为坐标原点，直线y＝﹣x+3与x轴交于点B ，与y轴交于点C ．二次函数y＝ax²+2x+c的图象过B ， C两点，且与x轴交于另一点A ，点M为线段OB上的一个动点（不与端点O ， B重合）．

(1)、求二次函数的表达式；

(2)、如图①，过点M作y轴的平行线l交BC于点F ，交二次函数y＝ax²+2x+c的图象于点E ，记△CEF的面积为 $S_{1}$ ， △BMF的面积为 $S_{2}$ ，当 $\frac{S_{1}}{S_{2}} = \frac{1}{2}$ 时，求点E的坐标；

(3)、如图②，连接CM ，过点M作CM的垂线l₁ ，过点B作BC的垂线l₂ ， l₁与l₂交于点G ，试探究 $\frac{C G}{C M}$ 的值是否为定值？若是，请求出 $\frac{C G}{C M}$ 的值；若不是，请说明理由．

查看试题解析