河北省石家庄市赵县2023-2024学年七年级下学期月考数学试题

试卷更新日期：2024-04-26 类型：月考试卷

进入出卷网下载

一、选择题（本大题共16个小题，共38分，1~6小题，每小题3分；7~16小题，每小题2分，在每小题给出的四个选项中，只有一项是符合题目要求的）

1. 数学源于生活，用于生活，我们要会用数学的眼光观察现实世界，会用数学的思维思考现实世界，会用数学的语言表达现实世界，如图所示，生活中木匠弹墨线、打靶瞄准、拉绳插秧等场景，就反映了直线的一个基本事实是（）

A、经过两点，有且仅有一条直线 B、经过一点，有无数条直线 C、垂线段最短 D、两点之间，线段最短

查看试题解析
2. 如图， $△ A B C$ 是等腰直角三角形， $a ∥ b$ .若 $∠ 1 = 125 °$ ，则 $∠ 2$ 的度数是（）

A、30° B、35° C、40° D、45°

查看试题解析
3. 9的平方根是（）

A、3 B、 $- 3$ C、 $\pm 3$ D、没有平方根

查看试题解析
4. 直线 $A B, B C, C A$ 的位置关系如图所示，则下列语句不正确的是（）

A、点 $A$ 在直线 $A C$ 上 B、直线 $A B, B C, C A$ 两两相交 C、点 $A$ 是直线 $A B, A C$ 的交点 D、直线 $B C$ 经过点 $A$

查看试题解析
5. 下列说法中正确的个数是（）
① ${(- 3)}^{2}$ 的平方根是 $+ 3$ ；② $- m^{2}$ 没有平方根；③非负数a的平方根是非负数；④负数没有平方根；⑤0和1的平方根等于本身

A、1个 B、2个 C、3个 D、4个

查看试题解析
6. 如图所示，下列推理正确的个数是（）
①若 $∠ 1 = ∠ 2$ ，则 $A B ∥ C D$ ②若 $A D ∥ B C$ ，则 $∠ 3 + ∠ A = 180 °$
③若 $∠ C + ∠ C D A = 180 °$ ，则 $A D ∥ B C$ ④若 $A B ∥ C D$ ，则 $∠ 3 = ∠ 4$

A、0个 B、1个 C、2个 D、3个

查看试题解析
7. 下列说法中，正确的是（）

A、两点之间直线最短 B、如果∠α＝53°38'，那么∠α余角的度数为36.22° C、如果一个角的余角和补角都存在，那么这个角的余角比这个角的补角小 D、相等的角是对顶角

查看试题解析
8. 如图为商场某品牌椅子的侧面图， $∠ D E F = 121 °$ ， $D E$ 与地面平行， $∠ A B D = 48 °$ ，则 $∠ D C E =$ （）

A、78° B、73° C、69° D、61°

查看试题解析
9. 如图， $A B = 6$ ，点A到直线 $B C$ 的距离为3，若在射线 $B C$ 上只存在一个点 $P$ ，记 $A P$ 的长度为 $d$ ，则 $d$ 的值可以是（）

A、7 B、2 C、5 D、6

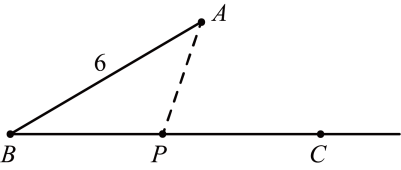查看试题解析
10. 如图， $A B ∥ E F$ ，设 $∠ C = 90 °$ ，那么x、y和z的关系是（）

A、 $y = x + z$ B、 $x + y - z = 90 °$ C、 $x + y + z = 180 °$ D、 $y + z - x = 90 °$

查看试题解析
11. 已知 $2 m - 4$ 与 $m - 5$ 是同一个数的平方根，则m的值是（）

A、 $- 3$ B、1 C、 $- 1$ 或3 D、 $- 3$ 或1

查看试题解析
12. 若 $a$ ， $b$ 为实数，且 $| a + 2 | + \sqrt{b - \frac{1}{2}} = 0$ ，则 ${(a b)}^{2024}$ 的值为（）

A、0 B、1 C、 $- 1$ D、 $\pm 1$

查看试题解析
13. 如图， $△ A B C$ 平移到 $△ D E F$ 的位置，则下列说法：① $A B ∥ D E$ ， $A D = C F = B E$ ；② $∠ A C B = ∠ D E F$ ；③平移的方向是点C到点F的方向；④平移距离为线段BD的长其中说法正确的有（）

A、①② B、①③ C、①④ D、②④

查看试题解析
14. 若 $\sqrt{{(x - 3.5)}^{2}} = 3.5 - x$ ，则x的值不能是（）

A、4 B、3 C、2 D、1

查看试题解析
15. 如图，△ABC中，∠ACB＝90°，AC＝3，BC＝4，AB＝5，P为直线AB上一动点，连接PC，则线段PC的最小值是（）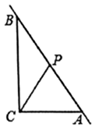

A、3 B、2.5 C、2.4 D、2

查看试题解析
16. 大、中、小三个正方形摆放如图所示，若大正方形的面积为5，小正方形的面积为1，则正方形 $A B C D$ 的边长可能是（）

A、1 B、 $\sqrt{3}$ C、 $\sqrt{5}$ D、3

查看试题解析

二、填空题（本大题共3个小题，共10分.17题2分，其中18~19小题各4分，每空2分）

17. $\sqrt{81}$ 的算术平方根是

查看试题解析
18. 如图是一种对顶角量角器，它所测量的角的度数是，用它测量角的原理是.

查看试题解析
19. 如图，直线 $A B$ 、 $C D$ 相交于点O ， $O E$ 平分 $∠ B O C$ .
⑴若 $∠ A O D = α$ ，则 $∠ A O E =$ .（用含 $α$ 的式子表示）
⑵若 $∠ A O D = 68 °$ ， $O F ⊥ C D$ ，则 $∠ E O F =$ .

查看试题解析

三、解答题（本大题共7个小题，共72分.解答应写出文字说明、证明过程或演算步骤）

20. 求下列各数的算术平方根：

(1)、64

(2)、0.25

(3)、 $\frac{49}{81}$

(4)、 $1 0^{- 2}$

查看试题解析
21. 如图，点O是直线AB上一点，∠AOC=40°，OD平分∠AOC，∠COE=70°.

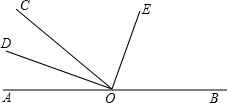(1)、请你说明DO⊥OE；

(2)、OE平分∠BOC吗？为什么？

查看试题解析
22. 实数a ， b在数轴上的位置如图所示.

(1)、化简： $\sqrt{a^{2}} =$ ， $| a + b | =$ ；

(2)、先化简，再求值： $\sqrt{{(a + 1)}^{2}} + \sqrt{{(b - 2)}^{2}}$ ，其中a是 $\frac{1}{4}$ 的一个平方根，b是3的算术平方根.

查看试题解析
23. 完成下面的证明：
如图，已知： $A D ⊥ B C$ ， $F G ⊥ B C$ ，垂足分别为D、G ，且 $∠ 1 = ∠ 2$ ，求证： $∠ B D E = ∠ C$ .
证明：∵ $A D ⊥ B C$ ， $F G ⊥ B C$ （已知），
$∴$ $∠ A D C = 90 °$ ， $∠ F G C = 90 °$ （①    ▲    ），
$∴$ $∠ A D C = ∠ F G C$ （②     ▲     ），
$∴$ $A D ∥ F G$ （③    ▲    ），
$∴$ $∠ 1 =$ ④     ▲    （⑤     ▲    ）.
又∵ $∠ 1 = ∠ 2$ （已知），
$∴$ $∠ 3 =$ ⑥   ▲   （⑦     ▲     ），
$∴$ $D E ∥ A C$ （⑧     ▲    ），
$∴$ $∠ B D E = ∠ C$ （⑨   ▲    ）.

查看试题解析
24. 如图，直线 $A B$ 、 $C D$ 相交于点O ， $O F ⊥ C D$ ， $O E$ 平分 $∠ B O D$ .

(1)、若 $∠ A O C = 68 °$ ，求 $∠ E O F$ 的度数；

(2)、若 $∠ B O E$ 比 $∠ B O F$ 大24°，求 $∠ C O E$ 的度数.

查看试题解析
25. 喜欢探索数学知识的小明遇到一个新的定义：对于三个正整数，若其中任意两个数乘积的算术平方根都是整数，则称这三个数为“和谐组合”，其结果中最小的整数称为“最小算术平方根”，最大的整数称为“最大算术平方根”，例：1，4，9这三个数， $\sqrt{1 \times 4} = 2$ ， $\sqrt{1 \times 9} = 3$ ， $\sqrt{4 \times 9} = 6$ ，其结果分别为2，3，6，都是整数，所以1，4，9三个数称为“和谐组合”，其中最小算术平方根是2，最大算术平方根是6.

(1)、请直接判断3，12，32是不是“和谐组合”，.

(2)、请证明2，18，8这三个数是“和谐组合”，并求出最小算术平方根和最大算术平方根.

(3)、已知9，a ， 25三个数是“和谐组合”，且最大算术平方根是最小算术平方根的3倍，求a的值.

查看试题解析
26. 如图1，直线 $A B$ 与直线 $l_{1}$ 、 $l_{2}$ 分别交于C ， D两点，点M在直线 $l_{2}$ 上，射线 $D E$ 平分 $∠ A D M$ 交直线 $l_{1}$ 于点Q ， $∠ A C Q = 2 ∠ C D Q$ .

(1)、证明： $l_{1} ∥ l_{2}$ ；

(2)、如图2，点P是 $C D$ 上一点，射线 $Q P$ 交直线 $l_{2}$ 于点F ， $∠ A C Q = 70 °$ .
①若 $∠ Q F D = 20 °$ ，直接写出 $∠ F Q D$ 的度数是 ▲ ；
②点N在射线 $D E$ 上，满足 $∠ Q C N = ∠ Q F D$ ，连接 $C N$ ，请补全图形，探究 $∠ C N D$ 与 $∠ F Q D$ 满足的等量关系，并证明.

查看试题解析