河北省石家庄长安区2024年中考一模数学试题

试卷更新日期：2024-04-26 类型：中考模拟

进入出卷网下载

一、选择题（本大题共16个小题．1-6小题每小题3分，7-16小题每小题2分，共38分．在每小题给出的四个选项中，只有一项是符合题目要求的）

1. $- 2$ 比2（）

A、小2 B、大2 C、小4 D、大4

查看试题解析
2. 一艘轮船在P处向M处的海上巡逻艇呼叫救援，根据图所示，巡逻艇从M处去P处实施救援，若要航线最短，其航行的路线为（）

A、沿北偏东 $40 °$ 方向航行 B、沿南偏西 $50 °$ 方向航行 C、沿北偏东 $40 °$ 方向，航行30海里 D、沿南偏西 $40 °$ 方向，航行30海里

查看试题解析
3. 为纪念我国著名数学家苏步青所做的卓越贡献，国际上将一颗距地球2.18亿千米的行星命名为“苏步青星”，将2.18亿用科学记数法表示为 $2.18 \times 1 0^{n}$ ，则 $n =$ （）

A、8 B、6 C、4 D、2

查看试题解析
4. 若使用如图所示的a ， b两根直铁丝做成一个三角形框架，需要将其中一根铁丝折成两段，则可以分为两段的铁丝是（）

A、a ， b都可以 B、a ， b都不可以 C、只有a可以 D、只有b可以

查看试题解析
5. 整式 $A = x - 1$ ， $B = x^{2} - x$ ，下列结论：
结论一： $A \cdot x = B$ ．
结论二：A ， B的公因式为x ．
下列判断正确的是（）

A、结论一正确，结论二不正确 B、结论一不正确，结论二正确 C、结论一、结论二都正确 D、结论一、结论二都不正确

查看试题解析
6. 如图，将由6个棱长为1的小正方体组成的几何体在桌面上逆时针旋转 $90 °$ 后，主视图的面积为（）

A、3 B、4 C、5 D、6

查看试题解析
7. 在课堂上老师给出了一道分式化简题：化简 $(\frac{a}{a - b} - 1) \div \frac{b}{a^{2} - b^{2}}$ ，以下变形过程正确的是（）

A、原式 $= \frac{a}{a - b} - 1 \cdot \frac{a^{2} - b^{2}}{b}$ B、原式 $= \frac{a - a - b}{a - b} \div \frac{b}{a^{2} - b^{2}}$ C、原式 $= \frac{a - a + b}{a - b} \cdot \frac{b}{a^{2} - b^{2}}$ D、原式 $= \frac{a - a + b}{a - b} \cdot \frac{a^{2} - b^{2}}{b}$

查看试题解析
8. 如图 $∠ 1 = 70 °$ ， $∠ 2 = 150 °$ ，则直线 $A B$ 与 $C D$ 所成的锐角的度数是（）

A、 $20 °$ B、 $30 °$ C、 $40 °$ D、 $50 °$

查看试题解析
9. 如图，数轴上有①，②，③，④四部分，数轴上的三个点分别表示数a ， b ， c且 $a < 0$ ， $a b c > 0$ ，则原点落在（）

A、段① B、段② C、段③ D、段④

查看试题解析
10. 如图，四边形 $A B C D$ 中，点E ， F ， G ， H分别是线段 $A B$ ， $C D$ ， $A C$ ， $B D$ 的中点，对于四边形 $E G F H$ 的周长，下列说法正确的是（）

A、只与线段 $A B$ ， $C D$ 的长有关 B、只与线段 $A D$ ， $B C$ 的长有关 C、只与线段 $A C$ ， $B D$ 的长有关 D、与四边形 $A B C D$ 各边的长都有关

查看试题解析
11. 班主任和甲、乙、丙三位同学围坐在圆桌前．如图，班主任坐在了D座位，三位同学随机坐在A ， B ， C三个座位，则甲、乙两位同学座位相邻的概率是（）

A、 $\frac{1}{2}$ B、 $\frac{1}{3}$ C、 $\frac{1}{4}$ D、 $\frac{2}{3}$

查看试题解析
12. 如图，在正方形纸片 $A B C D$ 上进行如下操作：
第一步：剪去长方形纸条 $A E F D$ ；
第二步：从长方形纸片 $B C F E$ 上剪去长方形纸条 $C F G H$ ．
若长方形纸条 $A E F D$ 和 $C F G H$ 的面积相等，则 $A B$ 的长度为（）

A、 $30 c m$ B、 $15 c m$ C、 $16 c m$ D、 $90 c m$

查看试题解析
13. 刘阿姨早晨从家里出发去公园锻炼，匀速走了 $60 m i n$ 后回到家（中间不休息）．下图表示她出发后离家的距离 $s (k m)$ 与行走时间 $t (m i n)$ 之间的函数关系图象．则下列图形中可以大致描述刘阿姨行走路线的是（）

A、 B、 C、 D、

查看试题解析
14. 对于题目“已知 $⊙ O$ 及圆外一点P ，如何过点P作出 $⊙ O$ 的切线？”甲、乙的作法如图：
甲的作法
连接 $O P$ ，作 $O P$ 的垂直平分线交 $O P$ 于点G ，以点G为圆心， $O G$ 长为半径画弧交 $⊙ O$ 于M ，作直线 $P M$ ．直线．即为所求．
乙的作法
连接 $P O$ 并延长，交 $⊙ O$ 于B ， C两点，分别，以P ， O为圆心， $P O$ ， $B C$ 长为半径作弧，两弧交于点D ，连接 $O D$ ，交 $⊙ O$ 于点M ，作直线 $P M$ ．直线 $P M$ 即为所求．
下列说法正确的是（）

A、甲和乙的作法都正确 B、甲和乙的作法都错误 C、甲的作法正确，乙的作法错误 D、乙的作法正确，甲的作法错误

查看试题解析
15. 如图，直线 $y = 2 x + 2$ 及反比例函数 $y = \frac{k}{x} (x > 0)$ 的图象与两坐标轴之间的阴影部分（不包括边界）有5个整点（横、纵坐标都为整数），则k的取值可能是（）

A、2 B、3 C、4 D、5

查看试题解析
16. 如图，矩形 $A B C D$ 中，点E ， F ， G分别在边 $A B$ ， $C D$ ， $A D$ 上，将矩形分别沿 $G E$ ， $G F$ ， $E C$ 折叠，使点A ， D恰好都落在点O处，点B落在点 $B^{'}$ 处．以下结论：
Ⅰ：若点 $B^{'}$ 落在 $E F$ 上，则 $G F / / E C$ ．
Ⅱ：若点 $B^{'}$ 与点O重合，则 $A B = A D$ ．
下列判断正确的是（）

A、Ⅰ、Ⅱ都正确 B、Ⅰ、Ⅱ都不正确 C、只有Ⅰ正确 D、只有Ⅱ正确

查看试题解析

二、填空题（本大题有3个小题，共10分．17小题2分，18~19小题各4分，每空2分）

17. 计算： $\sqrt{4} - \sqrt{9}$ = ．

查看试题解析
18. 规定一种新运算： $a ☆ b = a b + a - b$ ，如 $2 ☆ 3 = 2 \times 3 + 2 - 3 = 5$ ．
⑴计算： $(3 a) ☆ 5 =$ ；
⑵如果 $2 ☆ (2 x - 3) = 3 x^{2} - 2$ ，则x的值为．

查看试题解析
19. 图1是一种拼装玩具的零件，它可以看作是底面为正六边形的六棱柱，其内部挖去一个底面为正方形的长方体后得到的几何体，图2是该零件的俯视图，正方形 $A B C D$ 的两个相对的顶点A ， C分别在正六边形一组平行的对边上，另外两个顶点B ， D在正六边形内部（包括边界），点E ， F分别是正六边形的顶点．已知正六边形的边长为2，正方形边长为a ．
⑴连接 $E F$ ， $E F$ 的长为；
⑵a的取值范围是．

查看试题解析

三、解答题（本大题有7个小题，共72分．解答应写出文字说明、证明过程或演算步骤）

20. 琪琪准备完成题目：计算： $(- 9) \times (\frac{1}{2} - ■) - 3^{3}$ ．发现题中有一个数字“■”被墨水污染了．

(1)、琪琪猜测被污染的数字“■” $\frac{2}{3}$ ，请计算 $(- 9) \times (\frac{1}{2} - \frac{2}{3}) - 3^{3}$ ；

(2)、琪琪的妈妈看到该题标准答案的结果等于 $- 9$ ，请通过计算求出被污染的数字“■”．

查看试题解析
21. 某班数学小组在研究个位数字为5的两位数的平方的规律时，得到了下列等式：
第1个等式： $1 5^{2} = 15 \times 15 = 225 = (1 \times 2) \times 100 + 25$ ；
第2个等式： $2 5^{2} = 25 \times 25 = 625 = (2 \times 3) \times 100 + 25$ ；
第3个等式： $3 5^{2} = 35 \times 35 = 1225 = (3 \times 4) \times 100 + 25$ ；
…
按照以上规律，解决下列问题：

(1)、填空： $7 5^{2} = 75 \times 75 =$ =；

(2)、已知 $1 \leq n \leq 9$ 且n为整数，猜想第n个等式（用含n的等式表示），并证明．

查看试题解析
22. 鱼塘承包户小李在春天往鱼塘投放了2000条鱼苗，打算在中秋节前全部售出，据统计，鱼的存活率约为 $90 %$ ．小李随机捕捞了20条鱼，将每条鱼称重后得到的质量作为一个样本，然后把鱼又放回鱼塘．统计结果如图所示：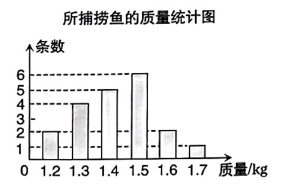

(1)、求样本的中位数和平均数；

(2)、已知这种鱼的售价为25元 $/ k g$ ，利用样本平均数，估计小李售完鱼塘里的这种鱼的总收入．

查看试题解析
23. 某中学举行校庆活动，使用了两架小型无人机进行现场拍摄，1号机所在高度 $y_{1} (m)$ 与上升时间 $x (s)$ 的函数图象如图所示；2号机从 $6 m$ 高度，以 $0.5 m / s$ 的速度上升．两架无人机同时起飞，设2号机所在高度为 $y_{2} (m)$ ．

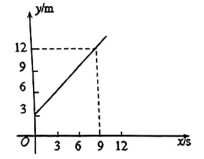(1)、求1号机所在高度 $y_{1}$ 与上升时间x之间的函数表达式（不必写出x的取值范围），并在图中画出2号机所在高度 $y_{2} (m)$ 与上升时间 $x (s)$ 的函数关系图象；

(2)、在某时刻两架无人机能否位于同一高度？如果能，求此时两架无人机的高度；如果不能，请说明理由．

查看试题解析
24. 如图1，某玩具风车的支撑杆 $O E$ 垂直于桌面 $M N$ ，点O为风车中心， $O E = 26 c m$ ，风车在风吹动下绕着中心O旋转，叶片端点A ， B ， C ， D将 $⊙ O$ 四等分，已知 $⊙ O$ 的半径为 $10 c m$ ．

(1)、风车在转动过程中，当 $∠ A O E = 45 °$ 时，点A在 $O E$ 左侧，如图2所示，求点A到桌面 $M N$ 的距离（结果保留根号）；

(2)、在风车转动一周的过程中，求点A到桌面的距离不超过 $21 c m$ 时，点A所经过的路径长（结果保留 $π$ ）；

(3)、连接 $C E$ ，当 $C E$ 与 $⊙ O$ 相切时，求切线长 $C E$ 的值，并直接写出A ， C两点到桌面 $M N$ 的距离的差．

查看试题解析
25. 图1为某游乐场过山车的一部分滑道设施，为研究过山车沿滑道运动中的数学知识，小李使用电脑软件将这部分滑道抽象出如图2所示的函数图象，并模拟过山车（抽象为点）的运动．线段 $A B$ 是一段直滑道，点A在y轴上，且 $O A = 1$ ．滑道 $B - C - D$ 为抛物线： $y = \frac{1}{4} x^{2} + b x + c$ 的一部分，在点 $C (4, 2)$ 处达到最低，点B ， D到x轴的距离相等，其中点B到点A的水平距离为2， $B G ⊥ x$ 轴于点G ．滑道 $B - C - D$ 与滑道 $D - E - F$ 可看作形状相同、开口方向相反的两段抛物线，点 $F (12, 0)$ ．

(1)、求抛物线 $B - C - D$ 和 $D - E - F$ 的函数表达式；

(2)、当过山车沿滑道从点A运动到点F的过程中，过山车到x轴的距离为1.5时，求它到出发点A的水平距离；

(3)、点M为 $B - C$ 上的一点，求点M到 $B G$ 和到x轴的距离之和（图中 $M H + M N$ ）的最大值及此时点M的坐标．

查看试题解析
26. 在 $△ A B C$ 中， $∠ A C B = 90 °$ ， $B C = 3$ ， $A C = 4$ ，点P是 $A B$ 的中点，M在 $A C$ 上（不与点C重合），连接 $P M$ ，在 $P M$ 的左侧作矩形 $P M Q N$ ．

(1)、如图1，当点N在线段 $B C$ 上时，
①若 $A M = 2$ ，求 $P N$ 的长；
②求 $t a n ∠ P N M$ 的值．

(2)、如图2，当 $P N = P M$ 时，
①若矩形 $P M Q N$ 在 $△ A B C$ 内部（包括边界），设 $A M = x$ ，写出 $C Q$ 的长与x的函数关系式，并求x的取值范围；
②若矩形 $P M Q N$ 的两个顶点落在 $△ P C A$ 的同一条边上，直接写出 $A C$ 在矩形 $P M Q N$ 内部的线段长．

查看试题解析