吉林省长春市长春汽车经济技术开发区2024年中考一模数学试题

试卷更新日期：2024-04-26 类型：中考模拟

进入出卷网下载

一、选择题(本大题共8小题，每小题 3分，共24分)

1. 计算(-3)×(-4)的结果是( )

A、-7 B、-12 C、7 D、12

查看试题解析
2. 奥迪一汽新能源汽车有限公司已全面进入预批量生产，预计今年年底实现量产，届时年产能将超过 150 000 辆.将150 000 这个数用科学记数法表示为( )

A、 $15 \times 10^{4}$ B、 $1.5 \times 10^{5}$ C、 $1.5 \times 10^{6}$ D、 $0.15 \times 10^{6}$

查看试题解析
3. 下列图形中，是长方体表面展开图的是（）

A、 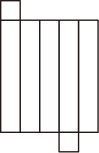B、 C、 D、

查看试题解析
4. 已知正整数a、b满足等式 $\sqrt{2} + \sqrt{a} = b \sqrt{2},$ 下列各组数值中符合要求的是( )

A、a=1，b=1 B、a=1，b=2 C、a=2，b=2 D、a=4，b=2

查看试题解析
5. 用尺规作图，已知三边作三角形，用到的基本作图是（　　）

A、作一个角等于已知角 B、作已知直线的垂线 C、作一条线段等于已知线段 D、作角的平分线

查看试题解析
6. 如图，一个零刻度落在点 A 的量角器(半圆O)的直径为 AB，等腰直角三角尺的一顶点与点 B 重合，它的斜边 BQ与半圆交于点C，直角边 BP 与半圆交于点 D.若点 C 在量角器上的读数为26°，则点 D 在量角器上的读数为（）

A、58° B、71° C、103° D、116°

查看试题解析
7. 某路灯示意图如图所示，它是轴对称图形，若∠ACB=130°，AC=BC=1.2m，CD 与地面垂直且CD=6m，则灯顶 A 到地面的高度为（）

A、 $(6 + 1.2 s i n 25 °) m$ B、 $(6 + 1.2 c o s 25 °) m$ C、 $(6 + \frac{1.2}{s i n 25 °}) m$ D、 $(6 + \frac{1.2}{c o s 25 °}) m$

查看试题解析
8. 如图，点 A 在函数 $y = \frac{4}{x} (x < 0)$ 的图象上，点 B在函数 $y = - \frac{6}{x} (x⟩ 0)$ 的图象上，AB与y轴交于点 C，D 是x轴上一点，连结 AD、BD、CD.若 AB∥x轴，则△ACD与△BCD 的面积比为（）

A、 $\frac{2}{5}$ B、 $\frac{2}{3}$ C、 $\frac{3}{2}$ D、 $\frac{4}{9}$

查看试题解析

二、填空题(本大题共 6 小题，每小题 3 分，共18 分)

9. 分解因式：a²-9= ．

查看试题解析
10. 若关于x的一元二次方程 $x^{2} + 4 x + m = 0$ 有两个不相等的实数根，则 m 的取值范围为.

查看试题解析
11. 某学校计划购买甲、乙两种品牌的电子白板共20台.甲、乙两种品牌电子白板的单价分别为3万元/台和2万元/台.若购买甲品牌电子白板费用为3(10+x)万元，则购买乙品牌电子白板费用为万元.(用含 x的代数式表示)

查看试题解析
12. 如图，扇形的半径 OA=2，∠AOB=90°，C 是 $\hat{A B}$ 上一点，CD⊥OA，CE⊥OB，垂足分别为点 D、E.若 CD=CE，则图中阴影部分图形的面积为.(结果保留π)

查看试题解析
13. 如图，在四边形 ABCD 中，AB=6，AD=4，BC=2，CD=10，则对角线 BD 的长度可能是.(写出一个即可)

查看试题解析
14. 公园要建造圆形的喷水池如图①，水面中心O处垂直于水面安装一个柱子，柱子顶端处的喷头向外喷水，水流在各个方向沿形状相同的抛物线落下.安装师傅调试发现，喷头上下移动时，抛物线形水柱随之竖直上下平移，水柱落点与点 O在同一水平面.如图②，喷头高5m时，水柱落点距O点5m；喷头高8m时，水柱落点距O点6m.现要使水柱落点距O点8m，则喷头高应调整为m.

查看试题解析

三、解答题(本大题共 10 小题，共 78分)

15. 先化简，再求值： ${(a - 1)}^{2} + a (a + 2),$ 其中 $a = \sqrt{5} .$

查看试题解析
16. 为贯彻教育部《大中小学劳动教育指导纲要(试行)》文件精神，汽开区教育局鼓励在校内“学校种植园”开展“活动+劳动教育”课程.某班决定每位学生随机抽取一张卡片来确定自己的种植项目，老师提供3张背面完全相同的卡片，其中正面分别印有白菜、辣椒、茄子图案.把这 3张卡片背面朝上洗匀，小明随机抽取一张，记录后背面朝上放回，重新洗匀后，小华再从中随机抽取一张.请用画树状图(或列表)的方法，求小明和小华抽出的卡片上的图案都是“白菜”的概率.

查看试题解析
17. “竹外桃花三两枝，春江水暖鸭先知”.为了使春天来长白山旅游的客人能够买到中华秋沙鸭玩偶，某手工作坊计划制作 600个“秋沙鸭”玩偶，为了尽快完成任务，实际平均每天完成的数量是原计划的 1.2 倍，结果提前2 天完成任务.问原计划平均每天制作多少个玩偶?

查看试题解析
18. 如图，延长 $▱ A B C D$ 的边 AB 到点 E，使 $B E = B C,$ ，延长边 CD 到点 F，使 $D F = D A,$ 连结AF、CE.求证：四边形 AECF 是平行四边形.

查看试题解析
19. 某校为更好地开展安全教育活动，随机抽取了一部分学生进行问卷调查，每名被调查的学生从防溺水、防交通事故、防食物中毒、防校园欺凌及其他各种安全意识薄弱项目中选择一项，根据调查结果，绘制出两幅不完整的统计图.

(1)、求这次被调查的学生人数.

(2)、补全条形统计图.

(3)、请估计该校 1 800名学生中防溺水意识薄弱的学生人数.

查看试题解析
20. 图①、图②、图③均是6×6的正方形网格，每个小正方形的顶点称为格点.△ABC的顶点均在格点上，M是AB 与网格线的交点，只用无刻度的直尺，分别在给定的网格中按下列要求作图，保留作图痕迹.

(1)、在图①中，作△DBC，使△DBC与△ABC全等.

(2)、在图②中，作点M关于BC的对称点 N.

(3)、在图③中，在C边上找一点E，连结 ME，使 ME=MB.

查看试题解析
21. 甲、乙两名运动员进行长跑训练，两人距终点的路程y(米)与跑步时间x(分)之间的函数关系如图所示.(0≤x≤12)

(1)、求甲距离终点的路程y(米)和跑步时间x(分)之间的函数关系式.

(2)、求甲、乙两人相距最远时的距离.

查看试题解析
22.

(1)、【感知】如图①，在正方形ABCD 内部作等边三角形PBC，连结 PA、PD，则∠APD的大小为度.

(2)、【迁移】小明遇到这样一个问题：如图，在△ABC 中，∠BAC=90°，AB=AC，点 D 是△ABC内的一点，且CD=AD，BD=BA，求证：∠ABC=3∠DBC.
小明发现，将图②通过做辅助线，变化成和图①类似，就可以求出， $∠ D B A = 30 °,$ 进而得证.下面是小明的部分证明过程：
证明：过点B作AC 的平行线，过点C 作AB 的平行线，两平行线交于点 E，连结 DE.
∵BE∥AC，CE∥AB，∴四边形 ABEC是平行四边形.
∵AB=AC，∠BAC=90°，∴四边形 ABEC是正方形.
∵DC=DA，∴∠DCA=∠DAC.
∵四边形 ABEC是正方形，∴EC=AB=BE，∠ECA=∠BAC=∠ABE=90°.
∴∠ECA-∠DCA=∠BAC--∠DAC，即∠ECD=∠BAD.
∵CD=AD，EC=AB，∴△ECD≌△BAD(S. A. S.).
∴ED=BD.
请你补全余下的证明过程.

(3)、【拓展】如图③，在 Rt△ABC中，A $C = B C = 3, ∠ A C B = 90 °, C D = 2 B D, C F ⊥ A L$ D于点E，交 AB 于点F，则 BF的长为.

查看试题解析
23. 如图，在 $R t △ A B C$ 中， $∠ C = 90 °, A B = 10, A C = 8 .$ 动点 P 从点 A 出发，沿 AB 以每秒4个单位长度的速度向终点 B 运动.过点 P 作. $P Q ⊥ A B$ 交边AC 或边 BC 于点Q，且点 P 不与点A、B重合，点 Q不与点C 重合.设线段 PQ的中点为O，将 PQ 截. $△ A B C$ 得到的小三角形绕点O 旋转 $180 °,$ 得到 $△ P Q M .$ 设 P 点的运动时间为t秒.

(1)、求 BC的长.

(2)、用含 t 的代数式表示线段CQ 的长.

(3)、当点 Q在边AC 上时，连结 BM，求线段 BM的最小值.

(4)、在点 P 运动过程中，直接写出射线 CM平分 $△ A B C$ 面积时t的值.

查看试题解析
24. 在平面直角坐标系中，抛物线 $y = x^{2} + b x + 2$ 经过点(4，2).点 P 在这条抛物线上，且点 P 的横坐标为m，过点 P 作 PQ⊥y轴，点 Q 的横坐标为2-4m.

(1)、求该抛物线所对应的函数表达式及顶点坐标.

(2)、作以 P 为圆心、半径长为3的⊙P，当⊙P与x轴相切时，求点 P 的坐标.

(3)、当线段 PQ被抛物线分成1：2 两部分时，求 m的值.

(4)、过点 P 作 $P M ⊥ x$ 轴，点 M 的纵坐标为m+2，且点 M 与点 P 不重合，连结 MQ，当抛物线在△PQM内的部分对应的函数值y随x 的增大而减小时，直接写出m的取值范围.

查看试题解析