吉林省白城市镇赉县2023-2024学年九年级下学期第一次月考数学试题
试卷更新日期:2024-04-26 类型:月考试卷
一、选择题(每小题2分,共12分)
-
1. 如图,将平面图形绕轴旋转一周,可得到的立体图形是( )
 A、
A、 B、
B、 C、
C、 D、
D、 2. 下列计算正确的是( )A、 B、 C、 D、3. 如图数学符号中,既是轴对称图形又是中心对称图形的是( )A、
2. 下列计算正确的是( )A、 B、 C、 D、3. 如图数学符号中,既是轴对称图形又是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 4. 世卫组织宣布某种病毒最大直径约为 , 将0.00000012用科学记数法表示为( )A、 B、 C、 D、5. 如图,剪两张对边平行的纸条,随意交叉叠放在一起,重合部分构成一个四边形 , 其中一张纸条在转动过程中,下列结论一定成立的是( )
4. 世卫组织宣布某种病毒最大直径约为 , 将0.00000012用科学记数法表示为( )A、 B、 C、 D、5. 如图,剪两张对边平行的纸条,随意交叉叠放在一起,重合部分构成一个四边形 , 其中一张纸条在转动过程中,下列结论一定成立的是( )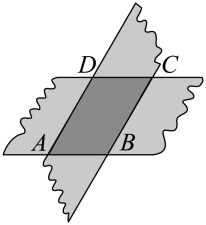 A、四边形周长不变 B、 C、四边形面积不变 D、6. 如图,已知 , 为边上一点, , 为线段的中点,以点为圆心,以线段的长为半径作弧,交于点 , 连接 , 则的长是( )
A、四边形周长不变 B、 C、四边形面积不变 D、6. 如图,已知 , 为边上一点, , 为线段的中点,以点为圆心,以线段的长为半径作弧,交于点 , 连接 , 则的长是( ) A、5 B、 C、 D、
A、5 B、 C、 D、二、填空题(每小题3分,共24分)
-
7. 计算:.8. 已知方程 , 则.9. 关于 的不等式组中的两个不等式的解集如图所示,则该不等式组的解集为.
 10. 如图,在一束平行光线中插入一张对边平行的纸板,如果光线与纸板右下方所成的角 , 则光线与纸板左上方所成的角的度数是.
10. 如图,在一束平行光线中插入一张对边平行的纸板,如果光线与纸板右下方所成的角 , 则光线与纸板左上方所成的角的度数是. 11. 如图,正六边形内接于 , 若的周长等于 , 则正六边形的边长为.
11. 如图,正六边形内接于 , 若的周长等于 , 则正六边形的边长为. 12. 如图,在中,点 , 分别在上, , , 则与的面积比为.
12. 如图,在中,点 , 分别在上, , , 则与的面积比为. 13. 如图,矩形的对角线交于点 , 分别以点 , 为圆心,以的长为半径画弧,分别交于点.若 , 则图中阴影部分的面积为.(结果保留)
13. 如图,矩形的对角线交于点 , 分别以点 , 为圆心,以的长为半径画弧,分别交于点.若 , 则图中阴影部分的面积为.(结果保留) 14. 如图,传送带的一个转动轮的半径为 , 如果转动轮绕着它的轴心转时,传送带上的物品被传送(在传送过程中物品无滑动),则.
14. 如图,传送带的一个转动轮的半径为 , 如果转动轮绕着它的轴心转时,传送带上的物品被传送(在传送过程中物品无滑动),则.
三、解答题(每小题5分,共20分)
-
15. 先化简,再求值: , 其中.16. 某商场根据市场需求,采购了两种型号扫地机器人.已知型每个进价比型的2倍少400元.采购相同数量的两种型号扫地机器人,分别用了96000元和168000元.请问两种型号扫地机器人每个的进价分别为多少元?17. 如图,甲、乙是两个可以自由转动的转盘,转盘均被分成三个面积相等的扇形,每个扇形中都标有相应的数字,指针的位置固定.同时转动两个转盘,请利用画树状图或列表的方法求甲、乙转盘停止后指针所指向的数字之和为奇数的概率.(当指针指在边界线上时视为无效,需重新转动转盘)
 18. 如图, , 点在止,且.求证:.
18. 如图, , 点在止,且.求证:.
四、解答题(每小题7分,共28分)
-
19. 如图,在正方形网格中,的顶点在格点上,请仅用无刻度的直尺完成以下作图(保留作图痕迹).
 (1)、在图①中,作关于点对称的;(2)、在图②中,作绕点顺时针旋转一定角度后,顶点仍在格点上的.20. 如图,吊车在水平地面上吊起货物时,吊绳与地面保持垂直,吊臂与水平线的夹角为 , 吊臂底部距地面.(结果精确到.参考数据:)
(1)、在图①中,作关于点对称的;(2)、在图②中,作绕点顺时针旋转一定角度后,顶点仍在格点上的.20. 如图,吊车在水平地面上吊起货物时,吊绳与地面保持垂直,吊臂与水平线的夹角为 , 吊臂底部距地面.(结果精确到.参考数据:) (1)、当吊臂底部与货物的水平距离为时,吊臂的长约为;(2)、如果该吊车吊臂的最大长度为 , 那么从地面上吊起货物的最大高度是多少米?(吊钩的长度与货物的高度忽略不计)21. 某校为了解七、八年级学生一分钟跳绳情况,从这两个年级各随机抽取50名学生进行测试,并对测试成绩(一分钟跳绳次数)进行整理、描述和分析,下面给出了部分信息:
(1)、当吊臂底部与货物的水平距离为时,吊臂的长约为;(2)、如果该吊车吊臂的最大长度为 , 那么从地面上吊起货物的最大高度是多少米?(吊钩的长度与货物的高度忽略不计)21. 某校为了解七、八年级学生一分钟跳绳情况,从这两个年级各随机抽取50名学生进行测试,并对测试成绩(一分钟跳绳次数)进行整理、描述和分析,下面给出了部分信息:
七、八年级学生一分钟跳绳成绩分析表
年级
平均数
中位数
众数
七
116
115
八
119
126
117
七年级学生一分钟跳绳成绩(数据分7组: , , , )在这一组的是:
100 101 102 103 105 106 108 109 109 110 110 111 112 113
115 115 115 116 117 119
根据以上信息,回答下列问题:
(1)、表中;(2)、在这次测试中,七年级甲同学的成绩为122次,八年级乙同学的成绩为125次,在各自年级所抽取的50名同学中,他们的测试成绩排名更靠前的是(选填“甲”或“乙”),理由是.(3)、该校七年级共有500名学生,估计一分钟跳绳不低于116次的有多少人.22. 如图,反比例函数的图象与一次函数的图象相交于 , 两点. (1)、求反比例函数和一次函数的解析式;(2)、设直线交轴于点是轴正半轴上的一动点,过点作轴交反比例函数的图象于点 , 连接.若 , 求的取值范围.
(1)、求反比例函数和一次函数的解析式;(2)、设直线交轴于点是轴正半轴上的一动点,过点作轴交反比例函数的图象于点 , 连接.若 , 求的取值范围.五、解答题(每小题8分,共16分)
-
23. 小玲和弟弟小东分别从家和图书馆同时出发,沿同一条路相向而行.小玲开始跑步,中途改为步行,到达图书馆恰好用.小东骑自行车以的速度直接回家,两人离家的距离(单位:)关于各自离开出发地的时间(单位:)的函数图象如图所示.
 (1)、家与图书馆之间的路程为 , 小玲步行的速度为;(2)、求小东离家的距离关于时间的函数解析式,并写出自变量的取值范围;(3)、求两人相遇的时间.24. 在一次数学研究性学习中,小兵将两个全等的直角三角形纸片和拼在一起,使点与点重合,点与点重合(如图①),其中 , , , 并进行如下研究活动.
(1)、家与图书馆之间的路程为 , 小玲步行的速度为;(2)、求小东离家的距离关于时间的函数解析式,并写出自变量的取值范围;(3)、求两人相遇的时间.24. 在一次数学研究性学习中,小兵将两个全等的直角三角形纸片和拼在一起,使点与点重合,点与点重合(如图①),其中 , , , 并进行如下研究活动.活动一:将图①中的纸片沿方向平移,连接(如图②),当点与点重合时停止平移.
 (1)、【思考】图②中的四边形是平行四边形吗?请说明理由.(2)、【发现】当纸片平移到某一位置时,小兵发现四边形为矩形(如图③).求的长.(3)、活动二:在图③中,取的中点 , 再将纸片绕点按顺时针方向旋转度 , 连接(如图④).
(1)、【思考】图②中的四边形是平行四边形吗?请说明理由.(2)、【发现】当纸片平移到某一位置时,小兵发现四边形为矩形(如图③).求的长.(3)、活动二:在图③中,取的中点 , 再将纸片绕点按顺时针方向旋转度 , 连接(如图④).【探究】当平分时,探究与的数量关系,并说明理由.
六、解答题(每小题10分,共20分)
-
25. 如图,在中, , , 点从点出发以的速度运动到点停止.作交边或于点 , 以为边向右作正方形.设点的运动时间为.
 (1)、请用含的代数式表示线段的长;(2)、当点在边上时,求的值;(3)、设正方形与重叠部分图形的面积为 , 当重叠部分图形为四边形时,求关于的函数解析式.26. 如图,抛物线与轴交于点 , 与轴交于点.过点作轴的垂线为抛物线上一点,其横坐标为 , 过点作于点为直线上一点,其纵坐标为 , 连接 , 设的长度为.
(1)、请用含的代数式表示线段的长;(2)、当点在边上时,求的值;(3)、设正方形与重叠部分图形的面积为 , 当重叠部分图形为四边形时,求关于的函数解析式.26. 如图,抛物线与轴交于点 , 与轴交于点.过点作轴的垂线为抛物线上一点,其横坐标为 , 过点作于点为直线上一点,其纵坐标为 , 连接 , 设的长度为. (1)、求抛物线的函数解析式;(2)、求关于的函数解析式,并写出的取值范围;(3)、直接写出随着的增大而减小时的取值范围;(4)、直接写出当轴将分成的两部分的面积比是时的值.
(1)、求抛物线的函数解析式;(2)、求关于的函数解析式,并写出的取值范围;(3)、直接写出随着的增大而减小时的取值范围;(4)、直接写出当轴将分成的两部分的面积比是时的值.