吉林省白城市镇赉县（二中、四中、蒙中）2023-2024学年八年级下学期数学第一次月考试题

试卷更新日期：2024-04-26 类型：月考试卷

进入出卷网下载

一、选择题（本大题共10小题，每小题3分，共30分）

1. 已知 $\sqrt{a^{2}} = 1, (- \sqrt{2})^{2} = b$ ，则 $\sqrt{(a + b)^{2}} =$ （）

A、1 B、3 C、1或3 D、 $- 1$ 或 $- 3$

查看试题解析
2. 如图，在 $△ A B C$ 中， $∠ C = 90 °, A C = 3, D C = 2$ ，点 $D$ 在 $B C$ 上， $∠ B A D = ∠ B, B C$ 的长为（）

A、 $2 \sqrt{3}$ B、 $\sqrt{7} + 2$ C、 $\sqrt{13} - 2$ D、 $\sqrt{13} + 2$

查看试题解析
3. 下列各式的计算正确的是（）

A、 $\sqrt{\frac{- 4}{- 9}} = \frac{\sqrt{- 4}}{\sqrt{- 9}} = \frac{- 2}{- 3} = \frac{2}{3}$ B、 $\sqrt{4 \frac{2}{9}} = 2 \frac{1}{3} \sqrt{2}$ C、 $\sqrt{\frac{3}{4}} = 2 \sqrt{3}$ D、 $\sqrt{\frac{3}{11}} \div \sqrt{3 \frac{2}{3}} = \sqrt{\frac{3}{11} \div \frac{11}{3}} = \frac{3}{11}$

查看试题解析
4. 若xy＜0，则 $\sqrt{x^{2} y}$ 化简后的结果是（）

A、 $x \sqrt{y}$ B、 $x \sqrt{- y}$ C、 $- x \sqrt{- y}$ D、 $- x \sqrt{y}$

查看试题解析
5. 勾股定理被誉为“几何明珠”，如图是我国古代著名的“赵爽弦图"，它由4个全等的直角三角形拼成，已知大正方形面积为25，小正方形面积为1，若用 $a, b (a > b)$ 表示直角三角形的两直角边，则下列结论不正确的是（）

A、 $a^{2} + b^{2} = 25$ B、 $a + b = 5$ C、 $a - b = 1$ D、 $a b = 12$

查看试题解析
6. 如图，在边长为1的小正方形网格中， $P$ 为 $C D$ 上任意一点， $(P B + P A) (P B - P A)$ 的值为（）

A、6 B、8 C、10 D、12

查看试题解析
7. 如图，正方形Ⅰ的边长为 $a$ ，面积为12；正方形Ⅱ的边长为 $b$ ，面积为27．计算 $(b - a) \div \sqrt{3}$ 的结果为（）

A、1 B、 $- 1$ C、 $\sqrt{3}$ D、 $\frac{\sqrt{3}}{3}$

查看试题解析
8. 无盖圆柱形杯子的展开图如图所示．将一根长为 $20 c m$ 的细木筷斜放在该杯子内，木筷露在杯子外面的部分至少有（）

A、 $5 c m$ B、 $7 c m$ C、 $8 c m$ D、 $11 c m$

查看试题解析
9. 已知 $a$ 满足 $| 2024 - a | + \sqrt{a - 2023} = a$ ，则 $a - 202 4^{2} =$ （）

A、0 B、1 C、2024 D、2023

查看试题解析
10. 活动探究：我们知道，已知两边和其中一边的对角对应相等的两个三角形不一定全等．如图，已知 $△ A B C$ 中， $∠ A = 30 °, A C = 3, ∠ A$ 所对的边为 $\sqrt{3}$ ，满足已知条件的三角形有两个（我们发现其中如图的 $△ A B C$ 是一个直角三角形），则满足已知条件的三角形的第三边长为（）

A、 $2 \sqrt{3}$ B、 $2 \sqrt{3} - 3$ C、 $2 \sqrt{3}$ 或 $\sqrt{3}$ D、 $2 \sqrt{3}$ 或 $2 \sqrt{3} - 3$

查看试题解析

二、填空题（本大题共6小题，每小题4分，共24分）

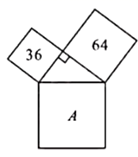
11. 已知： $\sqrt{18} - \sqrt{2} = a \sqrt{2} - \sqrt{2} = b \sqrt{2}$ ，则 $a b =$ ．

查看试题解析
12. 如图，数字代表所在正方形的面积，则A所代表的正方形的面积为.

查看试题解析
13. 如图，在等腰直角 $△ A B C$ 的斜边 $A B$ 上任取两点 $M, N$ ，使 $∠ M C N = 45 °$ ，记 $A M = m, M N = n, B N = k$ ，则以 $m, n, k$ 为边长的三角形的形状是．

查看试题解析
14. 座钟的摆针摆动一个来回所需的时间称为一个周期，其计算公式为 $T = 2 π \sqrt{\frac{l}{g}}$ ，其中 $T$ 表示周期（单位： $s$ ）， $l$ 表示摆长（单位：m）， $g = 10 m / s^{2}$ ．假若一台座钟的摆长为 $0.5 m$ ，它每摆动一个来回发出一次滴答声，那么在 $1 m i n$ 内，该座钟发出了次滴答声．（参考数据： $\sqrt{5} = 2.24, π$ 取3.14，结果保留整数）

查看试题解析
15. 先化简再求值：当 $a = - 2$ 时，求 $a + \sqrt{1 - 2 a + a^{2}}$ 的值，甲乙两人的解答如下：
甲的解答为：原式 $= a + \sqrt{(1 - a)^{2}} = a + (1 - a) = 1$ ；
乙的解答为：原式 $= a + \sqrt{(1 - a)^{2}} = a + (a - 1) = 2 a - 1 = - 5$ ．
两种解答中，的解答是错误的；
若 $a = 100$ 时， $a + \sqrt{(1 - a)^{2}} =$ ．

查看试题解析
16. 勘测队按实际需要构建了平面直角坐标系，并标示了 $A, B, C$ 三地的坐标，数据如图（单位： $k m$ ）．笔直铁路经过 $A, B$ 两地．
⑴ $A, B$ 间的距离为km．
⑵计划修一条从 $C$ 到铁路 $A B$ 的最短公路 $l$ ，并在 $l$ 上建一个维修站 $D$ ，使 $D$ 到 $A, C$ 的距离相等，则 $C, D$ 间的距离为 $k m$ ．

查看试题解析

三、解答题（共66分）

17. 计算：

(1)、 $\sqrt{6} \times \sqrt{3} - \sqrt{8}$ ；

(2)、 $\sqrt{27} \div \frac{\sqrt{3}}{2} \times 2 \sqrt{2} - 6 \sqrt{2}$ ．

查看试题解析
18. 如图，长和宽分别是 $a, b$ 的长方形纸片的四个角都剪去一个边长为 $x$ 的正方形．

(1)、用含 $a, b, x$ 的代数式表示纸片剩余部分的面积．

(2)、若 $a = 20 + 2 \sqrt{2}, b = 20 - 2 \sqrt{2}, x = \sqrt{2}$ ，求剩余部分的面积．

查看试题解析
19. 先阅读下面的一段文字，再解答问题．
已知：在平面直角坐标系中，任意两点 $M (x_{1}, y_{1}), N (x_{2}, y_{2})$ ，其两点之间的距离公式为 $M N = \sqrt{{(x_{2} - x_{1})}^{2} + {(y_{2} - y_{1})}^{2}}$ ．同时，当两点所在的直线在坐标轴上或平行于坐标轴或垂直于坐标轴时，两点之间的距离公式可以简化为 $| x_{2} - x_{1} |$ 或 $| y_{2} - y_{1} |$ ．

(1)、已知点 $A (0, 5), B (- 3, 6)$ ，试求 $A, B$ 两点之间的距离．

(2)、已知点 $A, B$ 在垂直于 $x$ 轴的直线上，点 $A$ 的坐标为 $(- 5, - \frac{1}{2})$ ， $A B = 10$ ，试确定点 $B$ 的坐标．

(3)、已知点 $A (0, 6), B (4, 0), C (- 9, 0)$ ，请判断 $△ A B C$ 的形状，并说明理由．

查看试题解析
20. 如图，在 $△ A B C$ 中， $A D ⊥ B C$ ，垂足为 $D, B D = 1, A D = 2$ ， $C D = 4$ ．

(1)、求证： $∠ B A C = 90 °$ ．

(2)、点 $P$ 为 $B C$ 上一点，连接 $A P$ ，若 $△ A B P$ 为等腰三角形，求 $B P$ 的长．

查看试题解析
21. 阅读理解材料：把分母中的根号化掉叫做分母有理化，
例如：① $\frac{1}{\sqrt{5}} = \frac{1 \times \sqrt{5}}{\sqrt{5} \times \sqrt{5}} = \frac{\sqrt{5}}{5}$ ；② $\frac{1}{\sqrt{2} - 1} = \frac{1 \times (\sqrt{2} + 1)}{(\sqrt{2} - 1) (\sqrt{2} + 1)} = \frac{\sqrt{2} + 1}{(\sqrt{2})^{2} - 1^{2}} = \sqrt{2} + 1$ 等运算都是分母有理化．
根据上述材料，解决下列问题：

(1)、化简： $\frac{1}{2 \sqrt{3}}$ ．

(2)、化简： $\frac{1}{\sqrt{5} - \sqrt{3}}$ ．

(3)、计算： $(\frac{1}{\sqrt{3} + 1} + \frac{1}{\sqrt{5} + \sqrt{3}} + \frac{1}{\sqrt{7} + \sqrt{5}} + ⋯ + \frac{1}{\sqrt{2023} + \sqrt{2021}}) \cdot (\sqrt{2023} + 1)$ ．

查看试题解析
22. 台风是一种自然灾害，它以台风中心为圆心在周圈上千米的范围内形成极端气候，有极强的破坏力．如图，有一台风中心沿东西方向 $A B$ 由点 $A$ 向点 $B$ 行驶，已知点 $C$ 为一海港．且点 $C$ 与直线 $A B$ 上两点 $A, B$ 的距离分别为 $300 k m$ 和 $400 k m$ ，又 $A B = 500 k m$ ，以台风中心为圆心周围 $250 k m$ 以内为受影响区域。

(1)、海港 $C$ 受台风影响吗？为什么？

(2)、若台风的速度为 $20 k m / h$ ，台风影响该海港持续的时间有多长？

查看试题解析
23. 如图，在长方形 $A B C D$ 中， $A B = 8, B C = 10$ ，在边 $C D$ 上取一点 $E$ ，使得将 $△ A D E$ 沿 $A E$ 折叠后点 $D$ 恰好落在 $B C$ 边上的点 $F$ 处．

(1)、求 $C E$ 的长．

(2)、在（1）的条件下， $B C$ 边上是否存在一点 $P$ ，使得 $P A + P E$ 的值最小？若存在，请求出最小值；若不存在，请说明理由．

查看试题解析