湖北省黄石市大冶市2023-2024学年八年级下学期数学期中考试试卷

试卷更新日期：2024-04-26 类型：期中考试

进入出卷网下载

一、选择题（本大题共10个小题，每小题3分，共30分）

1. $\sqrt{1 - x}$ 实数范围内有意义，则x的取值范围是（）

A、 $x > 1$ B、 $x \geq 1$ C、 $x < 1$ D、 $x \leq 1$

查看试题解析
2. 以下列各组数为边长，不能构成直角三角形的是（）

A、3，4，5 B、5，12，13 C、6，7，8 D、1， $\sqrt{2}$ ， $\sqrt{3}$

查看试题解析
3. 下列计算正确的是（）

A、 $2 \sqrt{5} - \sqrt{5} = 1$ B、 $\sqrt{3} + \sqrt{2} = \sqrt{5}$ C、 $\sqrt{8} \div \sqrt{2} = 4$ D、 $\sqrt{3} \times \sqrt{2} = \sqrt{6}$

查看试题解析
4. 下列命题中，假命题是（　　）

A、对角线互相平分的四边形是平行四边形 B、对角线互相平分且相等的四边形是矩形 C、对角线互相垂直平分的四边形是菱形 D、对角线互相垂直且相等的四边形是正方形

查看试题解析
5. 下列各式中与 $\sqrt{2}$ 是同类二次根式的是（）

A、 $\sqrt{20}$ B、 $\sqrt{\frac{1}{2}}$ C、 $\sqrt{24}$ D、 $\sqrt{0.2}$

查看试题解析
6. 在如图所示的图形中，所有四边形都是正方形，所有三角形都是直角三角形，若正方形A、C、D的面积依次为5、6、20，则正方形B的面积是（）

A、15 B、9 C、10 D、21

查看试题解析
7. 矩形具有而菱形不具有的性质是（　　）

A、对角线相等 B、对角线互相垂直 C、对角线互相平分 D、两组对角分别相等

查看试题解析
8. 如图，在 $R t △ A B C$ 中， $∠ C = 90 °$ ， D、E分别为 $C A$ 、 $C B$ 的中点， $A F$ 平分 $∠ B A C$ ，交 $D E$ 于点F，若 $A C = 6$ ， $B C = 8$ ，则 $E F$ 的长为（）

A、2 B、1 C、4 D、 $\frac{5}{2}$

查看试题解析
9. 如图，菱形 $A B C D$ 对角线 $A C = 8 c m$ ， $B D = 6 cm$ ，则菱形高 $D E$ 长为（）

A、 $5 c m$ B、 $10 c m$ C、 $4.8 c m$ D、 $9.6 c m$

查看试题解析
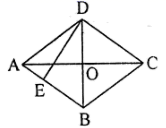10. 如图，平行四边形ABCD的对角线AC、BD相交于点O ， AE平分 $∠ B A D$ ，分别交BC、BD于点E、P ，连接OE ， $∠ A D C = 60 °$ ， $A B = \frac{1}{2} B C = 1$ ，则下列结论：① $∠ C A D = 30 °$ ② $B D = \sqrt{7}$ ③ $S_{平行四边形 A B C D} = A B \cdot A C$ ④ $O E = \frac{1}{4} A D$ ，正确的个数是（）

A、1 B、2 C、3 D、4

查看试题解析

二、填空题（本大题共5个小题，每小题3分，共15分）

11. 已知 $\sqrt{28 n}$ 为整数，则正整数n的最小值为．

查看试题解析
12. 化简： $\sqrt{(\sqrt{7} - 3)^{2}} =$ ．

查看试题解析
13. 如图，在 $▱ A B C D$ 中，BD是对角线，E ， F是对角线上的两点，要使四边形AFCE是平行四边形，还需添加一个条件（只需添加一个）是．

查看试题解析
14. 如图，在直角坐标系中，矩形ABCO的边OA在x轴上，边OC在y轴上，点B的坐标为（1，3），将矩形沿对角线AC翻折，B点落在D点的位置，且AD交y轴于点E．那么点E的坐标．

查看试题解析
15. 如图，已知矩形ABCD ， $A B = 9$ ， $A D = 4$ ， E为CD边上一点， $C E = 6$ ，点P从B点出发，以每秒1个单位的速度沿着BA边向终点A运动，连接PE ，设点P运动的时间为t秒，则当t的值为时， $△ P A E$ 是以PE为腰的等腰三角形．

查看试题解析

三、解答题（本大题共9个小题，共75分）

16. 计算：

(1)、 $\sqrt{8} - \sqrt{2} (\sqrt{2} + 2)$ ；

(2)、 $(10 \sqrt{48} - 6 \sqrt{27} + 4 \sqrt{12}) \div \sqrt{6}$ ．

查看试题解析
17. 已知 $a = 2 + \sqrt{3}$ ， $b = 2 - \sqrt{3}$ ．

(1)、直接写出： $a b =$ ， $a + b =$ ；

(2)、求 $\frac{1}{a} + \frac{1}{b}$ 的值．

查看试题解析
18. 在解决问题“已知 $a = \frac{1}{\sqrt{2} - 1}$ ，求 $3 a^{2} - 6 a - 1$ 的值”时，小明是这样分析与解答的：
$∵ a = \frac{1}{\sqrt{2} - 1} = \frac{\sqrt{2} + 1}{(\sqrt{2} - 1) (\sqrt{2} + 1)} = \sqrt{2} + 1$ ，

$∴ a - 1 = \sqrt{2}$ ，

$∴ {(a - 1)}^{2} = 2 ， a^{2} - 2 a + 1 = 2$

$∴ a^{2} - 2 a = 1$

$∴ 3 a^{2} - 6 a = 3 ， 3 a^{2} - 6 a - 1 = 2$

请你根据小明的分析过程，解决如下问题：

若 $a = \frac{2}{3 - \sqrt{7}}$ ，求 $2 a^{2} - 12 a + 1$ 的值．

查看试题解析
19. 消防车上的云梯示意图如图1所示，云梯最多只能伸长到15米，消防车高3米．如图2，某栋楼发生火灾，在这栋楼的B处有一老人需要救援，救人时消防车上的云梯伸长至最长，此时消防车的位置A与楼房的距离为12米．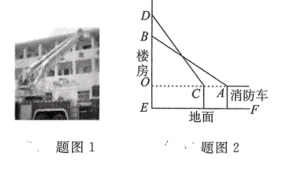

(1)、求B处与地面的距离．

(2)、完成B处的救援后，消防员发现在B处的上方3米的D处有一小孩没有及时撤离，为了能成功地救出小孩，则消防车从A处向着火的楼房靠近的距离AC为多少米?

查看试题解析
20. 如图，在 $▱ A B C D$ 中， $A E ⊥ B C$ 于点E ，延长BC至F点使 $C F = B E$ ，连接AF ， DE ， DF ．

(1)、求证：四边形AEFD是矩形；

(2)、若 $A B = 5$ ， $D E = 12$ ， $B F = 13$ ，求AE的长．

查看试题解析
21. 如图，正方形网格中的每个小正方形的边长都是1，每个小格的顶点叫做格点．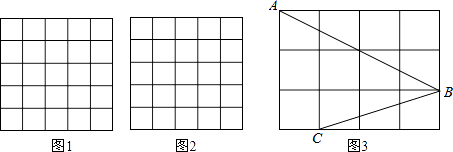

(1)、在图1中以格点为顶点画一个面积为10的正方形；

(2)、在图2中以格点为顶点画一个三角形，使三角形三边长分别为2、 $\sqrt{5}$ ， $\sqrt{13}$ ；

(3)、如图3，点A、B、C是小正方形的顶点，求∠ABC的度数．

查看试题解析
22. 如图，点D是线段AB的中点，点C是线段AB的垂直平分线上的任意点， $D E ⊥ A C$ 于点E ， $D F ⊥ B C$ 于点F ．

(1)、判断 $△ A B C$ 的形状；

(2)、求证： $C E = C F$ ；

(3)、线段CD与AB满足什么数量关系时，四边形CEDF成为正方形？请说明理由．

查看试题解析
23. 综合与实践：
综合与实践课上，老师让同学们以“正方形的折叠”为主题开展数学活动．
【操作判断】
操作一：
如图1，正方形纸片ABCD ，将 $∠ B$ 沿过点A的直线折叠，使点B落在正方形ABCD的内部，得到折痕AE ，点B的对应点为M ，连接AM；将 $∠ D$ 沿过点A的直线折叠，使AD与AM重合，得到折痕AF ，将纸片展平，连接EF ．

(1)、根据以上操作，易得点E ， M ， F三点共线，且① $∠ E A F =$ °；②线段EF ， BE ， DF之间的数量关系为．

(2)、【深入探究】操作二：如图2、将 $∠ C$ 沿EF所在直线折叠，使点C落在正方形ABCD的内部，点C的对应点为N，将纸片展平，连接NE、NF．同学们在折纸的过程中发现，当点E的位置不同时，点N的位置也不同，当点E在BC边上某一位置时（点E不与点B，C重合），点N恰好落在折痕AE上，此时AM交NF于点P，如图3所示．
小明通过观察图形，测量并猜想，得到结论 $A P = B E + D F$ ，请证明该结论是否成立，并说明理由．

(3)、【拓展应用】
若正方形纸片ABCD的边长为3，当点N落在折痕AE上时，求出线段BE的长．

查看试题解析
24. 如图，在直角坐标系中，点E为线段AB上一动点，点C为y轴上的一动点．

(1)、如图（1），若 $∠ B A O = 30 °$ ，过点E作 $E M ⊥ O A$ 于点M ，连接CM ，设 $B C = t$ ， $A E = 2 t$ ，判断四边形BCME的形状，请证明你的结论．

(2)、如图（2），过点E作 $E D ⊥ A B$ 交OA于点D ，点F在线段AO上，设 $D E = 3 t$ ， $A E = 4 t$ ，且点 $A (8, 0)$ ．
①若四边形CEFD为平行四边形，用含t的式子表示点C的坐标．
②若四边形CEFD为菱形，求t的值．

查看试题解析