湖北省黄冈市麻城市2023-2024学年九年级下学期数学期中考试试卷
试卷更新日期:2024-04-26 类型:期中考试
一、选择题:(共10题,每题3分,共30分.在每小题给出的选项中,只有一项符合
-
1. 在1, 0, , 这四个数中,最小的数是( )A、1 B、0 C、 D、2. 下列图形,是轴对称图形但不是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 把不等式组 的解集表示在数轴上,正确的是( )A、
3. 把不等式组 的解集表示在数轴上,正确的是( )A、 B、
B、 C、
C、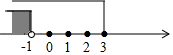 D、
D、 4. 下列计算正确的是( )A、 B、 C、 D、5. 下列说法正确的是( )A、可能性是99%的事件在一次实验中一定会发生 B、了解全国中学生
4. 下列计算正确的是( )A、 B、 C、 D、5. 下列说法正确的是( )A、可能性是99%的事件在一次实验中一定会发生 B、了解全国中学生 视力情况,采用全面调查的方式
C、了解举水河的水质情况,采用抽样调查的方式
D、从 2000 名学生中随机抽取 100 名学生进行调查,样本容量为 2000
6. 把一块直尺与一块含30°的直角三角板如图放置,若∠1=34°,则∠2的度数为( )
视力情况,采用全面调查的方式
C、了解举水河的水质情况,采用抽样调查的方式
D、从 2000 名学生中随机抽取 100 名学生进行调查,样本容量为 2000
6. 把一块直尺与一块含30°的直角三角板如图放置,若∠1=34°,则∠2的度数为( ) A、114° B、124° C、116° D、126°7. 一个正多边形的内角和为1080°,则这个正多边形的每个外角为( )A、30° B、45° C、60° D、80°8. 我们知道,四边形具有不稳定性,如图,在平面直角坐标系中,边长为2的正方形的边在x轴上,的中点是坐标原点O,固定点A,B,把正方形沿箭头方向推,使点D落在y轴正半轴上点处,则点C的对应点的坐标为( )
A、114° B、124° C、116° D、126°7. 一个正多边形的内角和为1080°,则这个正多边形的每个外角为( )A、30° B、45° C、60° D、80°8. 我们知道,四边形具有不稳定性,如图,在平面直角坐标系中,边长为2的正方形的边在x轴上,的中点是坐标原点O,固定点A,B,把正方形沿箭头方向推,使点D落在y轴正半轴上点处,则点C的对应点的坐标为( ) A、 B、 C、 D、9. 如图PA、PB是圆O的切线,切点分别为A、B,点C在AB上,过C作圆O的切线分别交PA、PB于点D、E,连接OD、OE,若∠P=50°,则∠DOE的度数为( )
A、 B、 C、 D、9. 如图PA、PB是圆O的切线,切点分别为A、B,点C在AB上,过C作圆O的切线分别交PA、PB于点D、E,连接OD、OE,若∠P=50°,则∠DOE的度数为( ) A、130° B、50° C、60° D、65°10. 在平面直角坐标系xOy中,O为坐标原点,抛物线 的对称轴为 与x轴的一个交点位于 , 两点之间.下列结论:其中正确的是( )A、 B、 C、 D、若、为方程 的两个根,则
A、130° B、50° C、60° D、65°10. 在平面直角坐标系xOy中,O为坐标原点,抛物线 的对称轴为 与x轴的一个交点位于 , 两点之间.下列结论:其中正确的是( )A、 B、 C、 D、若、为方程 的两个根,则二、填空题: (共5题, 每题3分, 共 15分
-
11. 计算: .12. 已知某一次函数的图象经过点 , 且函数y的值随自变量x的增大而减小,请写出一个符合上述条件的函数关系式: .13. “二十四节气”是上古农耕文明的智慧结晶,被国际气象界誉为“中国第五大发明”.若要从“二十四节气”主题邮票中的“立春”“芒种”“秋分”“大寒”四张邮票中随机抽取两张,则恰好抽到“芒种”和“秋分”两张邮票的概率是 .14. 桔槔俗称“吊杆”“称杆”(如图1),是我国古代农用工具,是一种利用杠杆原理的取水机械,桔槔示意图如图2所示,是垂直于水平地面的支撑杆,米,是杠杆,米, , 当点A位于最高点时, , 此时,点A到地面的距离为 .
 15. 将矩形的边向折叠,使点B恰好落在边上,记为点 , 将边向着 折叠,使点D恰好落在 上, 记为点 . 两次折痕分别为 , 若 , 两次落点的距离 , 则矩形的面积为 .
15. 将矩形的边向折叠,使点B恰好落在边上,记为点 , 将边向着 折叠,使点D恰好落在 上, 记为点 . 两次折痕分别为 , 若 , 两次落点的距离 , 则矩形的面积为 .
三、解答题:(本题共9小题,共 75分.解答应写出文字说明,证明过程或演算步骤
-
16. 计算: .17. 如图,在 中, 于点E,延长 至F点,使 ,连接 .求证:四边形 是矩形.
 18. 在大城市,很多上班族选择“低碳出行”,电动车和共享单车成为他们的代步工具.某人去距离家8千米的单位上班,骑共享单车虽然比骑电动车多用20分钟,但却能强身健体,已知他骑电动车的速度是骑共享单车的1.5倍,求骑共享单车从家到单位上班花费的时间.
18. 在大城市,很多上班族选择“低碳出行”,电动车和共享单车成为他们的代步工具.某人去距离家8千米的单位上班,骑共享单车虽然比骑电动车多用20分钟,但却能强身健体,已知他骑电动车的速度是骑共享单车的1.5倍,求骑共享单车从家到单位上班花费的时间.
19. 为了了解中学生对党史知识 知晓情况,某校开展了以“不忘初心,牢记使命”为主题的知识竞赛,现从该校八、九年级各随机抽取10名学生的成绩进行整理,描述和分析(成绩用m表示),共分成四个组:A . , B. , C . , D. . 另外给出了部分信息如下:
知晓情况,某校开展了以“不忘初心,牢记使命”为主题的知识竞赛,现从该校八、九年级各随机抽取10名学生的成绩进行整理,描述和分析(成绩用m表示),共分成四个组:A . , B. , C . , D. . 另外给出了部分信息如下:八年级10名学生的成绩: 99, 80, 99, 86, 99, 96, 90, 100, 89, 82.
九年级 10 名学生的成绩在C组的数据: 94, 90, 94.
八、九年级抽取学生成绩统计表
年级
八年级
九年级
平均数
92
92
中位数
93
b
众数
c
100
方差
52
50.4

根据以上信息,解答下列问题:
(1)、上面图表中的 , , . 扇形统计图中“D组”所对应的圆心角的度数为 .(2)、该校九年级共有840 名学生参加了知识竞赛活动,估计九年级参加此次知识竞赛活动成绩为较好的学生有多少人?(3)、根据以上信息,你认为哪个年级的学生对“不忘初心,牢记使命”的内容掌握较好? 说明理由. (一条即可)20. 如图,在平面直角坐标系中,四边形是矩形,反比例函数的图象分别与交于点和点 , 且点为的中点. (1)、求反比例函数的表达式和点的坐标;(2)、若一次函数与反比例函数的图象相交于点 , 当点在反比例函数图象上之间的部分时(点可与点重合),直接写出的取值范围.21. 如图 , 点在上,过点 , 分别与、交于、 , 过作于 .
(1)、求反比例函数的表达式和点的坐标;(2)、若一次函数与反比例函数的图象相交于点 , 当点在反比例函数图象上之间的部分时(点可与点重合),直接写出的取值范围.21. 如图 , 点在上,过点 , 分别与、交于、 , 过作于 . (1)、求证:是的切线:(2)、若与相切于点 , , , 求阴影部分面积.22. 某款旅游纪念品很受游客喜爱,每个纪念品进价40元,规定销售单价不低于44元,且不高于52元.某商户在销售期间发现,当销售单价定为44元时,每天可售出300个,销售单价每上涨1元,每天销量减少10个.现商家决定提价销售,设每天销售量为y个,销售单价为x元.(1)、写出y与x之间的函数关系式和自变量x的取值范围;(2)、将纪念品的销售单价定为多少元时,商家每天销售纪念品获得的利润w元最大?最大利润是多少元?(3)、该商户从每天的利润中捐出200元做慈善,为了保证捐款后每天剩余利润不低于2200元,求销售单价x的范围.23. 某校数学活动小组探究了如下数学问题:
(1)、求证:是的切线:(2)、若与相切于点 , , , 求阴影部分面积.22. 某款旅游纪念品很受游客喜爱,每个纪念品进价40元,规定销售单价不低于44元,且不高于52元.某商户在销售期间发现,当销售单价定为44元时,每天可售出300个,销售单价每上涨1元,每天销量减少10个.现商家决定提价销售,设每天销售量为y个,销售单价为x元.(1)、写出y与x之间的函数关系式和自变量x的取值范围;(2)、将纪念品的销售单价定为多少元时,商家每天销售纪念品获得的利润w元最大?最大利润是多少元?(3)、该商户从每天的利润中捐出200元做慈善,为了保证捐款后每天剩余利润不低于2200元,求销售单价x的范围.23. 某校数学活动小组探究了如下数学问题: (1)、问题发现:如图1,中, , . 点P是底边上一点,连接 , 以为腰作等腰 , 且 , 连接、则和的数量关系是;(2)、变式探究:如图2,中, , . 点P是腰上一点,连接 , 以为底边作等腰 , 连接 , 判断和的数量关系,并说明理由;(3)、问题解决:如图3,在正方形中,点是边上一点,以为边作正方形 , 点
(1)、问题发现:如图1,中, , . 点P是底边上一点,连接 , 以为腰作等腰 , 且 , 连接、则和的数量关系是;(2)、变式探究:如图2,中, , . 点P是腰上一点,连接 , 以为底边作等腰 , 连接 , 判断和的数量关系,并说明理由;(3)、问题解决:如图3,在正方形中,点是边上一点,以为边作正方形 , 点是正方形两条对角线的交点,连接 . 若正方形的边长为 , , 请直接写出正方形的边长.
24. 如图,在平面直角坐标系中,抛物线 与x轴交于、两点, 点D是抛物线上横坐标为6的点. 点P在这条抛物线上,且不与A、D两点重合,过点P作y轴的平行线与射线交于点 , 过点Q作垂直于y轴,点F在点Q的右侧,且 , 以、为邻边作矩形 . 设矩形的周长为 , 点的横坐标为m . (1)、求这条抛物线所对应
(1)、求这条抛物线所对应 函数表达式. (2)、求这条抛物线的对称轴将矩形的面积分为1:2 两部分时m的值.(3)、①求d与m之间的函数关系式,
函数表达式. (2)、求这条抛物线的对称轴将矩形的面积分为1:2 两部分时m的值.(3)、①求d与m之间的函数关系式,②根据d的不同取值,试探索点P的个数情况.