湖北省武汉市江岸区2023-2024学年八年级下学期期中数学考试试卷
试卷更新日期:2024-04-26 类型:期中考试
一、选择题(共10小题,每小题3分,共30分)
-
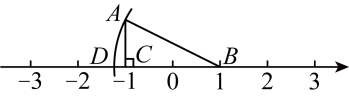
1. 若二次根式有意义,则的取值范围是( )A、 B、 C、 D、2. 下列根式是最简二次根式的是( )A、 B、 C、 D、3. 下列四组线段中,可以构成直角三角形的是( )A、1,2,3 B、2,3,4 C、5,12,13 D、4,5,64. 下列计算正确的是( )A、 B、 C、 D、5. 矩形、菱形都具有的性质是( )A、对角线互相平分 B、对角线互相垂直 C、对角线互相平分且相等 D、对角线平分一组对角6. 如图,在中, , , , 在数轴上,点B对应的数为1,以点B为圆心,的长为半径画弧,交数轴于点D , 则点D表示的数是( )
 A、 B、 C、 D、7. 如图,等腰中, , 点是底边上的一动点(不与点重合),过点分别作的平行线 , 交于点 , 则下列数量关系一定正确的是( )
A、 B、 C、 D、7. 如图,等腰中, , 点是底边上的一动点(不与点重合),过点分别作的平行线 , 交于点 , 则下列数量关系一定正确的是( )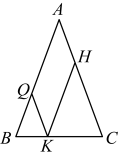 A、 B、 C、 D、8. 如图,平行四边形中,、是对角线上的两点,若添加①;②;③;④平分 , 平分中任意一个条件能够使 , 则共有几种添法( )
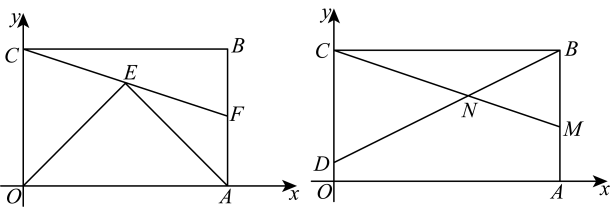
A、 B、 C、 D、8. 如图,平行四边形中,、是对角线上的两点,若添加①;②;③;④平分 , 平分中任意一个条件能够使 , 则共有几种添法( )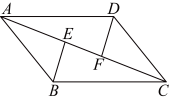 A、1 B、2 C、3 D、49. 有一个边长为1的大正方形,经过1次“生长”后,在它的左右肩上生出两个小正方形,其中三个正方形围成的三角形是直角三角形,再经过1次“生长”后,形成的图形如图1所示.如果继续“生长”下去,它将变得“枝繁叶茂”,若“生长”了2024次后形成的图形如图2所示,则图2中所有的正方形的面积和是( )
A、1 B、2 C、3 D、49. 有一个边长为1的大正方形,经过1次“生长”后,在它的左右肩上生出两个小正方形,其中三个正方形围成的三角形是直角三角形,再经过1次“生长”后,形成的图形如图1所示.如果继续“生长”下去,它将变得“枝繁叶茂”,若“生长”了2024次后形成的图形如图2所示,则图2中所有的正方形的面积和是( )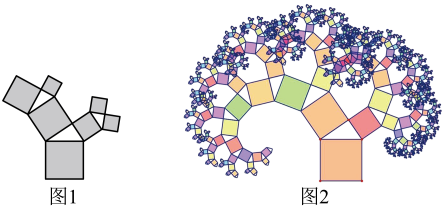 A、2025 B、2024 C、 D、10. 如图,中,对角线相交于点, , , , 则的长为( )
A、2025 B、2024 C、 D、10. 如图,中,对角线相交于点, , , , 则的长为( )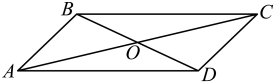 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(共6小题,每题3分,共18分)
-
11. 若最简二次根式 与 是同类二次根式,则a的值为.12. 化简: .13. 如图,菱形中,交于 , 于 , 连接 , 若 , 则的度数为°.
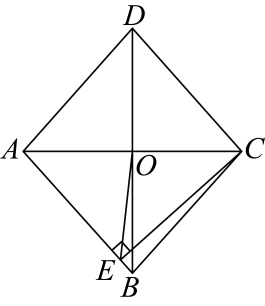 14. 某数学兴趣小组开展了笔记本电脑的张角大小的实践探究活动.如图,当张角为时,顶部边缘处离桌面的高度为 , 此时底部边缘处与处间的距离为 , 小组成员调整张角的大小继续探究,当张角时(是的对应点),则线段的长为 .
14. 某数学兴趣小组开展了笔记本电脑的张角大小的实践探究活动.如图,当张角为时,顶部边缘处离桌面的高度为 , 此时底部边缘处与处间的距离为 , 小组成员调整张角的大小继续探究,当张角时(是的对应点),则线段的长为 . 15. 如图,矩形中, , 点E为边上的一个动点,与关于直线对称.当为直角三角形时,的长为 .
15. 如图,矩形中, , 点E为边上的一个动点,与关于直线对称.当为直角三角形时,的长为 .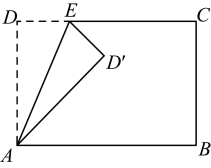 16. 四边形中,对角线 , , 点分别是的中点,连接 , 取中点 , 连接 , 则的值为 .
16. 四边形中,对角线 , , 点分别是的中点,连接 , 取中点 , 连接 , 则的值为 .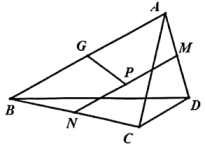
三、解答题(共8小题,共72分)
-
17. 计算(1)、(2)、18. 先化简,再求值. , 其中 .19. 如图所示,在中,点E , 点F分别是的中点,连接 .
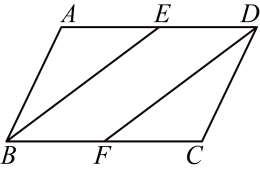 (1)、求证:四边形是平行四边形;(2)、若平分 , , 求平行四边形的周长.20. 下面是小东设计的“作矩形”的尺规作图过程.
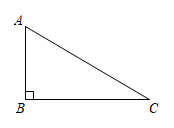
(1)、求证:四边形是平行四边形;(2)、若平分 , , 求平行四边形的周长.20. 下面是小东设计的“作矩形”的尺规作图过程.已知:Rt△ABC , ∠ABC=90°,求作:矩形ABCD .
作法:如图,①作线段AC的垂直平分线交AC于点O;
②连接BO并延长,在延长线上截取OD=OB;
③连接AD , CD .
所以四边形ABCD即为所求作的矩形.
根据小东设计的尺规作图过程.
 (1)、使用直尺和圆规,补全图形;(保留作图痕迹,下结论)(2)、为什么这样作出的四边形是矩形?请写出证明过程.21. 如图1,在每个边长为1的小正方形的网格中,点、、均在格点上.仅用无刻度的直尺在网格中完成下列画图,画图过程用虚线表示,画图结果用实线表示.
(1)、使用直尺和圆规,补全图形;(保留作图痕迹,下结论)(2)、为什么这样作出的四边形是矩形?请写出证明过程.21. 如图1,在每个边长为1的小正方形的网格中,点、、均在格点上.仅用无刻度的直尺在网格中完成下列画图,画图过程用虚线表示,画图结果用实线表示.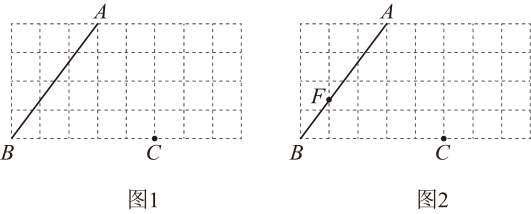 (1)、画出以为边的菱形;(2)、直接写出点到的距离;(3)、在上画点 , 使;(4)、如图2,点为与格线交点,取中点 , 连 , 在上画点 , 使 .22. 如图,平行四边形对角线交于点O , 点E在上,点F在延长线上,连接 , 且 , 与交于点G .
(1)、画出以为边的菱形;(2)、直接写出点到的距离;(3)、在上画点 , 使;(4)、如图2,点为与格线交点,取中点 , 连 , 在上画点 , 使 .22. 如图,平行四边形对角线交于点O , 点E在上,点F在延长线上,连接 , 且 , 与交于点G .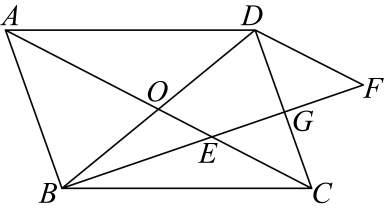 (1)、求证:;(2)、若 , , G恰好是的中点,求的长.
(1)、求证:;(2)、若 , , G恰好是的中点,求的长.