湖北省武汉市经开区2023-2024学年八年级下学期期中数学试题

试卷更新日期：2024-04-26 类型：期中考试

进入出卷网下载

一、选择题（共10小题，每小题3分，共30分）

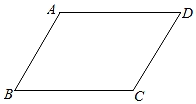
1. 式子 $\sqrt{3 - x}$ 在实数范围内有意义，则x的取值范围是（　　）

A、 $x > 3$ B、 $x ≥ 3$ C、 $x < 3$ D、 $x \leq 3$

查看试题解析
2. 下列运算正确的是（）

A、 $\sqrt{2} + \sqrt{3} = \sqrt{5}$ B、 $\sqrt{3} \times \sqrt{5} = \sqrt{15}$ C、 $\sqrt{24} \div \sqrt{6} = 4$ D、 $3 \sqrt{3} - \sqrt{3} = 3$

查看试题解析
3. 下列各组数中，是勾股数的是（）

A、1，2，3 B、3，4，5 C、 $\frac{1}{6}$ ， $\frac{1}{8}$ ， $\frac{1}{10}$ D、 $\sqrt{3}$ ， $\sqrt{4}$ ， $\sqrt{5}$

查看试题解析
4. 如图，▱ABCD中，∠B＋∠D＝100°，则∠A＝（）

A、50° B、80° C、100° D、130°

查看试题解析
5. 如图，在长方形 $A B C D$ 中，点 $E$ 是 $C D$ 上一点，连接 $A E$ ，沿直线 $A E$ 把 $△ A D E$ 折叠，使点 $D$ 恰好落在边 $B C$ 上的点 $F$ 处．若 $A B = 8, C E = 3$ ，则折痕 $A E$ 的长度为（）

A、 $5 \sqrt{3}$ B、10 C、 $5 \sqrt{5}$ D、15

查看试题解析
6. 由矩形(非正方形)各内角平分线所围成的四边形一定是(　　)

A、平行四边形 B、矩形 C、菱形 D、正方形

查看试题解析
7. 下列各命题中，原命题成立，而它逆命题不成立的是（）

A、平行四边形的两组对边分别平行 B、矩形的对角线相等 C、四边相等的四边形是菱形 D、直角三角形中，斜边的平方等于两直角边的平方和

查看试题解析
8. 我们把依次连接任意一个四边形各边中点所得的四边形叫做“中点四边形”．若一个四边形 $A B C D$ 的“中点四边形”是一个菱形，则四边形 $A B C D$ 一定满足（）

A、是菱形 B、对角线相等 C、对角线垂直 D、对角线互相平分

查看试题解析
9. 如图，在矩形 $A B C D$ 中，对角线 $A C 、 B D$ 相交于点O ， $∠ B D C = 2 ∠ A D B$ ， $A E$ 平分 $∠ B A D$ 交 $B C$ 边于点E ，点F是 $A E$ 的中点，连接 $O F ， A B = 1$ ，则 $F O$ 的长度为（　　）

A、 $\frac{\sqrt{3}}{2}$ B、 $\frac{1}{2}$ C、 $\sqrt{3} - 1$ D、 $\frac{\sqrt{3} - 1}{2}$

查看试题解析
10. 如图，四边形ABCD中，AC、BD是对角线，△ABC是等边三角形，∠ADC＝30°，AD＝4，BD＝6，则CD的长为（　　）

A、3 $\sqrt{2}$ B、4 C、2 $\sqrt{5}$ D、2 $\sqrt{13}$

查看试题解析

二、填空题（共6小题，每小题3分，共18分）

11. $\sqrt{{(- 4)}^{2}} =$ ．

查看试题解析
12. 计算： $\sqrt{18} - \sqrt{32} + 2 \sqrt{2}$ ．

查看试题解析
13. $△ A B C$ 中， $A B = 4 \sqrt{5}$ ， $A C = 5$ ，高 $A D = 4$ ，则底边 $B C$ 的长是.

查看试题解析
14. 如图一只蚂蚁从长为4cm，宽为3cm，高为2cm的长方体纸箱A点沿纸箱爬到B点，那么它爬行的最短路线的长是cm

查看试题解析
15. 如图，在正方形 $A B C D$ 中， $A B = 4$ ，点O是对角线 $A C$ 的中点，点Q是线段 $Q A$ 上的动点（点Q不与点O ， A重合），连结 $B Q$ ，并延长交边 $A D$ 于点E ，过点Q作 $F Q ⊥ B Q$ 交 $C D$ 于点F ，分别连结 $B F$ 与 $E F$ ， $B F$ 交对角线 $A C$ 于点G ，过点C作 $C H ∥ Q F$ 交 $B E$ 于点H ，连结 $A H$ ．以下四个结论：① $B Q = Q F$ ；② $△ D E F$ 周长为8；③ $∠ B Q G = ∠ B E F$ ， ④线段 $A H$ 的最小值为 $2 \sqrt{5} - 2$ ．其中正确的结论是．（填序号）

查看试题解析
16. 如图，在矩形 $A B C D$ 中， $A B = 6, A D = 10, E$ 为 $C D$ 的中点，若 $P 、 Q$ 为 $B C$ 边上的两个动点，且 $P Q = 2$ ，则线段 $A P + Q E$ 的最小值为．

查看试题解析

三、解答题（共8小题，共72分）

17. 计算：

(1)、 $(\sqrt{20} + \sqrt{18}) - (\sqrt{8} - \sqrt{125})$

(2)、 $\sqrt{8 x} - 6 \sqrt{\frac{x}{18}} + 2 x \sqrt{\frac{2}{x}}$

查看试题解析
18. 已知 $x = \frac{\sqrt{7} + \sqrt{3}}{2}, y = \frac{\sqrt{7} - \sqrt{3}}{2}$ ，求下面各代数式的值：

(1)、 $x^{2} + 3 x y + y^{2}$

(2)、 $\frac{x}{y} + \frac{y}{x}$

查看试题解析
19. 如图，在 $▱ A B C D$ 中， $B D$ 是它的一条对角线，过 $A 、 C$ 两点分别作 $A E ⊥ B D$ ， $C F ⊥ B D, E 、 F$ 为垂足．
求证：

(1)、 $D E = B F$ ．

(2)、四边形 $A F C E$ 是平行四边形．

查看试题解析
20. 已知：如图，在△ABC中，AB=13，AC=20，BC=21，AD⊥BC ，垂足为点D．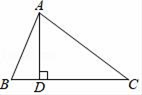

(1)、求BD、CD的长；

(2)、求△ABC的面积．

查看试题解析
21. 如图，在 $▱ A B C D$ 中， $A E ⊥ B C$ 于点E ，延长BC至F点使 $C F = B E$ ，连接AF ， DE ， DF ．

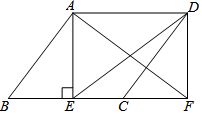(1)、求证：四边形AEFD是矩形；

(2)、若 $A B = 6$ ， $D E = 8$ ， $B F = 10$ ，求AE的长．

查看试题解析
22. 如图是由小正方形组成的 $8 \times 7$ 网格，每个边长为1的小正方形的顶点叫做格点．正方形 $A B C D$ 四个顶点都是格点．点E的坐标为 $(3, 3)$ ．仅用无刻度的直尺在给定的网格中完成画图，画图过程线用虚线，结果线用实线表示．

(1)、在图1中，以 $A E$ 为边画 $▱ A E C F$ ；

(2)、在图1中，在 $C F$ 上画点M ，使得 $B M = D P$ ；

(3)、在图2中，在 $B C$ 上画点G ，使得 $∠ E A G = 45 °$

(4)、直接写出 $G E$ 与x轴交点的横坐标；

查看试题解析
23. 在菱形 $A B C D$ 和菱形 $B E F G$ 中， $∠ A B C = ∠ E B G = 60 °, A B = 6, B E = 2$ ．

(1)、如图1，若点 $E 、 G$ 分别在边 $A B 、 B C$ 上，点F在菱形 $A B C D$ 内部，连接 $D F$ ，直接写出 $D F$ 的长度为；

(2)、如图2，把菱形 $B E F G$ 绕点B顺时针旋转 $α ° (0 < α < 360)$ ，连接 $D F 、 C G$ ，判断 $D F$ 与 $C G$ 的数量关系，并给出证明；

(3)、如图3，①把菱形 $B E F G$ 继续绕点B顺时针旋转，连接 $G D, O$ 为 $D G$ 的中点，连接 $C O 、 E O$ ，试探究 $C O$ 与 $E O$ 的关系；②直接写出菱形 $B E F G$ 绕B点旋转过程中 $C O$ 的取值范围．

查看试题解析
24. 在平面直角坐标系中，四边形 $O A C E$ 为矩形， $A (m, 0), E (0, n)$ ，连接 $A E$ ．

(1)、如图1， $A B$ 平分 $∠ C A O$ 交y轴与点B ，交 $C E$ 于点D ，直接写出点 $B 、 C 、 D$ 的坐标：
B（，）C（，）D（，）；

(2)、如图1，在（1）的条件下，F为 $B D$ 的中点，求 $∠ A E C + ∠ B O F$ 的值，并直接写出 $\frac{O F}{A E}$ 的值；

(3)、如图2，点M从O点出发沿射线 $O E$ 运动，点N从A点出发沿 $A O$ 运动， $P 、 Q$ 分别为 $E N 、 A M$ 的中点，若 $M 、 N$ 两点以相同的速度同时出发运动，当 $m = 4, n = 2$ 时，直接写出当 $E N + A M$ 有最小值时 $P Q$ 的长度．

查看试题解析