广东省佛山市三水区2023-2024学年八年级下学期数学期中考试试卷
试卷更新日期:2024-04-26 类型:期中考试
一、选择题(共12小题,每小题3分,共36分)
-
1. 下列图形中,既是中心对称图形,又是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 交通法规人人遵守,文明城市处处安全.在通过桥洞时,我们往往会看到如图所示的标志,这是限制车高的标志.则通过该桥洞的车高x(m)的范围在数轴上可表示为( )
2. 交通法规人人遵守,文明城市处处安全.在通过桥洞时,我们往往会看到如图所示的标志,这是限制车高的标志.则通过该桥洞的车高x(m)的范围在数轴上可表示为( ) A、
A、 B、
B、 C、
C、 D、
D、 3. 等腰三角形的两边长分别为3和6,则这个三角形的周长是( )A、15 B、12 C、12或15 D、94. 在平面直角坐标系中,线段是由线段经过平移得到的,已知点的对应点为 , 点的坐标为 , 则点的坐标为( )A、 B、 C、 D、5. 下列等式从左到右的变形,属于因式分解的是( )A、 B、 C、 D、6. 如图, 是由 绕点 顺时针旋转 后得到的图形,若点 恰好落在 上,且 的度数为( )
3. 等腰三角形的两边长分别为3和6,则这个三角形的周长是( )A、15 B、12 C、12或15 D、94. 在平面直角坐标系中,线段是由线段经过平移得到的,已知点的对应点为 , 点的坐标为 , 则点的坐标为( )A、 B、 C、 D、5. 下列等式从左到右的变形,属于因式分解的是( )A、 B、 C、 D、6. 如图, 是由 绕点 顺时针旋转 后得到的图形,若点 恰好落在 上,且 的度数为( )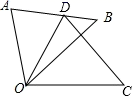 A、 B、 C、 D、7. 如图,在 中, 是 边的中点,且BD⊥AC,ED//BC,ED交AB于点E,若AC=4,BC=6,则 的周长为( )
A、 B、 C、 D、7. 如图,在 中, 是 边的中点,且BD⊥AC,ED//BC,ED交AB于点E,若AC=4,BC=6,则 的周长为( )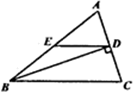 A、 B、 C、 D、8. 如图,直线与相交于点 , 若点的横坐标为 , 则关于的不等式的解集是( )
A、 B、 C、 D、8. 如图,直线与相交于点 , 若点的横坐标为 , 则关于的不等式的解集是( ) A、 B、 C、 D、9. 如图,在△ABC中,∠ABC=90°,将△ABC沿AB方向平移AD的长度得到△DEF,已EF=8,BE=3,CG=3,则图中阴影部分的面积是( )
A、 B、 C、 D、9. 如图,在△ABC中,∠ABC=90°,将△ABC沿AB方向平移AD的长度得到△DEF,已EF=8,BE=3,CG=3,则图中阴影部分的面积是( ) A、12.5 B、19.5 C、32 D、45.510. 缤纷节临近,小西在准备爱心易物活动中发现班级同学捐赠的一个布偶的成本为60元,定价为90元,为使得利润率不低于5%,在实际售卖时,该布偶最多可以打( )折.A、8 B、7 C、7.5 D、8.511. 如果不等式组的解集是x≤5,那么n的取值范围是( )A、n≤5 B、n<5 C、n>5 D、n≥512. 如图,是等边内一点, , 将线段以点为旋转中心逆时针旋转得到线段 , 下列结论:①可以由绕点逆时针旋转得到;②点与的距离为6;③;④;⑤ . 其中正确的结论有( )个
A、12.5 B、19.5 C、32 D、45.510. 缤纷节临近,小西在准备爱心易物活动中发现班级同学捐赠的一个布偶的成本为60元,定价为90元,为使得利润率不低于5%,在实际售卖时,该布偶最多可以打( )折.A、8 B、7 C、7.5 D、8.511. 如果不等式组的解集是x≤5,那么n的取值范围是( )A、n≤5 B、n<5 C、n>5 D、n≥512. 如图,是等边内一点, , 将线段以点为旋转中心逆时针旋转得到线段 , 下列结论:①可以由绕点逆时针旋转得到;②点与的距离为6;③;④;⑤ . 其中正确的结论有( )个 A、5 B、4 C、3 D、2
A、5 B、4 C、3 D、2二、填空题(本大题共6小题,每小题4分,共24分)
-
13. 因式分解: .14. 不等式的最大整数解是 .15. 如果直角三角形的两边的长分别为3、4,则斜边长为 .16. 如图,在 中, , , 的垂直平分线分别交 , 于 , , ,则 的长为.
 17. 如图,四个图形能拼成一个大长方形,据此可写出个多项式的因式分解: .
17. 如图,四个图形能拼成一个大长方形,据此可写出个多项式的因式分解: . 18. 如图,等边的周长是18,AD是BC边上的中线,M是AD上的动点,E是AC边上一点,若AE=3,EM+CM的最小值为 .
18. 如图,等边的周长是18,AD是BC边上的中线,M是AD上的动点,E是AC边上一点,若AE=3,EM+CM的最小值为 .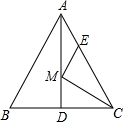
三、解答题(共6小题,19题8分,20题6分,21-22题10分,23题12分,24题14分)
-
19. 如图在△ABC中,∠A>∠B.
 (1)、作边AB的垂直平分线DE,与AB,BC分别相交于点D,E(用尺规作图,保留作图痕迹,不要求写作法);(2)、在(1)的条件下,连接AE,若∠B=55°,求∠AEC的度数.20. 解不等式组: , 并在数轴上表示解集.21. 如图,△ABC中,∠ACD = 90°,AB= 10,AC= 6,AD平分∠BAC , DE ⊥ AB , 垂足为点E .
(1)、作边AB的垂直平分线DE,与AB,BC分别相交于点D,E(用尺规作图,保留作图痕迹,不要求写作法);(2)、在(1)的条件下,连接AE,若∠B=55°,求∠AEC的度数.20. 解不等式组: , 并在数轴上表示解集.21. 如图,△ABC中,∠ACD = 90°,AB= 10,AC= 6,AD平分∠BAC , DE ⊥ AB , 垂足为点E . (1)、线段AD与CE是否垂直平分?说明理由;(2)、求△BDE的周长;(3)、求四边形AEDC的面积.22. 我市某中学计划举行以“奋斗百年路,启航新征程”为主题的知识竞赛,并对获奖的同学给予奖励.现要购买甲、乙两种奖品,已知1件甲种奖品和2件乙种奖品共需40元,2件甲种奖品和3件乙种奖品共需70元.(1)、求甲、乙两种奖品的单价;(2)、根据颁奖计划,该中学需甲、乙两种奖品共60件,且甲种奖品的数量不少于乙种奖品数量的 , 应如何购买才能使总费用最少?并求出最少费用。23. 定义一种新运算“a*b”:当a≥b时,a*b=a+2b;当a<b时,a*b=a-2b.
(1)、线段AD与CE是否垂直平分?说明理由;(2)、求△BDE的周长;(3)、求四边形AEDC的面积.22. 我市某中学计划举行以“奋斗百年路,启航新征程”为主题的知识竞赛,并对获奖的同学给予奖励.现要购买甲、乙两种奖品,已知1件甲种奖品和2件乙种奖品共需40元,2件甲种奖品和3件乙种奖品共需70元.(1)、求甲、乙两种奖品的单价;(2)、根据颁奖计划,该中学需甲、乙两种奖品共60件,且甲种奖品的数量不少于乙种奖品数量的 , 应如何购买才能使总费用最少?并求出最少费用。23. 定义一种新运算“a*b”:当a≥b时,a*b=a+2b;当a<b时,a*b=a-2b.例如:3*(-4)=3+(-8)=-5,(-6)*12=-6-24=-30
(1)、填空:(-4)*3=.(2)、若(3x-4)*(x+6)=(3x-4)+2(x+6),则x的取值范围为;(3)、已知(3x-7)*(3-2x)<-6,求x的取值范围;(4)、小明在计算(2x2-4x+8)*(x2+2x-2)时随意取了一个x的值进行计算,得出结果是-4,小丽告诉小明计算错了,问小丽是如何判断的.24. 如图1,点分别是边长为的等边的边上的动点,点从顶点 , 点从顶点同时出发,且它们的速度都为 . (1)、连接交于点 , 则在运动的过程中,变化吗?若变化,则说明理由;若不变,则求出它的度数;(2)、点在运动过程中,设运动时间为 , 当为何值时,为直角三角形?(3)、如图2,若点在运动到终点后继续在射线上运动,直线交点为 , 在运动的过程中,的大小变化吗?若变化请说明理由:若不变,请求出它的度数.
(1)、连接交于点 , 则在运动的过程中,变化吗?若变化,则说明理由;若不变,则求出它的度数;(2)、点在运动过程中,设运动时间为 , 当为何值时,为直角三角形?(3)、如图2,若点在运动到终点后继续在射线上运动,直线交点为 , 在运动的过程中,的大小变化吗?若变化请说明理由:若不变,请求出它的度数.